
J966 第二个主成分2,也应该最大化方差,变 换具有单位长度,并且与州正交。 对于第二个主成分,有 maxw∑w2-a(w5w2-1)-B(w%-0)〉 关于w2求导并令其为0,得到 2∑w2-2cw2-Bw1=0
第二个主成分 也应该最大化方差,变 换具有单位长度,并且与 正交。 对于第二个主成分,有 2 z w1 关于 w2求导并令其为0,得到

/96 上式两边乘以w得: 2w∑w2-2a'ww2-BW,=0 其中ww,=0,且w∑w是标量 w∑w2=w3∑% w∑w2=w∑W=wW=w%=0 可知B=0,并且可得∑w2=w2
上式两边乘以 1 得: T w 2 2 0 w1 w2 w1 w2 w1 w1 T T T , 其中 可知β=0 ,并且可得 w2 w2 ,
J966 这表明w,应该是∑的特征向量,具 有第二大特征值2=x 类似的,可以证明其它维被具有递减 的特征值的特征向量给出。 Scree Plot Component Number
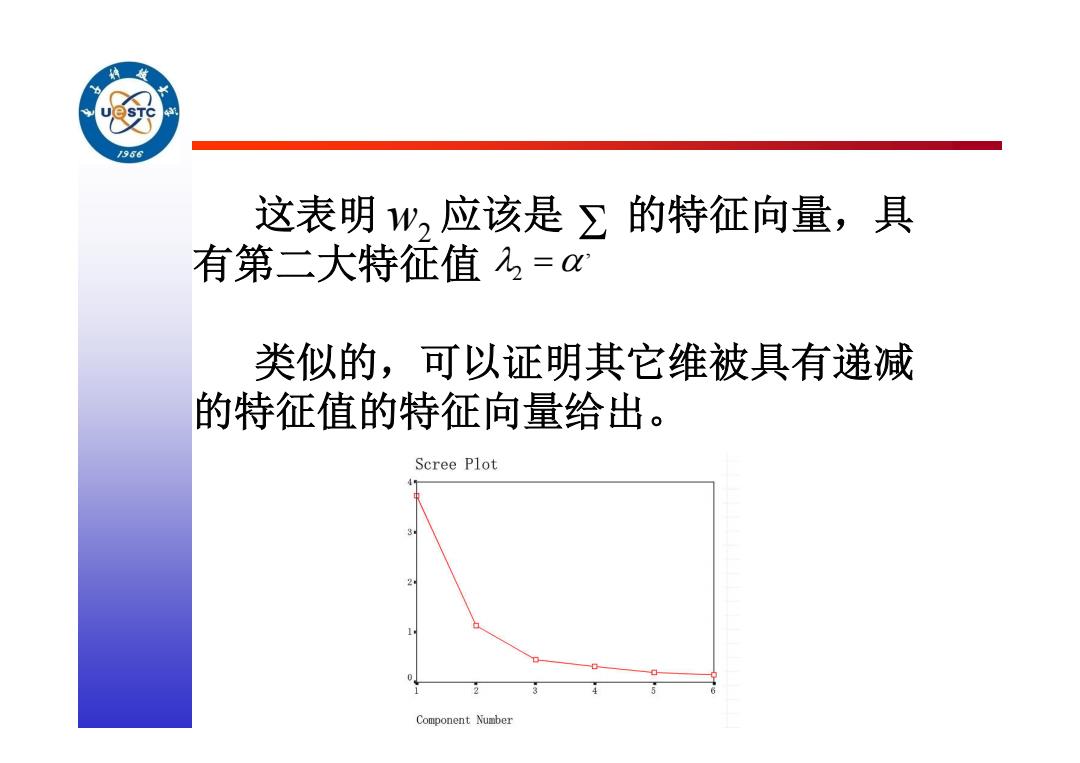
这表明 应该是 的特征向量,具 有第二大特征值 类似的,可以证明其它维被具有递减 的特征值的特征向量给出。 w2 , 2

总方差中属于主成分几的比例为 /966 称为主成分2的贡献率。 第一主成分z1的贡献率最大,表明它解释 原始变量x,x2,,x的能力最强,而31,22,,2k 的解释能力依次递减。 主成分分析的目的就是为了减少变量的 个数,因而一般是不会使用所有主成分的, 忽略一些带有较小方差的主成分将不会给总 方差带来大的影响
总方差中属于主成分 的比例为 称为主成分 的贡献率。 第一主成分 的贡献率最大,表明它解释 原始变量 的能力最强,而 的解释能力依次递减。 主成分分析的目的就是为了减少变量的 个数,因而一般是不会使用所有主成分的, 忽略一些带有较小方差的主成分将不会给总 方差带来大的影响。 i 1 i k j j i z 1 2 , ,..., n x x x 1 2 , ,..., k z z z 1 z

前k个主成分的贡献率之和 /966 j=1 称为主成分,2,,的累计贡献率,它表明 31,22,2k解释,,…,的能力。 通常取较小的k,使得累计贡献达到一个 较高的百分比(如80%一90%)。此时,, 可用来代替x,2,,x,从而达到降维的目的, 而信息的损失却不多
前k个主成分的贡献率之和 称为主成分 的累计贡献率,它表明 解释 的能力。 通常取较小的k,使得累计贡献达到一个 较高的百分比(如80%~90%)。此时, 可用来代替 ,从而达到降维的目的, 而信息的损失却不多。 1 1 k i i n j j 1 2 , ,..., k 1 2 , ,..., k z z z 1 2 , ,..., n x x x 1 2 , ,..., n x x x