
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 第四章测试系统的频率响应 一、机-电相似原理 二、灵敏系统的固有振动 三、灵敏系统的强迫振动 机械与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 第四章 测试系统的频率响应 一、机-电相似原理 二、灵敏系统的固有振动 三、灵敏系统的强迫振动

SME 机械与电气工程学院 School of Machanical and Elcetrical Engineering 测试系统的频率响应? 观点1:测试系统的输出响应应正确表示输入激励,但实际系统的响应 往往随被测信号的频率变化而变化,因此,频率响应即为测试系统极为 重要的特征。 观点2:测试系统的前端(传感器、敏感环节)是其核心部分,在力学 量测试中,由质量M弹簧K-阻尼u构成其“灵敏系统”,而且在指示仪 表/记录仪中也是重要组成部分,讨论M-K-μ灵敏系统具有典型意义。 观点3:敏感环节与能量转换环节紧密相连,构成机械-电气系统,因 此,研究机-电相似性、典型机电系统的频率响应具有普遍意义。 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 观点1:测试系统的输出响应应正确表示输入激励,但实际系统的响应 往往随被测信号的频率变化而变化,因此,频率响应即为测试系统极为 重要的特征。 观点2:测试系统的前端(传感器、敏感环节)是其核心部分,在力学 量测试中,由质量M-弹簧K-阻尼μ构成其“灵敏系统” ,而且在指示仪 表/记录仪中也是重要组成部分,讨论M-K-μ灵敏系统具有典型意义。 观点3:敏感环节与能量转换环节紧密相连,构成机械-电气系统,因 此,研究机-电相似性、典型机电系统的频率响应具有普遍意义。 测试系统的频率响应?

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 一、机-电相以原理 意义: ①根据相似原理,便于将“非电量”转换为“电量”进行测试、分析 和处理; ②研究机-电相似性,便于在设计、仿真、实测验证等方面推广应用。 机越与电气工程学院
意义: ① 根据相似原理,便于将“非电量”转换为“电量”进行测试、分析 和处理; ② 研究机-电相似性,便于在设计、仿真、实测验证等方面推广应用。 机械与电气工程学院 School of Machanical and Elcetrical Engineering 一、机-电相似原理
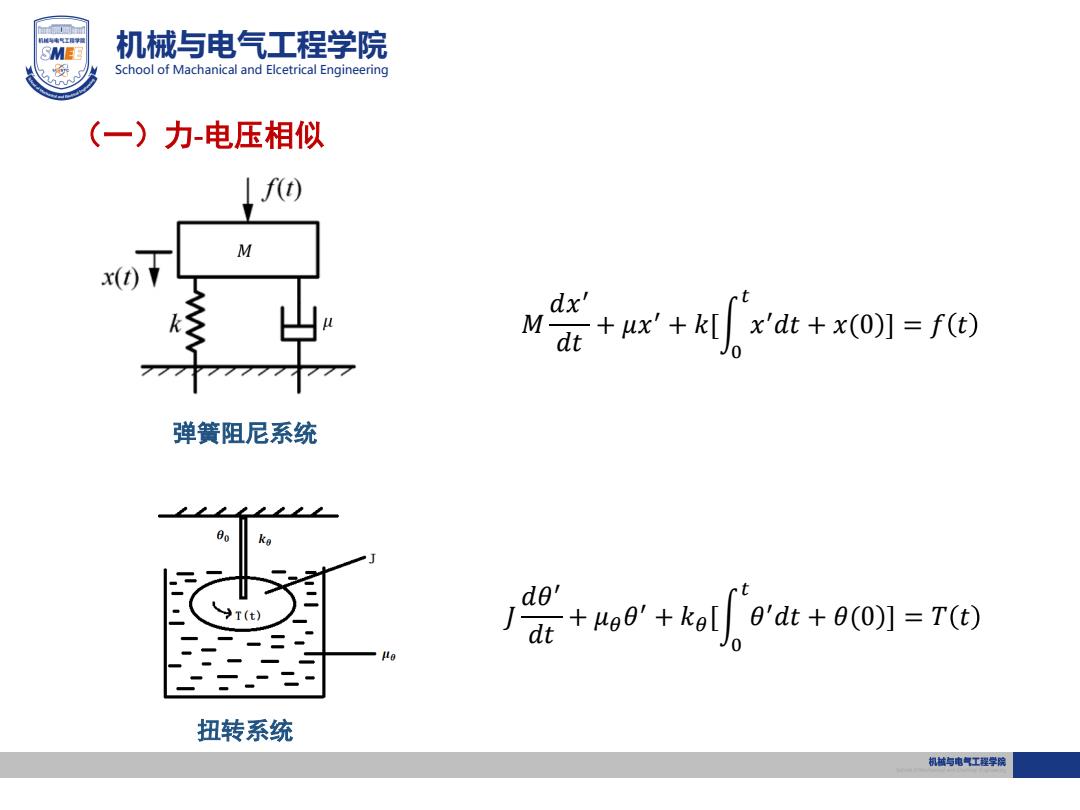
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering (一)力-电压相似 f M 货+r+rt+xo1=f阳 弹簧阻尼系统 1(t) JR+eg'+kalg0at+9o1=r 扭转系统 机械与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (一)力-电压相似 𝑀 𝑑𝑥 ′ 𝑑𝑡 + 𝜇𝑥 ′ + 𝑘[ 0 𝑡 𝑥 ′𝑑𝑡 + 𝑥(0 ] = 𝑓 𝑡 弹簧阻尼系统 扭转系统 𝐽 𝑑𝜃 ′ 𝑑𝑡 + 𝜇𝜃𝜃 ′ + 𝑘𝜃[ 0 𝑡 𝜃 ′𝑑𝑡 + 𝜃(0 ] = 𝑇 𝑡
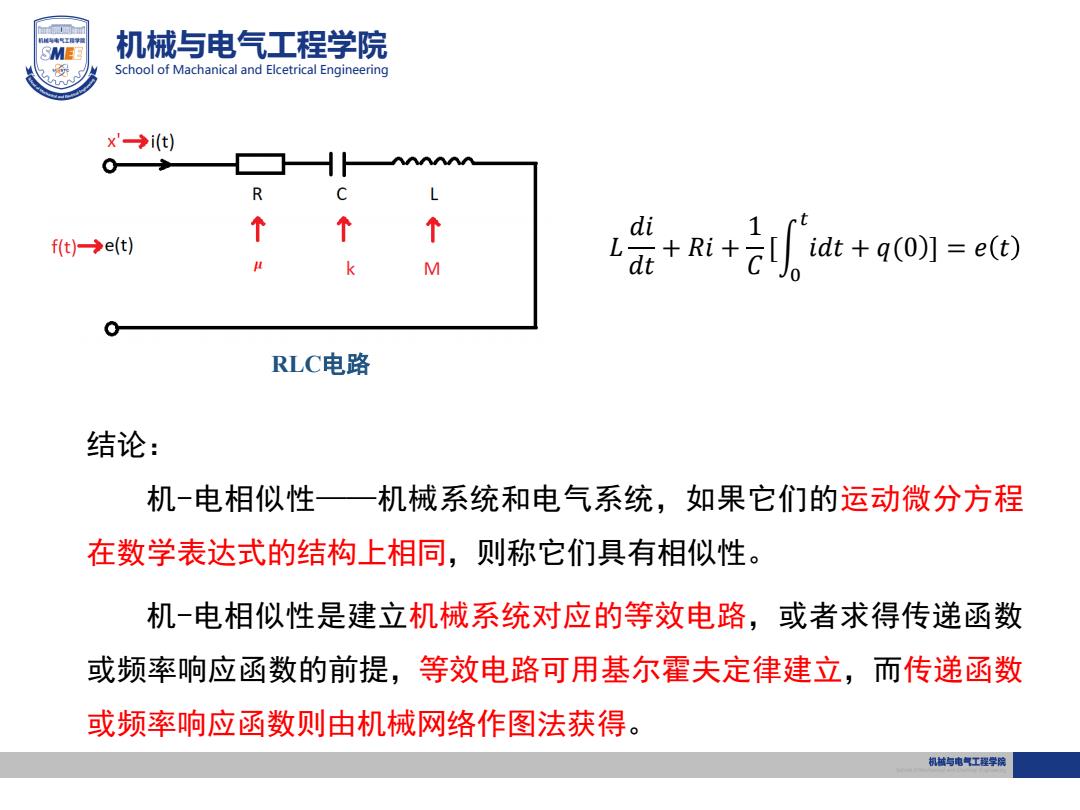
机械与电气工程学院 School of Machanical and Elcetrical Engineering x'→i(t) R C 个 ft)-→e(t) k M 张+i+2dt+go训=e0 RLC电路 结论: 机-电相似性 机械系统和电气系统,如果它们的运动微分方程 在数学表达式的结构上相同,则称它们具有相似性。 机-电相似性是建立机械系统对应的等效电路,或者求得传递函数 或频率响应函数的前提,等效电路可用基尔霍夫定律建立,而传递函数 或频率响应函数则由机械网络作图法获得。 机城与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 𝐿 𝑑𝑖 𝑑𝑡 + 𝑅𝑖 + 1 𝐶 [ 0 𝑡 𝑖𝑑𝑡 + 𝑞(0 ] = 𝑒 𝑡 RLC电路 结论: 机-电相似性——机械系统和电气系统,如果它们的运动微分方程 在数学表达式的结构上相同,则称它们具有相似性。 机-电相似性是建立机械系统对应的等效电路,或者求得传递函数 或频率响应函数的前提,等效电路可用基尔霍夫定律建立,而传递函数 或频率响应函数则由机械网络作图法获得