
投资方案风险估计一一解析法 条件:方案的经济效果指标(如净现值)服从某种典型概论分 布;期望值与标准差已知 例,假定在上例(书中142页)方案净现值服从正态分布 ,利用其计算结果求:净现值大于或等于0的概率;净现 值小于一100万元的概率;净现值大于或等于500万元的概 率。 解:若连续型随机变量X服从参数为μ,σ的正态分布,X 具有分布函数 (t-4)2 bW=2a 202 dt 吉林大学管理学院版权所有
吉林大学管理学院版权所有 2 投资方案风险估计--解析法 条件:方案的经济效果指标(如净现值)服从某种典型概论分 布;期望值与标准差已知 例,假定在上例(书中142页)方案净现值服从正态分布 ,利用其计算结果求:净现值大于或等于0的概率;净现 值小于-100万元的概率;净现值大于或等于500万元的概 率。 解:若连续型随机变量X服从参数为μ,σ的正态分布,X 具有分布函数 F x dt x t − − − = 2 2 2 ( ) 2 1 ( )

冷正山上式可化为标准正态分布函数 0-,5总m=52 x-u 令Z=X二μ 由正态分布表查出x<X的概率值 0 P(x<x)=P(Z<-兴)=D() 假设方案的净现值是连续型随机变量, u=E(NPV)=232.83(万元),o=σ(NPV)=246.39(万元)则 NPV-E(NPV) NPV-232.83 Z= (NPV) 246.39 3 吉林大学管理学院版权所有
吉林大学管理学院版权所有 3 令u= t- μ σ 上式可化为标准正态分布函数 ( ) 2 1 ( ) 2 2 − = = − − − x F x du x u 令Z= x- μ σ ,由正态分布表查出x<x0的概率值 ( ) ( ) ( ) 0 0 0 − = − = x x P x x P Z 假设方案的净现值是连续型随机变量, μ=E(NPV)=232.83(万元), σ = σ(NPV)=246.39(万元) 则 246.39 232.83 ( ) ( ) − = − = NPV NPV NPV E NPV Z

净现值大于或等于0的概率 P(NPV≥0)=1-P(NPV<0) =1-P(z< 0-232.8 )=1-P(Z<-0.9450)=P(Z<0.9450)=0.8276 246.39 净现值小于一100万元的概率 PWPV<-100)=P(Z<-100-232.83 246.39 =P(Z<-1.351)=1-P(Z<1.351)=1-0.9115=0.0885 净现值大于或等于500万元的概率 P(NPV≥500)=1-P(NPV<500) =1-Pz< 500-232.83 =1-P(Z<1.084)=1-0.8608=0.1392 246.39 正态分布条件下,μ士ō范围内的概率为68.3% u士2σ范围内的概率为95.4% u±3σ范围内的概率为99.7% 吉林大学管理学院版权所有
吉林大学管理学院版权所有 4 净现值大于或等于0的概率 ) 1 ( 0.9450) ( 0.9450) 246.39 0 232.83 1 ( ( 0) 1 ( 0) = − − = − = − = − P Z P Z P Z P NPV P NPV 净现值小于-100万元的概率 ( 1.351) 1 ( 1.351) 1 0.9115 0.0885 ) 246.39 100 232.83 ( 100) ( = − = − = − = − − − = P Z P Z P NPV P Z 净现值大于或等于500万元的概率 ) 1 ( 1.084) 1 0.8608 0.1392 246.39 500 232.83 1 ( ( 500) 1 ( 500) = − = − = − = − = − P Z P Z P NPV P NPV 正态分布条件下, μ±σ范围内的概率为68.3% μ±2σ范围内的概率为95.4% μ±3σ范围内的概率为99.7% =0.8276

投资方案风险估计一一图示法 序号 状态组合 净现值NPVO 发生概率P 累计概率 (i=12%) 1 Om3NOr1 -170.98 0.08 0.08 2 OminO2 -98.81 0.08 0.16 3 OmnO -26.71 0.04 0.20 4 Omne1 117.48 0.24 0.44 5 OmNO2 261.67 0.24 0.68 6 0m2∩Oeg 405.86 0.12 0.80 7 0m∩Oi 405.86 0.08 0.88 8 ⊙ming2 622.15 0.08 0.96 9 ⊙m1∩03 838.44 0.04 1.00 5 吉林大学管理学院版权所有
吉林大学管理学院版权所有 5 投资方案风险估计--图示法 序号 状态组合 净现值NPV(j) (i0=12%) 发生概率Pj 累计概率 1 Θm3∩Θr1 -170.98 0.08 0.08 2 Θm3∩Θr2 -98.81 0.08 0.16 3 Θm3∩Θr3 -26.71 0.04 0.20 4 Θm2∩Θr1 117.48 0.24 0.44 5 Θm2∩Θr2 261.67 0.24 0.68 6 Θm2∩Θr3 405.86 0.12 0.80 7 Θm1∩Θr1 405.86 0.08 0.88 8 Θm1∩Θr2 622.15 0.08 0.96 9 Θm1∩Θr3 838.44 0.04 1.00
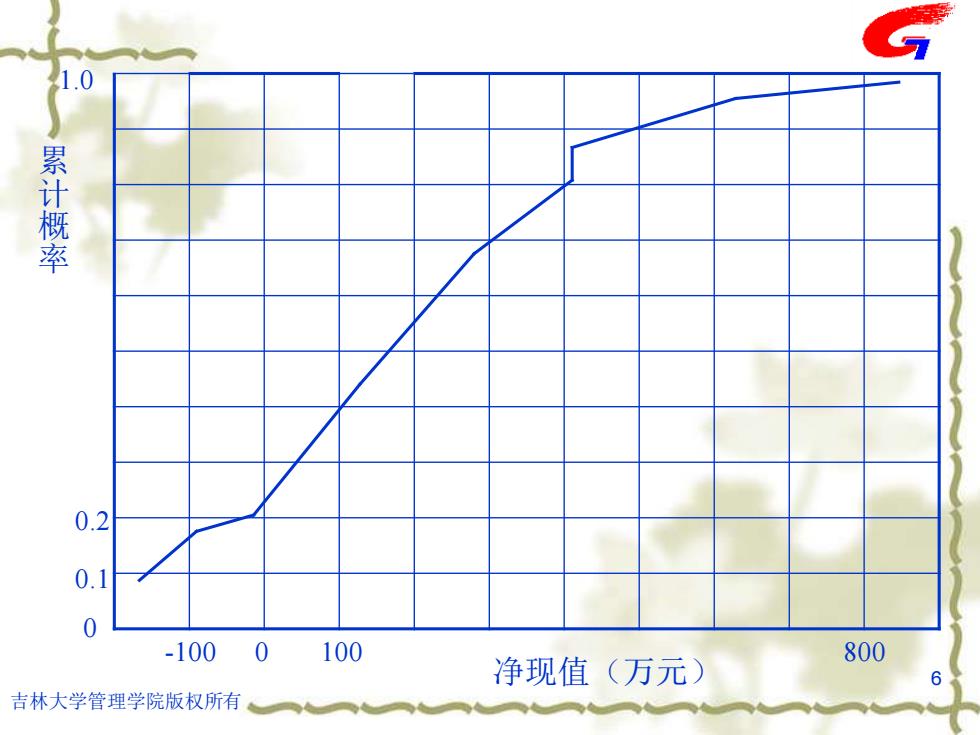
1.0 累计概率 0.2 0.1 0 -100 0 100 800 净现值(万元) 6 吉林大学管理学院版权所有
吉林大学管理学院版权所有 6 0 0.1 -100 0 100 1.0 累 计 概 率 净现值(万元) 800 0.2