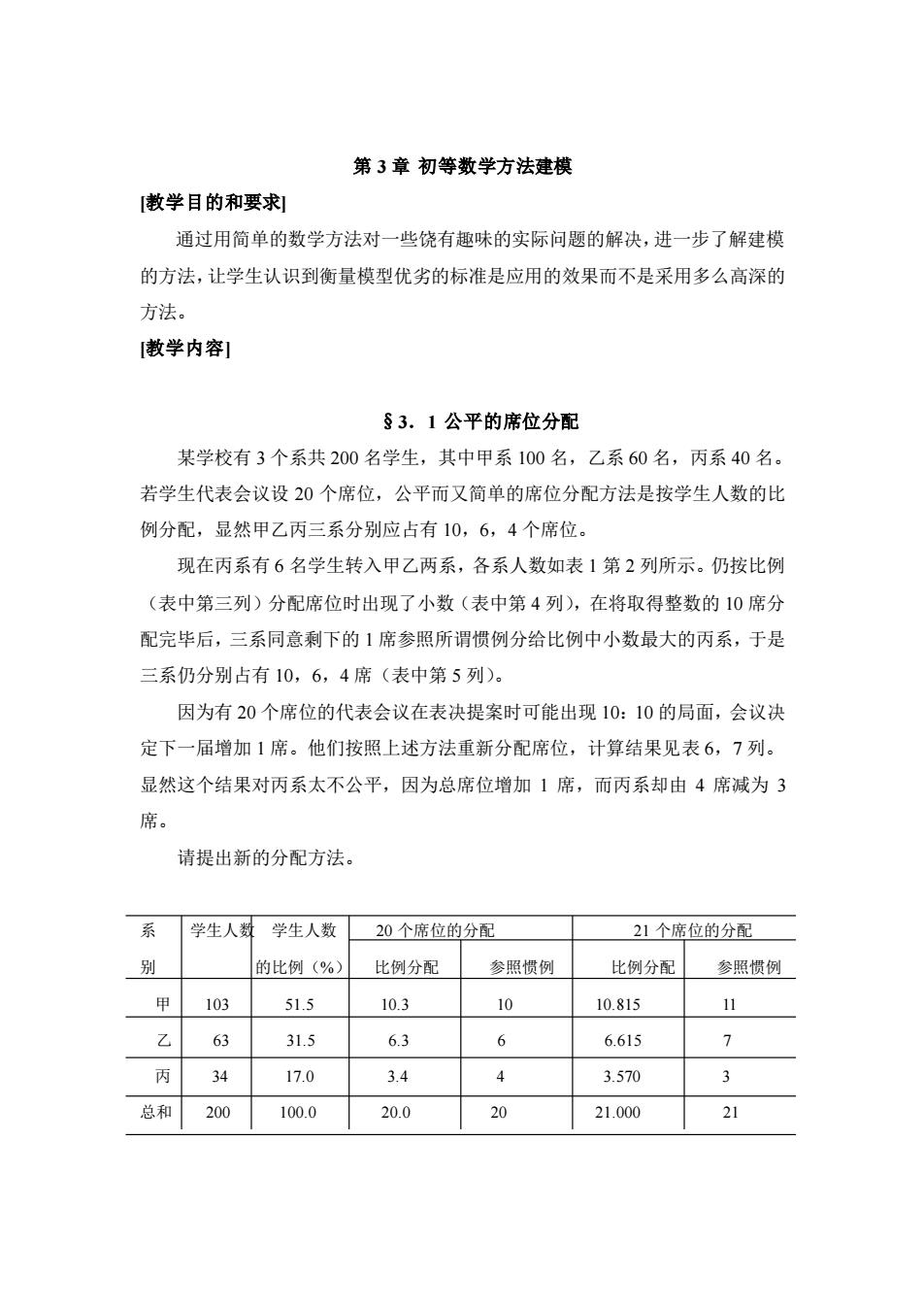
第3章初等数学方法建模 [散学目的和要求! 通过用简单的数学方法对一些饶有趣味的实际问题的解决,进一步了解建模 的方法,让学生认识到衡量模型优劣的标准是应用的效果而不是采用多么高深的 方法。 散学内容】 §3.1公平的席位分配 某学校有3个系共200名学生,其中甲系100名,乙系60名,丙系40名。 若学生代表会议设20个席位,公平而又简单的席位分配方法是按学生人数的比 例分配,显然甲乙丙三系分别应占有10,6,4个席位。 现在丙系有6名学生转入甲乙两系,各系人数如表1第2列所示。仍按比例 (表中第三列)分配席位时出现了小数(表中第4列),在将取得整数的10席分 配完毕后,三系同意剩下的1席参照所谓惯例分给比例中小数最大的丙系,于是 三系仍分别占有10,6,4席(表中第5列)。 因为有20个席位的代表会议在表决提案时可能出现10:10的局面,会议决 定下一届增加1席。他们按照上述方法重新分配席位,计算结果见表6,7列。 显然这个结果对丙系太不公平,因为总席位增加1席,而丙系却由4席减为3 席。 请提出新的分配方法。 学生人数学生人数20个席位的分配 21个席位的分配 的比例(%)比例分配 参照惯例 比例分配参照惯例 甲103 51.5 10.3 10 10.815 11 63 31.5 6.3 6 6.615 1 丙34 17.0 3.4 3.570 3 总和200 100.0 20.0 20 21000 21
第 3 章 初等数学方法建模 [教学目的和要求] 通过用简单的数学方法对一些饶有趣味的实际问题的解决,进一步了解建模 的方法,让学生认识到衡量模型优劣的标准是应用的效果而不是采用多么高深的 方法。 [教学内容] §3.1 公平的席位分配 某学校有 3 个系共 200 名学生,其中甲系 100 名,乙系 60 名,丙系 40 名。 若学生代表会议设 20 个席位,公平而又简单的席位分配方法是按学生人数的比 例分配,显然甲乙丙三系分别应占有 10,6,4 个席位。 现在丙系有 6 名学生转入甲乙两系,各系人数如表 1 第 2 列所示。仍按比例 (表中第三列)分配席位时出现了小数(表中第 4 列),在将取得整数的 10 席分 配完毕后,三系同意剩下的 1 席参照所谓惯例分给比例中小数最大的丙系,于是 三系仍分别占有 10,6,4 席(表中第 5 列)。 因为有 20 个席位的代表会议在表决提案时可能出现 10:10 的局面,会议决 定下一届增加 1 席。他们按照上述方法重新分配席位,计算结果见表 6,7 列。 显然这个结果对丙系太不公平,因为总席位增加 1 席,而丙系却由 4 席减为 3 席。 请提出新的分配方法。 系 学生人数 学生人数 20 个席位的分配 21 个席位的分配 别 的比例(%) 比例分配 参照惯例 比例分配 参照惯例 甲 103 51.5 10.3 10 10.815 11 乙 63 31.5 6.3 6 6.615 7 丙 34 17.0 3.4 4 3.570 3 总和 200 100.0 20.0 20 21.000 21

分析:从表中可见,分配的席位从20->21,丙队名额从4>3,显然是不合理的。 为了给出席位分配方案,我们先讨论A,B两方的席位分配方案。 设两方的认输为PP2,占有席位为n1,n2;如p,m,>p,m,这样不公平程度可用 P,m,P,m2来衡量:但这是一个绝对指标,有其不合理性,如P,=120,P,=100,n, =n,=10及p,=1020,P2=1000,n,=n,=10两种情况指标值是一样的 所以我们引入相对指标 r(an(P血-pm/p,/A) 为对A的不公平度。 如p,血,<p,血2,可定义对B的不公平度 r()=(pz/n2-P/)/(P/) 当总席位增加一个时,要么分给A要么分给B,不失一般性可设p,血,>P,m,即 对A不公平。当再分配一个席位时可能有以下3种可能。 1、P,(n,+1)>P,m2,说明给A增加一个仍然对A不公平,自然分给A。 2、P,m,+)<p,,说明给A增加一个席位对B不公平,计算bl+1,n2) 3、P,m,p,(n2+l),说明给B增加一个席位对A不公平,计算ranl,n2+1) 这样如果r,(,+1,n2K,(n2+1)则给A方,否则给B. 而上式又等价于 m,+)n+) 这样我们定义 C=m,(m +1) 增加的一席分配给Q值较大的一方。这种席位分配的方法称为Q值法。 §3.2划艇比赛的成绩 赛艇是一种靠桨手划桨前进的小船,分单人艇、双人艇、四人艇,八人艇四
分析:从表中可见,分配的席位从 20->21,丙队名额从 4->3,显然是不合理的。 为了给出席位分配方案,我们先讨论 A,B 两方的席位分配方案。 设两方的认输为 p ,p1 2 ,占有席位为 n ,n1 2 ; 如 p /n >p /n 1 1 2 2 这样不公平程度可用 p /n -p /n 1 1 2 2 来衡量;但这是一个绝对指标,有其不合理性,如 p1 =120, p2 =100, n1 = n2 =10 及 p1 =1020, p2 =1000, n1 =n2 =10 两种情况指标值是一样的。 所以我们引入相对指标 a 1 2 1 1 2 2 2 2 r (n ,n )=( p /n -p /n )/ (p /n ) 为对 A 的不公平度。 如 p /n <p /n 1 1 2 2 ,可定义对 B 的不公平度 b 1 2 2 2 1 1 1 1 r (n ,n )=( p /n -p /n )/ (p /n ) 当总席位增加一个时,要么分给 A 要么分给 B,不失一般性可设 p /n >p /n 1 1 2 2 ,即 对 A 不公平。当再分配一个席位时可能有以下 3 种可能。 1、p /(n +1) p /n 1 1 2 2 ,说明给 A 增加一个仍然对 A 不公平,自然分给 A。 2、p /(n +1) <p /n 1 1 2 2 , 说明给 A 增加一个席位对 B 不公平,计算 rb(n1+1,n2)。 3、p /n <p /(n +1) 1 1 2 2 ,说明给 B 增加一个席位对 A 不公平,计算 ra(n1,n2+1)。 这样如果 b 1 2 a 1 2 r (n +1,n )< r (n ,n +1) 则给 A 方,否则给 B. 而上式又等价于 2 2 2 1 2 2 1 1 ( ) ( ) 1 1 p p n n n n + + 这样我们定义 2 ( )1 i i i i p Q n n = + , 增加的一席分配给 Q 值较大的一方。这种席位分配的方法称为 Q 值法。 §3.2 划艇比赛的成绩 赛艇是一种靠桨手划桨前进的小船,分单人艇、双人艇、四人艇,八人艇四
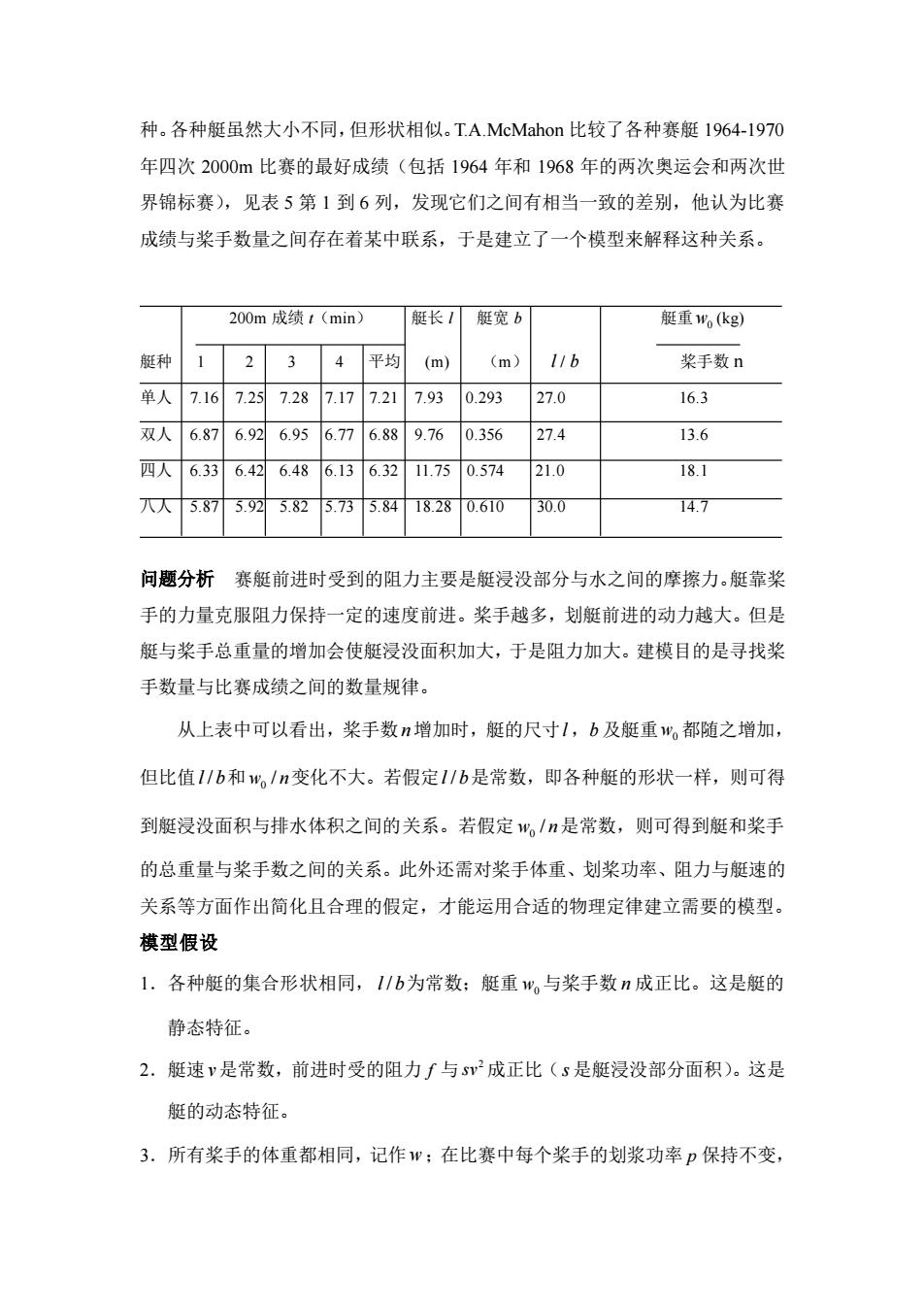
种。各种艇虽然大小不同,但形状相似。TA.McMahon比较了各种赛艇1964-1970 年四次2000m比赛的最好成绩(包括1964年和1968年的两次奥运会和两次世 界锦标赛),见表5第1到6列,发现它们之间有相当一致的差别,他认为比赛 成绩与桨手数量之间存在着某中联系,于是建立了一个模型来解释这种关系。 200m成锁1(min) 艇长1艇宽6 艇重Mkg 艇种1234平均(m) (m) 11b 奖手数n 单人7167.27287177.21793 0.29327.0 16.3 双人6876.926956.776889760.356 27.4 13.6 四人6.336.426.486.136.3211.75 0.574 21.0 18.1 八人5.8759%5825735.848280.60 30.0 147 问题分析赛艇前进时受到的阻力主要是艇浸没部分与水之间的摩擦力。艇靠桨 手的力量克服阻力保持一定的速度前进。桨手越多,划艇前进的动力越大。但是 艇与桨手总重量的增加会使艇浸没面积加大,于是阻力加大。建模目的是寻找桨 手数量与比赛成绩之间的数量规律。 从上表中可以看出,桨手数增加时,艇的尺寸1,b及艇重"。都随之增加, 但比值I/b和w。/n变化不大。若假定1/b是常数,即各种艇的形状一样,则可得 到艇浸没面积与排水体积之间的关系。若假定,/是常数,则可得到艇和桨手 的总重量与桨手数之间的关系。此外还需对桨手体重、划桨功率、阻力与艇速的 关系等方面作出简化且合理的假定,才能运用合适的物理定律建立需要的模型。 模型假设 1.各种艇的集合形状相同,I/b为常数:艇重w,与桨手数n成正比。这是艇的 静态特征。 2.艇速v是常数,前进时受的阻力∫与s成正比(s是艇浸没部分面积)。这是 艇的动态特征。 3.所有桨手的体重都相同,记作w:在比赛中每个桨手的划浆功率p保持不变
种。各种艇虽然大小不同,但形状相似。T.A.McMahon 比较了各种赛艇 1964-1970 年四次 2000m 比赛的最好成绩(包括 1964 年和 1968 年的两次奥运会和两次世 界锦标赛),见表 5 第 1 到 6 列,发现它们之间有相当一致的差别,他认为比赛 成绩与桨手数量之间存在着某中联系,于是建立了一个模型来解释这种关系。 200m 成绩 t(min) 艇长 l 艇宽 b 艇重 w0 (kg) 艇种 1 2 3 4 平均 (m) (m) l / b 桨手数 n 单人 7.16 7.25 7.28 7.17 7.21 7.93 0.293 27.0 16.3 双人 6.87 6.92 6.95 6.77 6.88 9.76 0.356 27.4 13.6 四人 6.33 6.42 6.48 6.13 6.32 11.75 0.574 21.0 18.1 八人 5.87 5.92 5.82 5.73 5.84 18.28 0.610 30.0 14.7 问题分析 赛艇前进时受到的阻力主要是艇浸没部分与水之间的摩擦力。艇靠桨 手的力量克服阻力保持一定的速度前进。桨手越多,划艇前进的动力越大。但是 艇与桨手总重量的增加会使艇浸没面积加大,于是阻力加大。建模目的是寻找桨 手数量与比赛成绩之间的数量规律。 从上表中可以看出,桨手数 n 增加时,艇的尺寸 l ,b 及艇重 w0 都随之增加, 但比值 l b/ 和 0 w n/ 变化不大。若假定 l b/ 是常数,即各种艇的形状一样,则可得 到艇浸没面积与排水体积之间的关系。若假定 0 w n/ 是常数,则可得到艇和桨手 的总重量与桨手数之间的关系。此外还需对桨手体重、划桨功率、阻力与艇速的 关系等方面作出简化且合理的假定,才能运用合适的物理定律建立需要的模型。 模型假设 1.各种艇的集合形状相同, l b/ 为常数;艇重 w0 与桨手数 n 成正比。这是艇的 静态特征。 2.艇速 v 是常数,前进时受的阻力 f 与 2 sv 成正比( s 是艇浸没部分面积)。这是 艇的动态特征。 3.所有桨手的体重都相同,记作 w ;在比赛中每个桨手的划浆功率 p 保持不变

且p与w成正比。 模型构成 有n名桨手的艇的总功率p与阻力f和速度v的乘积成正比,即 np o fy (1) 由假设2,3 fosv-.pow 代入(1)式可得 x( (2) 由假设1,各种艇几何形状相同,若艇浸没面积s与艇的某特征尺寸c的平 方成正比(sc2),则艇的排水体积A必与c的立方成正比(Ac3),于是有 (3) 又根据艇重W。与桨手数n成正比,所以艇和桨手的总重量w'=W。+mv也与 n成正比,即 w'ccn (4) 而由阿基米德定律,艇排水体积与总重量w'成正比,即 Accw' (5) 由(3),(4),(5)有 6 将(6)代入(2)式,当w是常数时得到 因为比赛成绩1(时间)与v成反比,所以就得到了 In (8 模型检验 设1与n的关系为 1=an
且 p 与 w 成正比。 模型构成 有 n 名桨手的艇的总功率 np 与阻力 f 和速度 v 的乘积成正比,即 np fv (1) 由假设 2,3 2 f sv p w , 代入(1)式可得 1 3 ( ) n v s (2) 由假设 1,各种艇几何形状相同,若艇浸没面积 s 与艇的某特征尺寸 c 的平 方成正比( 2 s c ),则艇的排水体积 A 必与 c 的立方成正比( 3 A c ),于是有 2 3 s A (3) 又根据艇重 w0 与桨手数 n 成正比,所以艇和桨手的总重量 0 w w nw ' = + 也与 n 成正比,即 w n ' (4) 而由阿基米德定律,艇排水体积与总重量 w' 成正比,即 A w ' (5) 由(3),(4),(5)有 2 3 s n (6) 将(6)代入(2)式,当 w 是常数时得到 1 9 v n (7) 因为比赛成绩 t (时间)与 v 成反比,所以就得到了 1 9 t n − (8) 模型检验 设 t 与 n 的关系为 t n =

a和B为待定系数。对上式两边取1og,得到 logt=a'+Blogn 利用最小二乘法根据所给数据拟合上式,得到 t=7.2In-om 可以看出(8)式与这个结果吻合得相当好。 §3.3录象机计数器的用途 老式的录象机上都有计数器,而没有计时器,一些录音机也有类似的情况。 这种计数器有什么用呢,让我们从这样一个问题开始:一盘表明180分钟的录象 带从头转到尾,用时184分钟,计数器从0000变到6061。在某一次使用中录象 带己经转过大半,计数器读数为4450,问剩下的一段还能否录下一小时的节目。 如果计数器读数随着录象带的转动是均匀增加的,那么由于4450已经显著 地超过6041的三分之二,即录象带已经转了两小时多,所以显然不能再录一小 时的节目。但是你细心地观察一下就会发现,读数并非均匀增长而是先快后慢, 这样,回答上面的问题就需要知道读数器读数与录象带转过的时间之间的关系。 本节目的就是建立表述这个关系的数学模型。 首先,我们要找出计数器读数(记)与录象带转过的时间(记t)之间的 关系,即建立一个数学模型t=f(m) 模型假设 1录象带的线速度是常数 2.计数器读数n与右轮盘转的圈数(m)成正比,m=kk为比例系数: 3录象带厚度是常数w,空右轮盘半径为: 4.初始时刻仁0时n=0. 模型建立 由录象带转m圈的长度和线速度的关系得 2)w 考虑到w比r小得多及m=k易得
和 为待定系数。对上式两边取 log ,得到 log ' log t n = + 利用最小二乘法根据所给数据拟合上式,得到 0.111 t n 7.21 − = 可以看出(8)式与这个结果吻合得相当好。 §3.3 录象机计数器的用途 老式的录象机上都有计数器,而没有计时器,一些录音机也有类似的情况。 这种计数器有什么用呢,让我们从这样一个问题开始:一盘表明 180 分钟的录象 带从头转到尾,用时 184 分钟,计数器从 0000 变到 6061。在某一次使用中录象 带已经转过大半,计数器读数为 4450,问剩下的一段还能否录下一小时的节目。 如果计数器读数随着录象带的转动是均匀增加的,那么由于 4450 已经显著 地超过 6041 的三分之二,即录象带已经转了两小时多,所以显然不能再录一小 时的节目。但是你细心地观察一下就会发现,读数并非均匀增长而是先快后慢, 这样,回答上面的问题就需要知道读数器读数与录象带转过的时间之间的关系。 本节目的就是建立表述这个关系的数学模型。 首先,我们要找出计数器读数(记 n)与录象带转过的时间(记 t)之间的 关系,即建立一个数学模型 t f n = ( ). 模型假设 1.录象带的线速度是常数 v; 2.计数器读数 n 与右轮盘转的圈数(m)成正比,m=kn,k 为比例系数; 3.录象带厚度是常数 w,空右轮盘半径为 r; 4.初始时刻 t=0 时 n=0. 模型建立 由录象带转 m 圈的长度和线速度的关系得 1 2 ( ) m i r wi vt = + = 考虑到 w 比 r 小得多及 m=kn 易得