
非线性物理:扩散限制系统的形态发生问题 生长机理:二元稀溶液 1.我们针对二元体系定向凝固问题进行机理的讨论,其它系统可以 仿照进行。第一个假定是系统液相是无穷延伸的,凝固界面前沿 温度分布满足线性关系,同时系统在动力学上是非平衡的,但是 热力学上是平衡的,即所谓准静态近似。 2.在定向凝固系统中,我们总是将分析坐标系绑定在界面处,即假 定坐标系随界面一起移动。因此有如下温度场:T)=T,+Gz,其 中T,为最初体系组元成分为c时的平衡熔点。 3.因为是定向凝固,我们来看看界面前沿浓度场的分布。扩散限制 体系的浓度场满足Laplace方程: de-voc=DV'e=D 其中V为界面生长速率,D 为组分扩散系数,c为组分 8t 浓度
非线性物理:扩散限制系统的形态发生问题 扩散限制系统的形态发生问题 生长机理:二元稀溶液 1. 我们针对二元体系定向凝固问题进行机理的讨论,其它系统可以 仿照进行。第一个假定是系统液相是无穷延伸的,凝固界面前沿 温度分布满足线性关系,同时系统在动力学上是非平衡的,但是 热力学上是平衡的,即所谓准静态近似。 2. 在定向凝固系统中,我们总是将分析坐标系绑定在界面处,即假 定坐标系随界面一起移动。因此有如下温度场:T(z)=T0+Gz,其 中T0为最初体系组元成分为c时的平衡熔点。 3. 因为是定向凝固,我们来看看界面前沿浓度场的分布。扩散限制 体系的浓度场满足Laplace方程: 其中V为界面生长速率,D 为组分扩散系数,c为组分 浓度
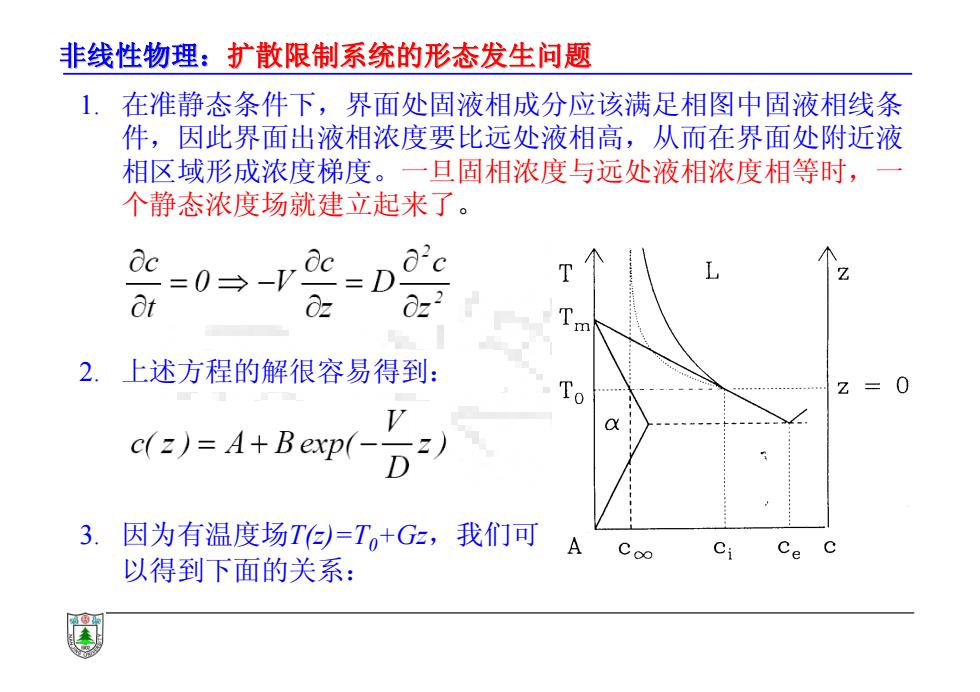
非线性物理:扩散限制系统的形态发生问题 1. 在准静态条件下,界面处固液相成分应该满足相图中固液相线条 件,因此界面出液相浓度要比远处液相高,从而在界面处附近液 相区域形成浓度梯度。一旦固相浓度与远处液相浓度相等时,一 个静态浓度场就建立起来了。 dc =0-y 0c=D9 8t T m 2.上述方程的解很容易得到 To Z=0 a c(z)=A+Bexp(- 3.因为有温度场T=T,+Gz,我们可 ACo∞ Ci Ce c 以得到下面的关系:
非线性物理:扩散限制系统的形态发生问题 扩散限制系统的形态发生问题 1. 在准静态条件下,界面处固液相成分应该满足相图中固液相线条 件,因此界面出液相浓度要比远处液相高,从而在界面处附近液 相区域形成浓度梯度。一旦固相浓度与远处液相浓度相等时,一 个静态浓度场就建立起来了。 2. 上述方程的解很容易得到: 3. 因为有温度场T(z)=T0+Gz,我们可 以得到下面的关系: