
总复习三个弹性常数O1[a°1、容许应力EGn2(1+μ)2、极限应力 x-(O,,002,0,)0E-83、安全系数:nTG-2福aG泊松比 (或横向变形系数)
n s j x 1、容许应力: s = , , } 0.2 2 : { s j x s s s s b 、极限应力 = 3、安全系数:n 泊松比(或横向变形系数) e e n = 三个弹性常数 t G= e s E= 2(1+) = E G

总复习剪切与挤压的实用计算T(合力(合力)矩形截面杆约束扭转TmaxM.max其中W_-βb3LmaxWpM.MT1其中 I,=α b40t I-Vt maxGIp注意:h≥b
n n (合力) (合力) P P Pc n n Q h b h t 1 Mn t max 注意: b 剪切与挤压的实用计算 t= t A Q c c c c A P s = s 矩形截面杆约束扭转 max 3 max : b p W W M P n t = 其中 = 4 , : I b GI M P P n q= 其中 = 1 nt max t =

总复习圆柱形密圈螺旋弹簧的计算8DPd近似值:Tmax+1rd'32D64PR'nPAGd4K精确值:m=8DPCGd4其中:其中:K=rd364R'n4C-1 0.6155.C-D为弹簧常数kC4C-4d非对称截面梁发生平面弯曲的条件①外力必须作用在主惯性面内:②中性轴为形心主轴③若是横向力,还必须过弯曲中心y
64 : 64 3 4 4 3 R n Gd K K P Gd PR n = = = 其中 圆柱形密圈螺旋弹簧的计算 为弹簧常数 精确值: 其中: ; 0.615 4 4 4 1 ; 8 max 3 d D C C C C k d DP k + = − − = = t 非对称截面梁发生平面弯曲的条件 ①外力必须作用在主惯性面内; ②中性轴为形心主轴; ③若是横向力,还必须过弯曲中心。 P x y z O max 3 8 1) 2 ( d DP D d 近似值:t = +

总复习积分法求挠曲线方程(弹性曲线)1.微分方程的积分EIf"(x)--M(x)Eif'(x)-[(-M(x)dx+CEIf(x)-J(J(-M(x)dx)dx+Cx+C
积分法求挠曲线方程(弹性曲线) EIf (x)=−M (x) d 1 EIf (x)= (−M (x)) x+C d 1 2 EIf (x)= ( (−M (x))dx) x+C x+C 1.微分方程的积分
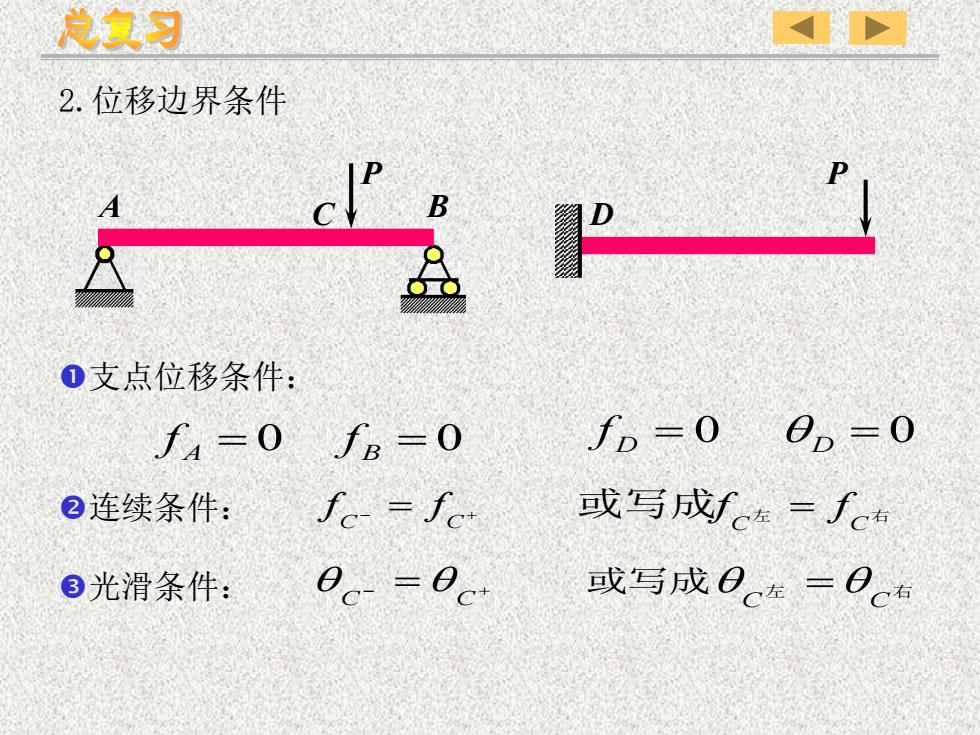
总复习2.位移边界条件DL0支点位移条件:fb=0 0,=0-f=0 f=0或写成fc左 一f右f - fc②连续条件:0。- - 0ct或写成左 =石③光滑条件:
2.位移边界条件 P A C B P D 支点位移条件: 连续条件: 光滑条件: f A = 0 f B = 0 f D = 0 q D = 0 − = + C C f f − = + C C q q 或写成 左 右 C C q =q 或写成 左 右 C C f = f