《机械工程控制基础》课程授课教案（讲义）第四章 控制系统的频率特性

§4.2 频率特性的图示方法之一 极坐标图 频率分析法的基础是画出线性系统频率特性的图形。 表现方式有多种：「实频特性与虚频特性 幅频特性与相频特性 相应的图形表示也有不同的方法，常用的〔极坐标图 (对数坐标图 极坐标图是反映频率响应的几何表示。当给定频率为。时，其G(加) 在复平面上表示一个向量OA,向量OA的端点坐标就是G(Uo)的实部和虚 部。当o:0→+0时，G(jo)是o的复变函数，是一种变换。G(jo)作为一 个失量，其端点在复平面相对应的轨迹 +极坐标图。(Nyqwist曲线) 01 ZGCh)Re 图4.3 图4.4 规定：从正实轴开始逆时针旋转为正。 一、典型环节的Nyqwist图

§4.2 频率特性的图示方法之一 极坐标图 频率分析法的基础是画出线性系统频率特性的图形。 表现方式有多种： 实频特性与虚频特性 幅频特性与相频特性 相应的图形表示也有不同的方法，常用的 极坐标图 对数坐标图 极坐标图是反映频率响应的几何表示。当给定频率为  时， 其 G j   在复平面上表示一个向量 OA ，向量 OA 的端点坐标就是 G j   的实部和虚 部。当 :0   时， G j   是  的复变函数，是一种变换。 G j   作为一 个矢量，其端点在复平面相对应的轨迹 极坐标图。(Nyqwist 曲线) 0 jw w1 w2 w3 S σ 0 Im w1 w2 w3 [G(jw)] Re w ∞ G(jw1) 图 4.3 图 4.4 规定：从正实轴开始逆时针旋转为正。 一、典型环节的 Nyqwist 图

1.比例环节：G(S)=K G(Jw)-kfG(Jo)=K C∠G(jo=0° Im [G(w)] 0 (k0 k Re 图4.5 2积分环节：GS)-号 GUo)=1了G(Uo=1 jo1∠G(Uo)=-90 -片al0 o=0,lG(Uo=∞ 位于虚轴下半轴。由无穷远→原点 具有恒定的相位滞后。 Im [G(iw)] 0w。00 4900 Re w◆0 图4.6

1.比例环节： G S K    G j K        0 0 G j K G j      Im k [G(jw)] Re (k,j0) 0 图 4.5 2.积分环节：   1 G S S    1 G j j        0 1 90 G j G j        1 j       0, , 0 G j G j           位于虚轴下半轴。由无穷远 原点。 具有恒定的相位滞后。 0 Im w [G(jw)] Re w ∞ -900 0 图 4.6

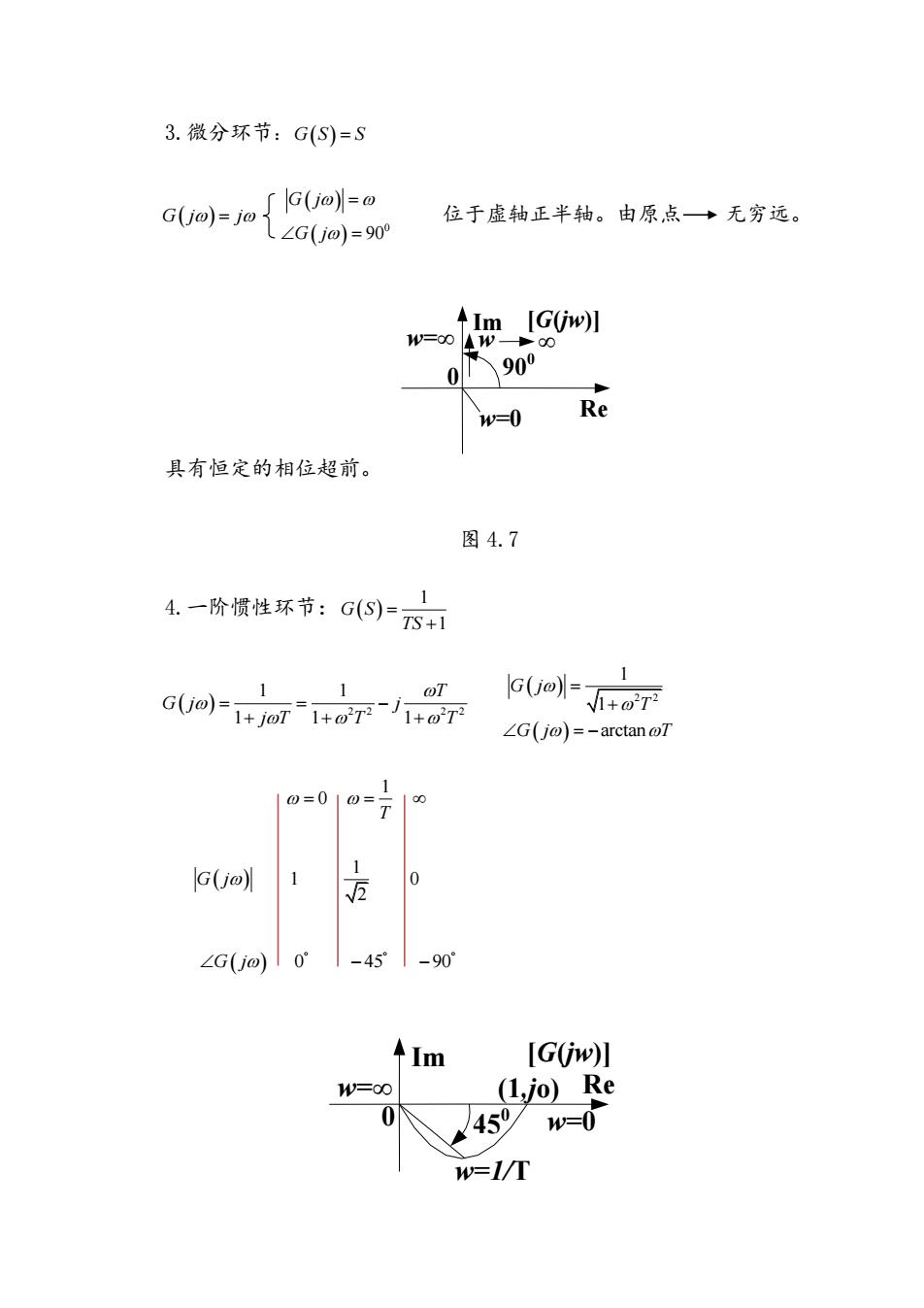
3.微分环节：G(S)=S GUo)-G(o)- 位于虚轴正半轴。由原点→无穷远。 L∠G(jo)=90° ImIG0w川 W=00W 090 w=0 Re 具有恒定的相位超前。 图4.7 4.一阶惯性环节：G(S)=S+ G(Jo)-1+JoT GUO)-+T ∠G(jo)=-arctanoT 10=010=7 G(jo 1 0 ∠G(j@)0 -451-90 41m G(iw) W=00 (1,jo)Re 0 459w=0 w=/T

3.微分环节： G S S    G j j          0 90 G j G j       位于虚轴正半轴。由原点 无穷远。 具有恒定的相位超前。 0 Im w=0 [G(jw)] Re w ∞ 900 w=∞ 图 4.7 4.一阶惯性环节：   1 1 G S TS     2 2 2 2 1 1 1 1 1 T G j j j T T T                2 2 1 1 arctan G j T G j T          1 0 T      G j   1 1 0 2 G j   0 45 90      0 Im w=0 [G(jw)] Re 450 w=∞ (1,jo) w=1/T

图4.8 以G,)为圆心，以)为半径的一个正实轴下的半圆。可见个， G(jo↓，低通滤波的性能存在相位滞后，o个，p(@)↑，最大相位滞后90°。 5.一阶微分环节（导前环节）G(S)=S+1 o=0=7o→m GUo)=1+jorG(Uo=i+示 45 190 L∠G(jo)=arctan @T [G(w)] 1AW。00 450/=1T 0 (1jo)Re 0 图4.9 始于点（山，），平行于虚轴，在第一象限的一条垂线。 6.二阶振荡环节G(S)S+250.S+a 02 (0<5<) 0,2（-o2+o,2-j2500) 频率特性：GU)-+o+250o(包，2-0+45oo 令= 0n4-02o2 25o0 8-+2aa-+45a河/a-a于+ga河

图 4.8 以 0 1 ( ) 2 ，j 为圆心，以 1 2 为半径的一个正实轴下的半圆。可见  ， G j    ，低通滤波的性能存在相位滞后，  ，    ，最大相位滞后 90。 5.一阶微分环节(导前环节) G S TS    1 G j j T      1     2 2 1 arctan G j T G j T         1 0 1 2 0 45 90 T            0 Im w=0 [G(jw)] Re w ∞ 450 w=∞ (1,jo) w=1/T 图 4.9 始于点 1, j 0  ，平行于虚轴，在第一象限的一条垂线。 6.二阶振荡环节     2 2 2 0 1 2 n n n G S S S          频率特性：       2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 n n n n n n n n j G j j                           令 n       2 1 1 2   j        4 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 4 4 n n n n n n n j                      

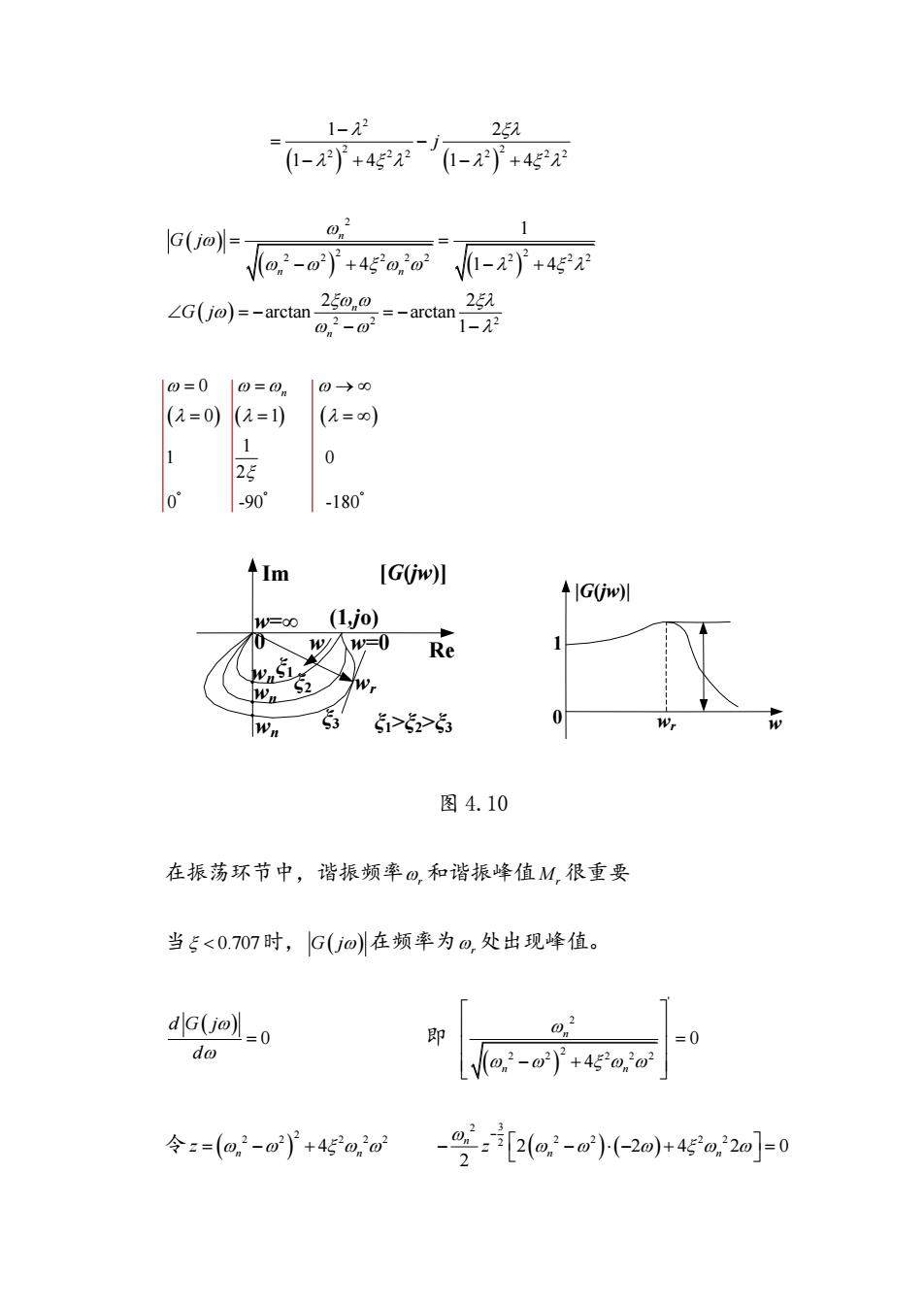
1-2 25 -y+45-+458 1 G(j@)=- a-》+4gao-xy+458 c(o-c2台-amm2务 02-07 0=0|0=0n|0→0 (2=0)(2=1)(2=∞) 1 0 25 10 -90° -180 im [G(w)l ↑IG0w =00 (1jo) 义0Re 52 5>5>5 图4.10 在振荡环节中，谐振频率@，和谐振峰值M,很重要 当5<0.707时，G(Uo在频率为@，处出现峰值。 dG(j)=0 0,2 do [Vo:-0)+ 令：=(o,2-m+45a,o2 -受：[2o-a-2oj+45a2a]-0

    2 2 2 2 2 2 2 2 2 1 2 1 4 1 4 j                        2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 4 1 4 2 2 arctan arctan 1 n n n n n G j G j                                     0 0 1 1 1 0 2 0 -90 -180     n                0 Im w=0 [G(jw)] Re ξ3 w=∞ (1,jo) wr wn wn wn ξ2 ξ1 ξ1>ξ2>ξ3 w 0 |G(jw)| 1 wr w 图 4.10 在振荡环节中，谐振频率 r 和谐振峰值 M r 很重要 当   0.707 时， G j   在频率为 r 处出现峰值。   0 d G j d    即   ' 2 2 2 2 2 2 2 0 4 n n n                    令   2 2 2 2 2 2 4 n n z             2 3 2 2 2 2 2 2 2 4 2 0 2 n n n z                  