山东理工大学：《电路》课程教学资源（课件讲稿）第7章 一阶电路和二阶电路的时域分析

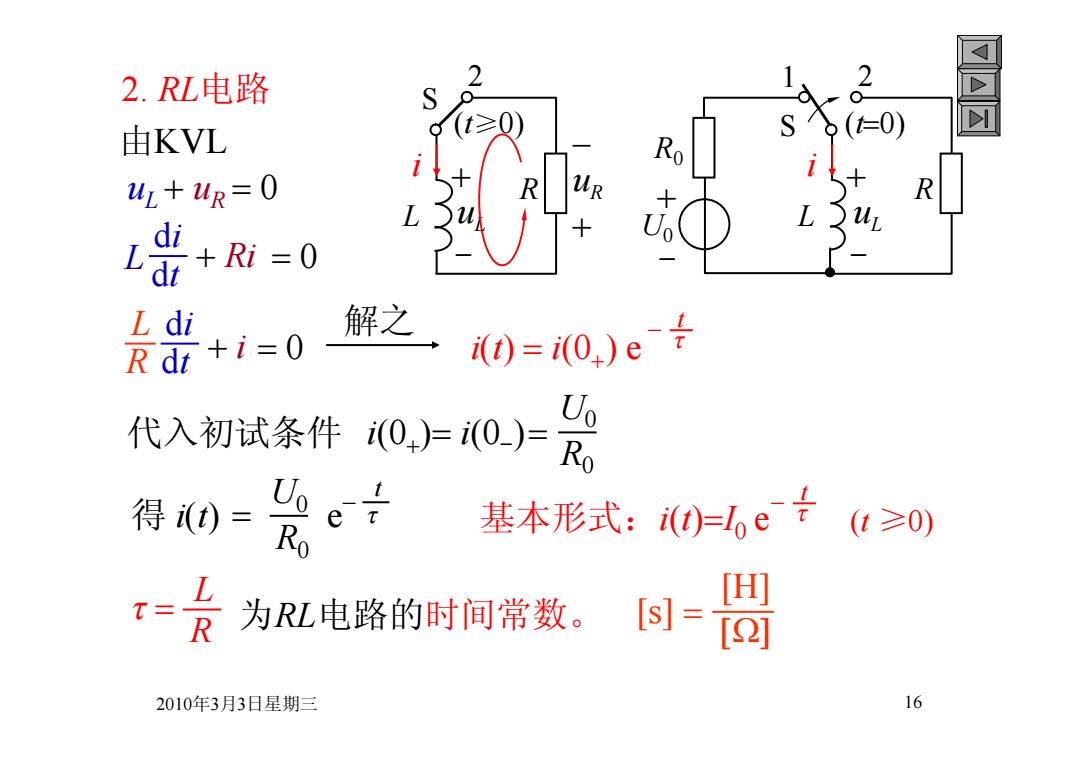
2.RL电路 2 EN =0) 由KVL R uL+uR=O di L +Ri=0 L di Rdi +i=0 解之 0=i0)e 代入初试条件(0+)=(0)= U Ro 得)= e Ro 基本形式：0=1e÷( ≥0) T= R 为L电路的时间常数。 [s]= 2] 2010年3月3日星期三 16

2010年3月3日星期三 16 2. RL电路 由KVL uLuR 0 S  R  (t0) R0 L 1 2 uL   i U0 R (t≥0) L uL   i S 2   uR di L dt Ri 0 di dt L i 0 R i(0)i(0- ) R0 U0 i(t) i(0) e  R0 U0  R L 为RL电路的时间常数。  t e [s]  [H]  t 得 i(t) 解之 代入初试条件 基本形式：i(t)I0 e  t (t ≥0)

i0)=1oe￥ i,Uk,UL E 0) RIo 电阻和电感上的 电压分别为： WR t uR Ri =Rle÷,u≥0y uL 4,=-R=-R16e÷,e≥0) 或者：4=L-R,e÷,≥0 2010年3月3日星期三 17

2010年3月3日星期三 17 电阻和电感上的 电压分别为： R (t≥0) L uL   i S 2   uR RI0 uR t o i, uR , uL i I 0 uL RI0 uR Ri R I0 e uLuR R I0 e di dt 或者：uL L R I0 e i(t) I0 e  t  t  t  t ，(t ≥0) ，(t ≥0) ，(t ≥0)

3.例题分析P144例7-2 0.1892 t≥0 试求：x;(0)和(0)： R i(t)和uy();uv(0)。解： U uy Ry 35V 5k L 0.398 T-R+Rv 0.398H 0.189+5×103 某300kW汽轮发电机 =79.6(（us) 励磁回路的电路模型 0)≈R =35 0.189 =185.2A=i(0) 实践中，要 i(t)=185.2e-12560tA 切断L的电 流，必须考 u()=-Ryi(t)）=-926e-12560tkV 虑磁场能量 u,(0)=926kV!电压表的量程才50V。的释放问题 2010年3月3日星期三 18

2010年3月3日星期三 18 3.例题分析 P144 例7-2 试求：；i(0)和i(0) ； i(t)和uV (t) ；uV (0)。 V  S  R L   U RV uV i 0.189 0.398H 5k 35V 某300kW汽轮发电机 励磁回路的电路模型 电压表的量程才50V。  R+RV L  0.1895×103 0.398 s) i(0)≈ R U  0.189 35 185.2 A i(t) 185.2 e -12560t A uV (tRV i(t926 e -12560t kV uV (0) 926 kV ! t≥0+ 实践中，要 切断 L 的电 流，必须考 虑磁场能量 的释放问题 解： i(0)

§7-3一阶电路的零状态响应 AE >零状态响应：在动态元件 S(t R 初值为0的状态下，外施 激励引起的响应。 1.RC电路 由KVL:r+uc=Us 对应的齐次方程： duc ug=Ri=RC dr RC- +uc=0 dt s+uc=Us RC dt 通解：u”c=Ae 常系数非齐次线性方程 特解：Wc=Us 其解为：uc=l'c+u'c 所以：4c=+Ae 2010年3月3日星期三 19

2010年3月3日星期三 19 §7-3 一阶电路的零状态响应 零状态响应：在动态元件 初值为 0 的状态下，外施 激励引起的响应。 1. RC电路 由KVL： uR uCUS S US   (t=0)   uC R C  uR  i uRRi duc dt RC duc dt RC uC US 常系数非齐次线性方程 对应的齐次方程： 其解为：uC u'Cu"C 通解： u"CA e 1 RC  t 特解： u'C US 所以： uC US A e duc dt RC uC0 1 RC  t

s+uc=Us RC dt uc=Us+Ae Rc Us 代入初值：uc(0+)=uc(0)=0 求得：A=-Us uc,i稳态分量 所以零状态响应为 Us --- t uc=Us(1-e )7=RC R uc=u6+u吧 i= d业- se号 瞬态分量 4=-U,e 2010年3月3日星期三 20

2010年3月3日星期三 20 代入初值：uC (0) uC (0) 0 求得：AUS 所以零状态响应为 uCUS (1e  )，  t uC '' 稳态分量 uC ' 瞬态分量 duc dt i C  R US e  t i S US   (t≥0)   uC R C  uR  i duc dt RC uCUS uC US A e 1 RC  t RC uCuCuC US t o uC , i R US US ' '' uCUSUS e  t