
(2)高度分散系统的单位表面吉布斯函数 OAs ).p.(B) 单位表面吉布斯函数σ的物理意义 是在定温、定压和定组成的情况下,系 统吉布斯函数随表面积的变化率。 dG.()=o dAs
(2) 高度分散系统的单位表面吉布斯函数 S T , p,n( ) B A G ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ σ = 单位表面吉布斯函数σ 的物理意义 是在定温、定压和定组成的情况下,系 统吉布斯函数随表面积的变化率。 dGT,p,n(B) = σ dAS

例10-125℃时,把半径为1.00×10-3m 的水滴分散成半径为1.00×10-6m的小水滴 (1)其体积表面增加了多少倍? (2)单位表面吉布斯函数增加了多少? (3)完成该变化时,环境至少要做多少功 ?已知该温度时,水的表面张力为0.07275 Nm-l。 解:己知:r1=1.00×10-3m r2=1.00×10-6m σ=0.07275Nm-1
例 10-1 25℃时,把半径为1.00×10-3m 的水滴分散成半径为1.00×10-6m的小水滴 。(1)其体积表面增加了多少倍? (2)单位表面吉布斯函数增加了多少? (3)完成该变化时,环境至少要做多少功 ?已知该温度时,水的表面张力为0.07275 N·m-1。 解:已知:r1=1.00×10-3m r2=1.00×10-6m σ=0.07275N·m-1

4πr2 3 (1)Av= As V 4 3 A2= 1.00×10-3 2=1000 AvA 31.00×10-6 体积表面增加了1000倍
(1) r r r V A AV 3 3 4 4 3 2 S = = = π π 1000 1.00 10 1.00 10 6 3 2 1 ,1 ,2 = × × = = − − m m r r A A V V 体积表面增加了1 000倍
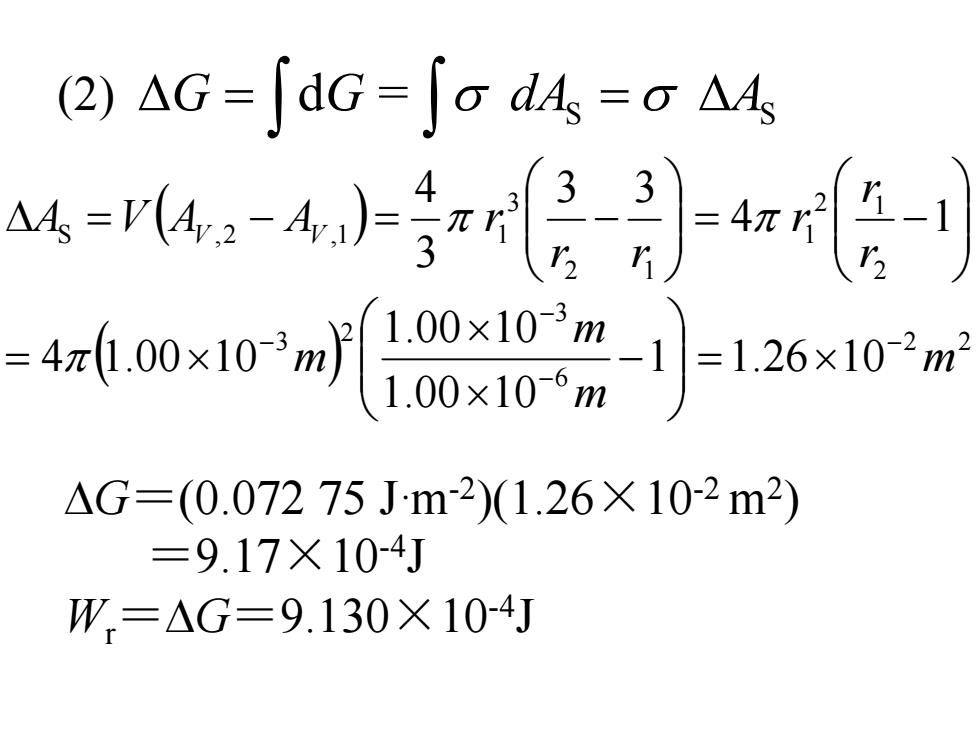
(2)AG=∫dG=∫adA=o△4 姓:小2》语 =twnl88g-1s10 △G=(0.07275Jm2)(1.26×10-2m2) =9.17×104灯 W,=△G=9.130×104灯
(2) = S S ∆G = dG dA = ∆A ∫ ∫σ σ ( ) ⎟⎟⎠⎞ ⎜⎜⎝⎛ = − ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∆ = − = − 4 1 3 3 34 2 2 1 1 2 1 3 S ,2 ,1 1 rr r r r A V A A r V V π π ( ) 2 2 63 2 3 1 1.26 10 1.00 10 1.00 10 4 1.00 10 m mm m − −− − = × ⎟⎟⎠⎞ ⎜⎜⎝⎛ − ×× = π × ∆G=(0.072 75 J·m-2)(1.26×10-2 m2) =9.17×10-4J Wr=∆G=9.130×10-4J

4、影响表面张力的因素 ()表面张力与物质本性的关系 o(金属键)>o(离子键)>o(极 性共价键)>σ(非极性共价键)
4、 影响表面张力的因素 (1) 表面张力与物质本性的关系 σ(金属键)>σ(离子键)>σ(极 性共价键)>σ(非极性共价键)