自动控制原理实验指导书 则反馈系统的传递函数: >G1=tf1,[1,2,1])y G2=tf1,[1,1])月 G=feedback(G1,G2) 运行结果: Transfer function: s+1 sM3+3s^2+3s+2 若采用正反馈连接结构输入命令 >>G=feedback(G1,G2,1) 则得出如下结果: Transfer function: s+1 s^3+3s2+3s 例7若反馈系统为更复杂的结构如图2-1所示。其中 s3+7s2+24s+24 G(S)= s4+10s3+35s2+50s+24 ,G(s)=0,Hs)=0.0s+ R(s) C(s) G(5) G(s) (s) 图2-1复杂反馈系统 则闭环系统的传递函数: >G1=tf[1,7,24,2411,10,35,50,24] G2=tf[10,5],[1,0]): H=tf[1],[0.01,1) G a=feedback(G1*G2,H) 结果为: Transfer function: 10
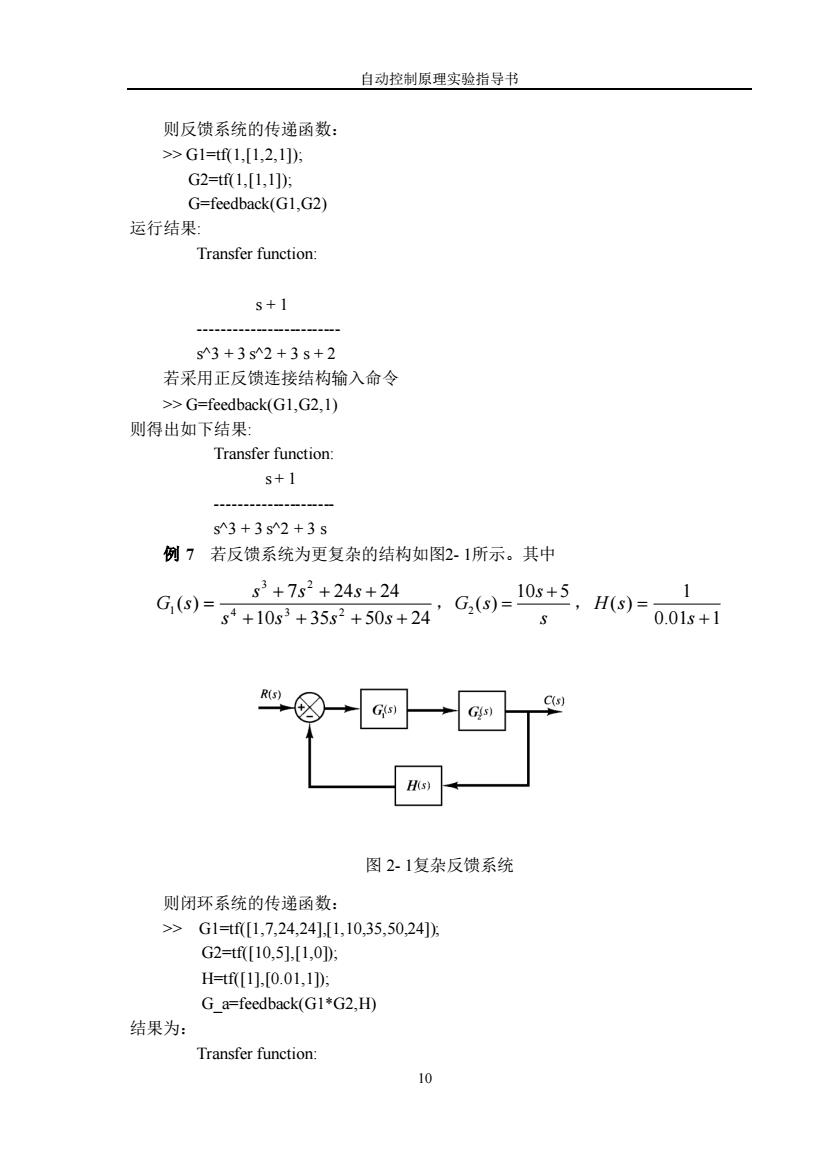
自动控制原理实验指导书 10 则反馈系统的传递函数: >> G1=tf(1,[1,2,1]); G2=tf(1,[1,1]); G=feedback(G1,G2) 运行结果: Transfer function: s + 1 ------------------------- s^3 + 3 s^2 + 3 s + 2 若采用正反馈连接结构输入命令 >> G=feedback(G1,G2,1) 则得出如下结果: Transfer function: s + 1 --------------------- s^3 + 3 s^2 + 3 s 例 7 若反馈系统为更复杂的结构如图2- 1所示。其中 10 35 50 24 7 24 24 ( ) 4 3 2 3 2 1 + + + + + + + = s s s s s s s G s , 2 10 5 ( ) s G s s + = , 0.01 1 1 ( ) + = s H s 图 2- 1复杂反馈系统 则闭环系统的传递函数: >> G1=tf([1,7,24,24],[1,10,35,50,24]); G2=tf([10,5],[1,0]); H=tf([1],[0.01,1]); G_a=feedback(G1*G2,H) 结果为: Transfer function:

自动控制原理实验指导书 0.1s^5+10.75s^4+77.75s3+278.6s^2+361.2s+120 0.01s^6+1.1s^5+20.35s^4+110.5s^3+325.2s^2+384s+120 2s+1 【自我实践5】已知系统前向通道的传递函数G(S)= 32+25+3 求其单位负反馈 闭环传递函数。 5、Simulink建模方法 在一些实际应用中,如果系统的结构过于复杂,不适合用前面介绍的方法建模。 在这种情况下,功能完善的Simulink程序可以用来建立新的数学模型。Simulink是由 Math Works软件公司1990年为MATLAB提供的新的控制系统模型图形输入仿真工 具。它具有两个显著的功能:Simul(仿真)与Link(连接),即可以利用鼠标在模型窗口 上“画”出所需的控制系统模型。然后利用SIMULINK提供的功能来对系统进行仿真或 线性化分析。与MATLAB中逐行输入命令相比,输入更容易,分析更直观。下面简 单介绍SIMULINK建立系统模型的基本步骤: (1) SIMULINK的启动:在MATLAB命令窗口的工具栏中单击按钮等或者在 命令提示符>>下键入simulink命令,回车后即可启动Simulink程序。启动后软件自动 打开Simullink模型库窗口,如 图2-3所示。这一模型库中含有许多 子模型库,如Sources((输入源模块库)、Sinks(输出显示模块库)、Nonlinear(非线性环节) 等。若想建立一个控制系统结构框图,则应该选择File New菜单中的Model选项, 或选择工具栏上new Model凸按钮,打开一个空白的模型编辑窗口如错误:未找到引 用源。所示。 回为因n1M 回☒ Eile Edit yie Siwalatioa Fgemst Ieola Belp D含#刷 Cantinons:staulirk/Contixou Sienlink Cootinarus 匀gt Junetioas a Talles Discrvie Sonlinaur Puctioas Tables -习35nis4Smt Sowrces 匀5动tm Coutral Srrten Ttolhex 春步 图2-2 simulink模型库 图2-3模型编辑窗口 (2) 画出系统的各个模块:打开相应的子模块库,选择所需要的元素,用鼠标左 键点中后拖到模型编辑窗口的合适位置。 (3) 给出各个模块参数:由于选中的各个模块只包含默认的模型参数,如默认的 传递函数模型为1/(s+1)的简单格式,必须通过修改得到实际的模块参数。要修改模块 11
自动控制原理实验指导书 11 0.1 s^5 + 10.75 s^4 + 77.75 s^3 + 278.6 s^2 + 361.2 s + 120 -------------------------------------------------------------------- 0.01 s^6 + 1.1 s^5 + 20.35 s^4 + 110.5 s^3 + 325.2 s^2 + 384 s + 120 【自我实践 5】已知系统前向通道的传递函数 2 2 1 ( ) 2 3 s G s s s + = + + ,求其单位负反馈 闭环传递函数。 5、Simulink 建模方法 在一些实际应用中,如果系统的结构过于复杂,不适合用前面介绍的方法建模。 在这种情况下,功能完善的 Simulink 程序可以用来建立新的数学模型。Simulink 是由 Math Works 软件公司 1990 年为 MATLAB 提供的新的控制系统模型图形输入仿真工 具。它具有两个显著的功能:Simul(仿真)与 Link(连接),即可以利用鼠标在模型窗口 上“画”出所需的控制系统模型。然后利用 SIMULINK 提供的功能来对系统进行仿真或 线性化分析。与 MATLAB 中逐行输入命令相比,输入更容易,分析更直观。下面简 单介绍 SIMULINK 建立系统模型的基本步骤: (1) SIMULINK 的启动:在 MATLAB 命令窗口的工具栏中单击按钮 或者在 命令提示符>>下键入 simulink 命令,回车后即可启动 Simulink 程序。启动后软件自动 打开 Simullink 模型库窗口,如 图2- 3所示。这一模型库中含有许多 子模型库,如 Sources(输入源模块库)、Sinks(输出显示模块库)、Nonlinear(非线性环节) 等。若想建立一个控制系统结构框图,则应该选择 File| New 菜单中的 Model 选项, 或选择工具栏上 new Model 按钮,打开一个空白的模型编辑窗口如错误!未找到引 用源。所示。 图 2- 2 simulink 模型库 图 2- 3模型编辑窗口 (2) 画出系统的各个模块:打开相应的子模块库,选择所需要的元素,用鼠标左 键点中后拖到模型编辑窗口的合适位置。 (3) 给出各个模块参数:由于选中的各个模块只包含默认的模型参数,如默认的 传递函数模型为 1/(s+1)的简单格式,必须通过修改得到实际的模块参数。要修改模块

自动控制原理实验指导书 的参数,可以用鼠标双击该模块图标,则会出现一个相应对话框,提示用户修改模块 参数。 (4) 画出连接线:当所有的模块都画出来之后,可以再画出模块间所需要的连线, 构成完整的系统。模块间连线的画法很简单,只需要用鼠标点按起始模块的输出端(三 角符号),再拖动鼠标,到终止模块的输入端释放鼠标键,系统会自动地在两个模块 间画出带箭头的连线。若需要从连线中引出节点,可在鼠标点击起始节点时按住Ctl 键,再将鼠标拖动到目的模块。 (5)指定输入和输出端子:在Simulink下允许有两类输入输出信号,第一类是仿 真信号,可从source(输入源模块库)图标中取出相应的输入信号端子,从Sink(输出显 示模块库)图标中取出相应输出端子即可。第二类是要提取系统线性模型,则需打开 Connection(连接模块库)图标,从中选取相应的输入输出端子。 例8典型二阶系统的结构图如图2-4所示。用SIMULINK对系统进行仿真分析。 R(s) E(s) 900 C(s) 5+9 图2-4典型二阶系统结构图 按前面步骤,启动simulink并打开一个空白的模型编辑窗口。 (1)画出所需模块,并给出正确的参数: ●在sources子模块库中选中阶跃输入(step)图标,将其拖入编辑窗口,并用 鼠标左键双击该图标,打开参数设定的对话框,将参数step time(阶跃时刻) 设为0。 ● 在Math(数学)子模块库中选中加法器(sum)图标,拖到编辑窗口中,并双 击该图标将参数List of signs(符号列表)设为+-(表示输入为正,反馈为负)。 ● 在continuous(连续)子模块库中、选积分器(Integrator)和传递函数(Transfer Fcn)图标拖到编辑窗口中,并将传递函数分子(Numerator)改为〔900), 分母(Denominator)改为(1,9)。 ● 在sinks(输出)子模块库中选择scope(示波器)和Outl(输出端口模块)图标并将 之拖到编辑窗口中。 (3)将画出的所有模块按错误!未找到引用源。用鼠标连接起来,构成一个原系统的 框图描述如图2-5所示。 (4)选择仿真算法和仿真控制参数,启动仿真过程。 。在编辑窗口中点击SimulationSimulation parameters菜单,出现参数对话框,在 solver模板中设置响应的仿真范围StartTime(开始时间)和StopTime(终止时间),仿 12
自动控制原理实验指导书 12 的参数,可以用鼠标双击该模块图标,则会出现一个相应对话框,提示用户修改模块 参数。 (4) 画出连接线:当所有的模块都画出来之后,可以再画出模块间所需要的连线, 构成完整的系统。模块间连线的画法很简单,只需要用鼠标点按起始模块的输出端(三 角符号),再拖动鼠标,到终止模块的输入端释放鼠标键,系统会自动地在两个模块 间画出带箭头的连线。若需要从连线中引出节点,可在鼠标点击起始节点时按住 Ctrl 键,再将鼠标拖动到目的模块。 (5) 指定输入和输出端子:在 Simulink 下允许有两类输入输出信号,第一类是仿 真信号,可从 source(输入源模块库)图标中取出相应的输入信号端子,从 Sink(输出显 示模块库)图标中取出相应输出端子即可。第二类是要提取系统线性模型,则需打开 Connection(连接模块库)图标,从中选取相应的输入输出端子。 例8 典型二阶系统的结构图如图2- 4所示。用 SIMULINK 对系统进行仿真分析。 图 2- 4 典型二阶系统结构图 按前面步骤,启动 simulink 并打开一个空白的模型编辑窗口。 (1) 画出所需模块,并给出正确的参数: ⚫ 在 sources 子模块库中选中阶跃输入(step)图标,将其拖入编辑窗口,并用 鼠标左键双击该图标,打开参数设定的对话框,将参数 step time(阶跃时刻) 设为 0。 ⚫ 在 Math(数学)子模块库中选中加法器(sum)图标,拖到编辑窗口中,并双 击该图标将参数 List of signs(符号列表)设为|+-(表示输入为正,反馈为负)。 ⚫ 在 continuous(连续)子模块库中、选积分器(Integrator)和传递函数(Transfer Fcn)图标拖到编辑窗口中,并将传递函数分子(Numerator)改为〔900〕, 分母(Denominator)改为〔1,9〕。 ⚫ 在sinks(输出)子模块库中选择scope(示波器)和Out1(输出端口模块)图标并将 之拖到编辑窗口中。 (3)将画出的所有模块按错误!未找到引用源。用鼠标连接起来,构成一个原系统的 框图描述如图2- 5所示。 (4)选择仿真算法和仿真控制参数,启动仿真过程。 ● 在编辑窗口中点击 Simulation|Simulation parameters 菜单,出现参数对话框,在 solver 模板中设置响应的仿真范围 StartTime(开始时间)和 StopTime(终止时间),仿
自动控制原理实验指导书 真步长范围Maxinum step size(最大步长)和Mininum step size(最小步长)。对于本 例,StopTime可设置为2。最后点击SimulationStart菜单或点击相应的热键启动 仿真。双击示波器,在弹出的图形上会“实时地”显示出仿真结果。输出结果如 图2-7所示。 间untiti1ed米 ✉回☒ Eile Edit View Simulation Format Tools Help D它日母多自鱼22■Norm g00 5钟9 Integrator Transfer Fon Scope 1 Ready 100% ode45 图2-5二阶系统的simulink实现 Scope 回☒ i:W61国 可☒ Zile gdit yiev Insert Taols Mindes Help 吾閨D②热园© D3日凸A/®P0 05 05 1.5 图2-6仿真结果示波器显示 图2-7 MATLAB命令得出的系统响应曲线 命令窗口中键入whos命令,会发现工作空间中增加了两个变量一一tout和yout, 这是因为Simulink中的Outl模块自动将结果写到了MATLAB的工作空间中。利用 MATLAB命令plot(tout,yout),可将结果绘制出来,如错误未找到引用源。所示。比较 图2-7和错误!未找到引用源。,可以发现这两种输出结果是完全一致的。 三、实验能力要求 (1)熟练使用各种函数命令建立控制系统数学模型。 (2)完成实验的范例题和自我实践,并记录结果。 13
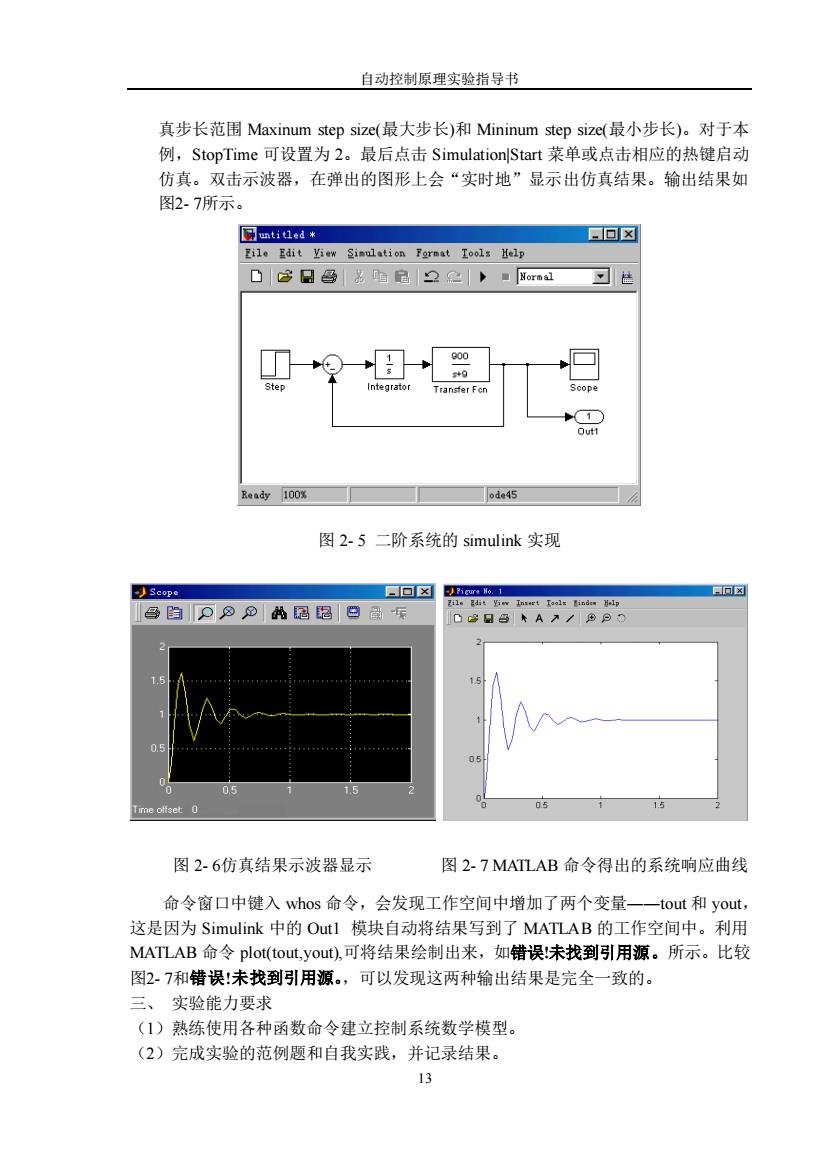
自动控制原理实验指导书 13 真步长范围 Maxinum step size(最大步长)和 Mininum step size(最小步长)。对于本 例,StopTime 可设置为 2。最后点击 Simulation|Start 菜单或点击相应的热键启动 仿真。双击示波器,在弹出的图形上会“实时地”显示出仿真结果。输出结果如 图2- 7所示。 图 2- 5 二阶系统的 simulink 实现 图 2- 6仿真结果示波器显示 图 2- 7 MATLAB 命令得出的系统响应曲线 命令窗口中键入 whos 命令,会发现工作空间中增加了两个变量――tout 和 yout, 这是因为 Simulink 中的 Out1 模块自动将结果写到了 MATLAB 的工作空间中。利用 MATLAB 命令 plot(tout,yout),可将结果绘制出来,如错误!未找到引用源。所示。比较 图2- 7和错误!未找到引用源。,可以发现这两种输出结果是完全一致的。 三、 实验能力要求 (1)熟练使用各种函数命令建立控制系统数学模型。 (2)完成实验的范例题和自我实践,并记录结果

自动控制原理实验指导书 实验三利用MATLAB进行时域分析 一、实验目的 (I)学会使用MATLAB编程绘制控制系统的单位阶跃响应曲线: (2)研究二阶控制系统中,飞、①对系统动态特性和时域指标的影响: (3)掌握准确读取动态特性指标的方法: (4)分析二阶系统闭环极点和闭环零点对系统动态性能的影响: (5)研究三阶系统单位阶跃响应及其动态性能指标与其闭环极点的关系: (6)研究闭环极点和闭环零点对高阶系统动态性能的影响: (⑦了解高阶系统中主导极点与偶极子的作用: (8)了解系统阶跃响应、脉冲响应和斜坡响应输出曲线之间的联系与差别。 二、实验原理及内容 1.求系统的特征根 若已知系统的特征多项式D(S),利用roots()函数可以求其特征根。若已知系统 的传递函数,利用eig()函数可以直接求出系统的特征根。 2、求系统的闭环根、飞和⊙m 函数damp()可以计算出系统的闭环根、飞和on。 3、零极点分布图 可利用pzmap()函数绘制连续系统的零、极点图,从而分析系统的稳定性,调用 格式为: pzmap(num,den) 【范例3-1】给定传递函数 3s4+2s3+5s2+4s+6 G(s)= s5+3s4+4s3+2s2+7s+2 利用下列命令可自动打开一个图形窗口,显示该系统的零、极点分布图,如图 3-所示。 >>num=3,2,5,4,6]: den=[1,3,4,2,7,2] pzmap(num,den) title(Pole-Zero Map)%图形标题。 14
自动控制原理实验指导书 14 实验三 利用 MATLAB 进行时域分析 一、实验目的 (1) 学会使用 MATLAB 编程绘制控制系统的单位阶跃响应曲线; (2) 研究二阶控制系统中,、n 对系统动态特性和时域指标的影响; (3) 掌握准确读取动态特性指标的方法; (4) 分析二阶系统闭环极点和闭环零点对系统动态性能的影响; (5) 研究三阶系统单位阶跃响应及其动态性能指标与其闭环极点的关系; (6) 研究闭环极点和闭环零点对高阶系统动态性能的影响; (7) 了解高阶系统中主导极点与偶极子的作用; (8) 了解系统阶跃响应、脉冲响应和斜坡响应输出曲线之间的联系与差别。 二、实验原理及内容 1. 求系统的特征根 若已知系统的特征多项式 D (s),利用 roots ( ) 函数可以求其特征根。若已知系统 的传递函数,利用 eig ( ) 函数可以直接求出系统的特征根。 2、求系统的闭环根、 和ωn 函数 damp ( ) 可以计算出系统的闭环根、 和 n。 3、零极点分布图 可利用 pzmap()函数绘制连续系统的零、极点图,从而分析系统的稳定性,调用 格式为: pzmap(num,den) 【范例 3-1】给定传递函数: 3 4 2 7 2 3 2 5 4 6 ( ) 5 4 3 2 4 3 2 + + + + + + + + + = s s s s s s s s s G s 利用下列命令可自动打开一个图形窗口,显示该系统的零、极点分布图,如图 3- 所示。 >> num=[3,2,5,4,6]; den=[1,3,4,2,7,2]; pzmap(num,den) title(¹Pole-Zero Map¹) % 图形标题