
自动控制原理实验指导书 Pole-Zero Map 15 9 05 0 -05 Syster sys Pole:-1.T7-127i Damping 0.813 0 Overshoot (%)125 Frequency (rad/sec)2.18 -15 -1 -05 Real Axis 图3-1 MATLAB函数零、极点分布图 4、求系统的单位阶跃响应 step()函数可以计算连续系统单位阶跃响应(impulse()函数可以计算连续系 统单位脉冲响应): step(ys)或step(sys,t)或step(num,den) 函数在当前图形窗口中直接绘制出系统的单位阶跃响应曲线,对象sys可以由tf (),pk()函数中任何一个建立的系统模型。第二种格式中t可以指定一个仿真终止 时间,也可以设置为一个时间矢量(如t=0:dt:Tfinal,即dt是步长,Tfinal是终止 时刻)。 如果需要将输出结果返回到MATLAB工作空间中,则采用以下调用格式: c=step(sys) 此时,屏上不会显示响应曲线,必须利用plot()命令查看响应曲线。plot可以根据两 个或多个给定的向量绘制二维图形。 25 【范例3-2】已知传递函数为:G(s)= s2+4s+25 利用以下MATLAB命令可得阶跃响应曲线如图3-所示。 >>num=[0,0,25]: den=[1,4,25]: step(num,den) grid%绘制网格线。 title(Unit-Step Response of G(s)=25/(s2+4s+25))%图像标题 15
自动控制原理实验指导书 15 图 3- 1 MATLAB 函数零、极点分布图 4、求系统的单位阶跃响应 step ( ) 函数可以计算连续系统单位阶跃响应(impulse( ) 函数可以计算连续系 统单位脉冲响应): step (sys) 或 step ( sys , t ) 或 step (num , den) 函数在当前图形窗口中直接绘制出系统的单位阶跃响应曲线,对象 sys 可以由 tf ( ),zpk ( ) 函数中任何一个建立的系统模型。第二种格式中 t 可以指定一个仿真终止 时间,也可以设置为一个时间矢量(如 t=0 : dt : Tfinal,即 dt 是步长,Tfinal 是终止 时刻)。 如果需要将输出结果返回到 MATLAB 工作空间中,则采用以下调用格式: c=step(sys) 此时,屏上不会显示响应曲线,必须利用 plot()命令查看响应曲线。plot 可以根据两 个或多个给定的向量绘制二维图形。 【范例 3-2】已知传递函数为: 4 25 25 ( ) 2 + + = s s G s 利用以下 MATLAB 命令可得阶跃响应曲线如图3- 所示。 >> num=[0,0,25]; den=[1,4,25]; step(num,den) grid % 绘制网格线。 title(¹Unit-Step Response of G(s)=25/(s^2+4s+25) ¹) % 图像标题
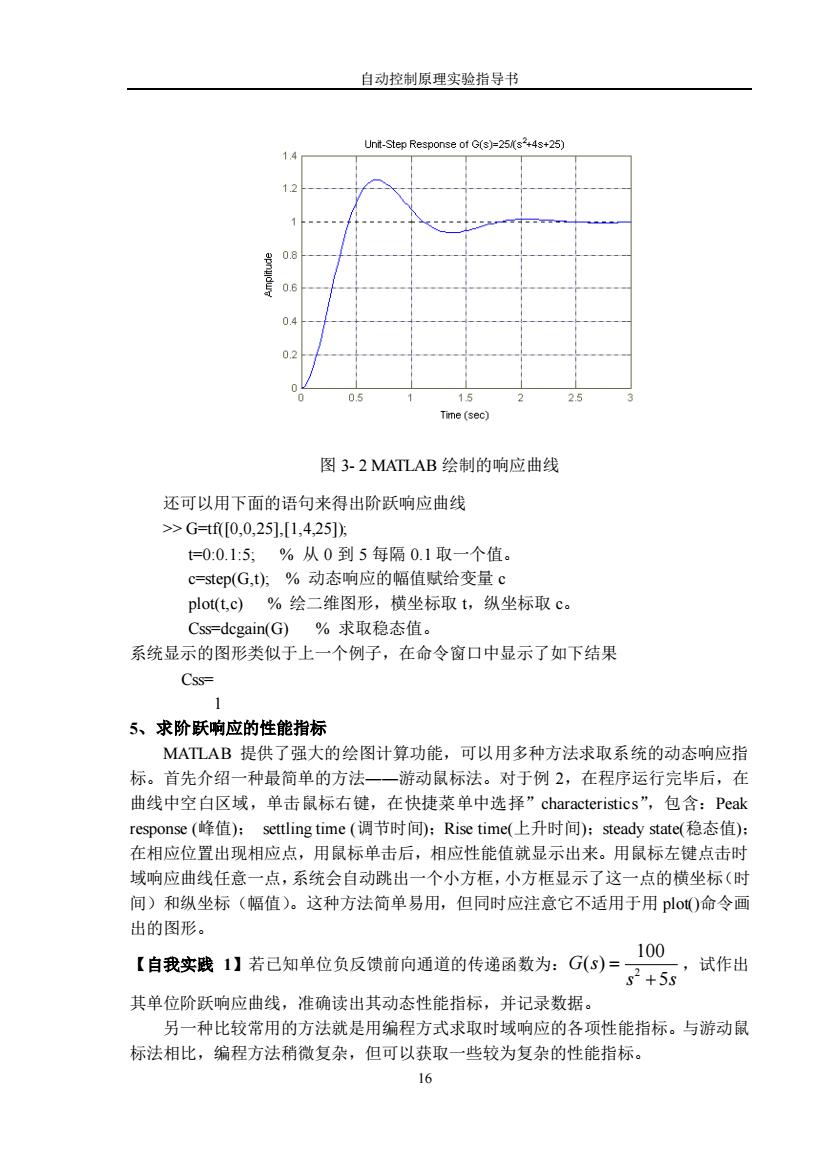
自动控制原理实验指导书 Unit-Step Response of G(s)=25/(s+4s+25) 14 1.2 0.8 0.6 0.4 0.2 0.5 15 Tine(sec】 图3-2 MATLAB绘制的响应曲线 还可以用下面的语句来得出阶跃响应曲线 >G=tf[0,0,25],[1,4,25])月 t=0:0.1:5;%从0到5每隔0.1取一个值。 c=step(G,t),%动态响应的幅值赋给变量c plot(t,c)%绘二维图形,横坐标取t,纵坐标取c。 Css=dcgain(G)%求取稳态值。 系统显示的图形类似于上一个例子,在命令窗口中显示了如下结果 Css= 1 5、求阶跃响应的性能指标 MATLAB提供了强大的绘图计算功能,可以用多种方法求取系统的动态响应指 标。首先介绍一种最简单的方法一一游动鼠标法。对于例2,在程序运行完毕后,在 曲线中空白区域,单击鼠标右键,在快捷菜单中选择”characteristics”,包含:Peak response(峰值):settling time(调节时间):Rise time(上升时间):steady state(稳态值): 在相应位置出现相应点,用鼠标单击后,相应性能值就显示出来。用鼠标左键点击时 域响应曲线任意一点,系统会自动跳出一个小方框,小方框显示了这一点的横坐标(时 间)和纵坐标(幅值)。这种方法简单易用,但同时应注意它不适用于用plo)命令画 出的图形。 100 【自我实践1】若己知单位负反馈前向通道的传递函数为:G(S)= 试作出 s2+5s 其单位阶跃响应曲线,准确读出其动态性能指标,并记录数据。 另一种比较常用的方法就是用编程方式求取时域响应的各项性能指标。与游动鼠 标法相比,编程方法稍微复杂,但可以获取一些较为复杂的性能指标。 16
自动控制原理实验指导书 16 图 3- 2 MATLAB 绘制的响应曲线 还可以用下面的语句来得出阶跃响应曲线 >> G=tf([0,0,25],[1,4,25]); t=0:0.1:5; % 从 0 到 5 每隔 0.1 取一个值。 c=step(G,t); % 动态响应的幅值赋给变量 c plot(t,c) % 绘二维图形,横坐标取 t,纵坐标取 c。 Css=dcgain(G) % 求取稳态值。 系统显示的图形类似于上一个例子,在命令窗口中显示了如下结果 Css= 1 5、求阶跃响应的性能指标 MATLAB 提供了强大的绘图计算功能,可以用多种方法求取系统的动态响应指 标。首先介绍一种最简单的方法――游动鼠标法。对于例 2,在程序运行完毕后,在 曲线中空白区域,单击鼠标右键,在快捷菜单中选择”characteristics”,包含:Peak response (峰值); settling time (调节时间);Rise time(上升时间);steady state(稳态值); 在相应位置出现相应点,用鼠标单击后,相应性能值就显示出来。用鼠标左键点击时 域响应曲线任意一点,系统会自动跳出一个小方框,小方框显示了这一点的横坐标(时 间)和纵坐标(幅值)。这种方法简单易用,但同时应注意它不适用于用 plot()命令画 出的图形。 【自我实践 1】若已知单位负反馈前向通道的传递函数为: 2 100 ( ) 5 G s s s = + ,试作出 其单位阶跃响应曲线,准确读出其动态性能指标,并记录数据。 另一种比较常用的方法就是用编程方式求取时域响应的各项性能指标。与游动鼠 标法相比,编程方法稍微复杂,但可以获取一些较为复杂的性能指标

自动控制原理实验指导书 若将阶跃响应函数step()获得系统输出量返回到变量y中,可以调用如下格式 [y,t]=step(G) 该函数还同时返回了自动生成的时间变量t,对返回变量y和t进行计算,可以得 到时域性能指标。 ①峰值时间(timetopeak)可由以下命令获得: [Y,k]=maxy)方 timetopeak=t(k) ②最大(百分比)超调量(percentovershoot)可由以下命令得到: C=dcgain(G); [Y,k]=max(y); percentovershoot=100*(Y-C)/C dcgain()函数用于求取系统的终值。 ③上升时间(risetime)可利用MATLAB中控制语句编制M文件来获得。 要求出上升时间,可以用while语句编写以下程序得到: C=dcgain(G); n=1; while y(n)<C n=n+l; end risetime=t(n) 在阶跃输入条件下,y的值由零逐渐增大,当以上循环满足yC时,退出循环, 此时对应的时刻,即为上升时间。 对于输出无超调的系统响应,上升时间定义为输出从稳态值的10%上升到90%所 需时间,则计算程序如下: C=dcgain(G); n=1; while y(n)<0.1*C n=n+1; end m=l1; while y(n)<0.9*C m=m+1; end risetime=t(m)-t(n) ④调节时间(setllingtime)可由while语句编程得到: C=dcgain(G); i=length(t); while(y(i>0.98*C)&(y(i)<1.02*C) 17
自动控制原理实验指导书 17 若将阶跃响应函数 step( )获得系统输出量返回到变量 y 中,可以调用如下格式 [y,t]=step(G) 该函数还同时返回了自动生成的时间变量 t,对返回变量 y 和 t 进行计算,可以得 到时域性能指标。 ① 峰值时间(timetopeak)可由以下命令获得: [Y,k]=max(y); timetopeak=t(k) ② 最大(百分比)超调量(percentovershoot)可由以下命令得到: C=dcgain(G); [Y,k]=max(y); percentovershoot=100*(Y-C)/C dcgain( )函数用于求取系统的终值。 ③ 上升时间(risetime)可利用 MATLAB 中控制语句编制 M 文件来获得。 要求出上升时间,可以用 while 语句编写以下程序得到: C=dcgain(G); n=1; while y(n)<C n=n+1; end risetime=t(n) 在阶跃输入条件下,y 的值由零逐渐增大,当以上循环满足 y=C 时,退出循环, 此时对应的时刻,即为上升时间。 对于输出无超调的系统响应,上升时间定义为输出从稳态值的 10%上升到 90%所 需时间,则计算程序如下: C=dcgain(G); n=1; while y(n)<0.1*C n=n+1; end m=1; while y(n)<0.9*C m=m+1; end risetime=t(m)-t(n) ④ 调节时间(setllingtime)可由 while 语句编程得到: C=dcgain(G); i=length(t); while(y(i)>0.98*C)&(y(i)<1.02*C)

自动控制原理实验指导书 i=i-1; end setllingtime=t(i) 用向量长度函数length()可求得t序列的长度,将其设定为变量i的上限值。 3 【范例3-3】己知二阶系统传递函数为:G(s)= (s+1-3i)(s+1+3i) 利用下面的stepanalysis.m程序可得到阶跃响应如图3-及性能指标数据。 >G=Zφk([],-1+3*i,-1-3*i],3)月 %计算最大峰值时间和超调量。 C=dcgain(G) [y,t]=step(G); plot(t,y) grid [Y,k]=maxy)方 timetopeak=t(k) percentovershoot=100*(Y-C)/C %计算上升时间。 n=1; while y(n)<C n=n+l; end risetime=t(n) %计算调节时间。 i=length(t); while(y(i)>0.98*C)&(y(iK1.02*C) i=i-1; end setllingtime=t(i) 运行后的响应图如图3-,命令窗口中显示的结果为 C= timetopeak 0.3000 1.0491 percentovershoot risetime 35.0914 0.6626 setllingtime 3.5337 18
自动控制原理实验指导书 18 i=i-1; end setllingtime=t(i) 用向量长度函数 length( )可求得 t 序列的长度,将其设定为变量 i 的上限值。 【范例 3-3】已知二阶系统传递函数为: ( 1 3 )( 1 3 ) 3 ( ) s i s i G s + − + + = 利用下面的 stepanalysis.m 程序可得到阶跃响应如图3-及性能指标数据。 >> G=zpk([ ],[-1+3*i,-1-3*i ],3); % 计算最大峰值时间和超调量。 C=dcgain(G) [y,t]=step(G); plot(t,y) grid [Y,k]=max(y); timetopeak=t(k) percentovershoot=100*(Y-C)/C % 计算上升时间。 n=1; while y(n)<C n=n+1; end risetime=t(n) % 计算调节时间。 i=length(t); while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1; end setllingtime=t(i) 运行后的响应图如图3-,命令窗口中显示的结果为 C = timetopeak = 0.3000 1.0491 percentovershoot = risetime = 35.0914 0.6626 setllingtime = 3.5337
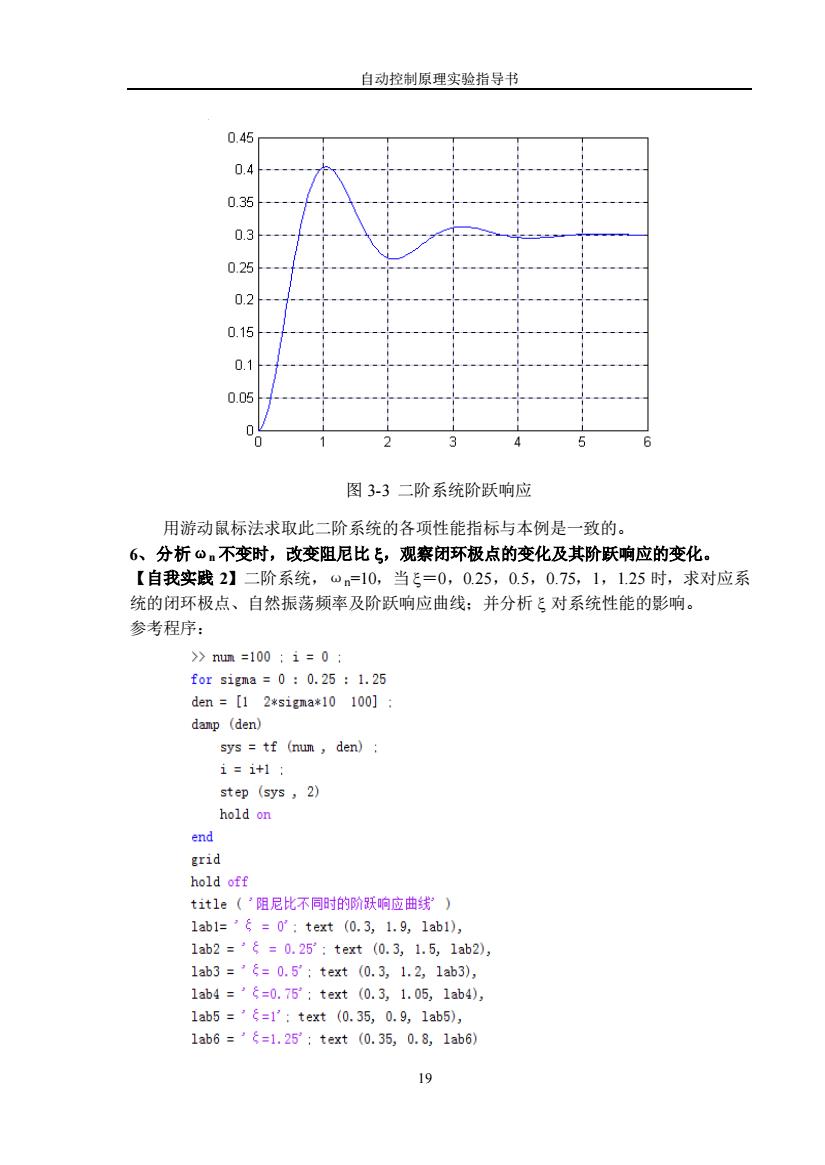
自动控制原理实验指导书 0.45 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 图3-3二阶系统阶跃响应 用游动鼠标法求取此二阶系统的各项性能指标与本例是一致的。 6、分析o不变时,改变阻尼比飞,观察闭环极点的变化及其阶跃响应的变化。 【自我实践2】二阶系统,om=10,当ξ=0,0.25,0.5,0.75,1,1.25时,求对应系 统的闭环极点、自然振荡频率及阶跃响应曲线:并分析飞对系统性能的影响。 参考程序: >num=100:i=0: for sigma=0:0.25:1.25 den=[12*s1gma*10100]: damp (den) sys tf (num den); i=i+1: step (sys,2) hold on end grid hold off tit1e(阻尼比不同时的阶跃响应曲线) 1ab1=’ξ=0°:text(0.3,1.9,1ab1), 1ab2=°=0.25°:text(0.3,1.5,1ab2) 1ab3=’=0.5:text(0.3,1.2,1ab3), 1ab4=’ξ=0.75:text(0.3,1.05,1ab4), 1ab5=’=1:text(0.35,0.9,1ab5), 1ab6=ξ=1.25;text(0.35,0.8,1ab6) 19
自动控制原理实验指导书 19 图 3-3 二阶系统阶跃响应 用游动鼠标法求取此二阶系统的各项性能指标与本例是一致的。 6、分析ωn 不变时,改变阻尼比 ,观察闭环极点的变化及其阶跃响应的变化。 【自我实践 2】二阶系统,ωn=10,当 =0,0.25,0.5,0.75,1,1.25 时,求对应系 统的闭环极点、自然振荡频率及阶跃响应曲线;并分析 对系统性能的影响。 参考程序: