
自动控制原理实验指导书 其中Mp=e ,,=。 4,c,)=1+e Co 2)典型三阶系统在不同开环增益下的响应情况 表1-2 R(K2) 开环增益K 稳定性 表1-3 R(K2) 开环增益K 稳定性 30 16.7 不稳定发散 41.7 12 临界稳定等幅振荡 100 5 稳定衰减收敛 注意:在做实验前一定要进行对象整定,否则将会导致理论值和实际测量值相差 较大。 5
自动控制原理实验指导书 5 其中 2 1 Mp e − − = , 2 n p 1 t − = , n s 4 t = , 2 1 p C(t ) 1 e − − = + 2)典型三阶系统在不同开环增益下的响应情况 表 1-2 R(KΩ) 开环增益 K 稳定性 表 1-3 R(KΩ) 开环增益 K 稳定性 30 16.7 不稳定发散 41 .7 12 临界稳定等幅振荡 100 5 稳定衰减收敛 注意:在做实验前一定要进行对象整定,否则将会导致理论值和实际测量值相差 较大

自动控制原理实验指导书 实验二用MATLAB建立传递函数模型 一、实验目的 (1)熟悉MATLAB实验环境,掌握MATLAB命令窗口的基本操作: (2)掌握MATLAB建立控制系统数学模型的命令及模型相互转换的方法: (3)掌握使用MATLAB命令化简模型基本连接的方法: (4)学会使用Simulink模型结构图化简复杂控制系统模型的方法。 二、实验原理及内容 控制系统常用的数学模型有四种:传递函数模型(tf对象)、零极点增益模型(zpk 对象)、结构框图模型和状态空间模型($s对象)。经典控制理论中数学模型一般使用 前三种模型,状态空间模型属于现代控制理论范畴。 1、有理函数棋型 线性连续系统的传递函数模型可一般地表示为: G(s)=bis"tbbs+bm n2m (10) s”+asm-+…+an-1S+an 将系统的分子和分母多项式的系数按降幂的方式以向量的形式输入给两个变量 mm和den,就可以轻易地将传递函数模型输入到MATLAB环境中。命令格式为: num=[b,62;,bm,bm]; (2) den=[1aaz,aa]. (3) 用函数廿()来建立控制系统的传递函数模型,该函数的调用格式为: G=tf(num,den); (4) 例1一个简单的传递函数模型: 5+5 Gs)=g÷+252+3s2+4s+5 可以由下面的命令输入到MATLAB工作空间中去。 >num=[1,2] den=[1,2,3,4,5]; G=tf(num,den) 运行结果: Transfer function: S+2 s4+2s^3+3s^2+4s+5 6
自动控制原理实验指导书 6 实验二 用 MATLAB 建立传递函数模型 一、实验目的 (1)熟悉 MATLAB 实验环境,掌握 MATLAB 命令窗口的基本操作; (2)掌握 MATLAB 建立控制系统数学模型的命令及模型相互转换的方法; (3)掌握使用 MATLAB 命令化简模型基本连接的方法; (4)学会使用 Simulink 模型结构图化简复杂控制系统模型的方法。 二、实验原理及内容 控制系统常用的数学模型有四种:传递函数模型(tf 对象)、零极点增益模型(zpk 对象)、结构框图模型和状态空间模型(ss 对象)。经典控制理论中数学模型一般使用 前三种模型,状态空间模型属于现代控制理论范畴。 1、有理函数模型 线性连续系统的传递函数模型可一般地表示为: n m s a s a s a b s b s b s b G s n n n n m m m m + + + + + + + + = − − + − ( ) 1 1 1 1 1 1 2 (1) 将系统的分子和分母多项式的系数按降幂的方式以向量的形式输入给两个变量 num 和 den ,就可以轻易地将传递函数模型输入到 MATLAB 环境中。命令格式为: [ , , , , ] 1 2 +1 = num b b bm bm ; (2) [1, , , , , ] den a1 a2 an−1 an = ; (3) 用函数 tf ( ) 来建立控制系统的传递函数模型,该函数的调用格式为: G=tf(num,den); (4) 例 1 一个简单的传递函数模型: 2 3 4 5 5 ( ) 4 3 2 + + + + + = s s s s s G s 可以由下面的命令输入到 MATLAB 工作空间中去。 >> num=[1,2]; den=[1,2,3,4,5]; G=tf(num,den) 运行结果: Transfer function: s + 2 ----------------------------- s^4 + 2 s^3 + 3 s^2 + 4 s + 5

自动控制原理实验指导书 这时对象G可以用来描述给定的传递函数模型,作为其它函数调用的变量。 例2一个稍微复杂一些的传递函数模型: 6(s+5) G(s)= (s2+3s+1)2(s+6) >>num=6*[1,5]: den=conv(conv(1,3,1],[1,3,1]),[1,6]) tf(num,den) 运行结果 Transfer function: 6s+30 s^5+12s4+47s3+72s2+37s+6 其中covO函数(标准的MATLAB函数)用来计算两个向量的卷积,多项式乘 法也可以用这个函数来计算。该函数允许任意地多层嵌套,从而表示复杂的计算。 5 【自我实践1】建立控制系统的传递函数模型:G(S)= s(s+1)(s2+4s+4) 2、零极点棋型 线性系统的传递函数还可以写成极点的形式: Gy)=KS+s+32)…s+m) (s+p)(s+p2).(s+P) 将系统增益K、零点-z和极点-p以向量的形式输入给三个变量KGa、Z和P, 命令格式为: KGain =K: (6) Z=[-2-22…-2m3 (7) P=[-P-P2:…;-Pn} (8) 用函数命令z印k()来建立系统的零极点增益模型,其函数调用格式为: G=zpk(Z,P,KGain) (9) 例3某系统的零极点模型为: G(s)=6 (s+1.9294)(s+0.0353±0.9287) (s+0.9567±1.2272j)(s-0.0433±0.6412j) >> KGain=6;
自动控制原理实验指导书 7 这时对象 G 可以用来描述给定的传递函数模型,作为其它函数调用的变量。 例 2 一个稍微复杂一些的传递函数模型: ( 3 1) ( 6) 6( 5) ( ) 2 2 + + + + = s s s s G s >> num=6*[1,5]; den=conv(conv([1,3,1],[1,3,1]),[1,6]); tf(num,den) 运行结果 Transfer function: 6 s + 30 ----------------------------------------- s^5 + 12 s^4 + 47 s^3 + 72 s^2 + 37 s + 6 其中 conv()函数(标准的 MATLAB 函数)用来计算两个向量的卷积,多项式乘 法也可以用这个函数来计算。该函数允许任意地多层嵌套,从而表示复杂的计算。 【自我实践 1】建立控制系统的传递函数模型: 2 5 ( ) ( 1)( 4 4) G s s s s s = + + + 2、零极点模型 线性系统的传递函数还可以写成极点的形式: ( )( ) ( ) ( )( ) ( ) ( ) 1 2 1 2 n m s p s p s p s z s z s z G s K + + + + + + = 将系统增益 K、零点-zi 和极点-pj 以向量的形式输入给三个变量 KGain、Z 和 P, 命令格式为: KGain = K; (6) Z = [−z1;− z2;;− zm ]; (7) P = [−p1;− p2;;− pn ]; (8) 用函数命令 zpk ( ) 来建立系统的零极点增益模型,其函数调用格式为: G=zpk(Z,P,KGain) (9) 例 3 某系统的零极点模型为: ( 0.9567 1.2272 )( 0.0433 0.6412 ) ( 1.9294)( 0.0353 0.9287 ) ( ) 6 s j s j s s j G s + − + + = >> KGain=6;

自动控制原理实验指导书 z=[-1.9294;-0.0353+0.9287j-0.0353-0.9287j p=[-0.9567+1.2272j;-0.9567-12272j:0.0433+0.6412j:0.0433-0.6412j: G=zpk(z,p,KGain) 运行结果 Zero/pole/gain: 6(s+1.929)(s2+0.0706s+0.8637) (s2-0.0866s+0.413)(s^2+1.913s+2.421) 注意:对于单变量系统,其零极点均是用列向量来表示的,故Z、P向量中各项 均用分号(;)隔开。 【自我实践2】建立控制系统的零极点模型:G(S)= 8(s+1-j)(s+1+j) s2(s+5(s+6)s2+1) 3、控制系统棋型间的相互转换 零极点模型转换为传递函数模型:[num,den]=zp2tf(Z,p,k) 传递函数模型转化为零极点模型:[z,p,k]=tf2z印(num,den) 例4给定系统传递函数为: 6.8s2+61.2s+95.2 G(s)=- 4+7.5s3+22s2+19.5 对应的零极点模型可由下面的命令得出 >>num=[6.8,61.2,95.2] den=[1,7.5,22,19.5,0]; G=tf(num,den); Gl=zpk(G) 显示结果: Zero/pole/gain: 6.8(s+7)(s+2) s(s+1.5)(s^2+6s+13) 可见,在系统的零极点模型中若出现复数值,则在显示时将以二阶因子的形式表 示相应的共轭复数对。 例5给定零极点模型: G(s)=6.8 (S+2)(S+7) s(s+3±2)(s+1.5) 可以用下面的MATLAB命令立即得出其等效的传递函数模型。输入程序时要注 意大小写
自动控制原理实验指导书 8 z=[-1.9294;-0.0353+0.9287j;-0.0353-0.9287j]; p=[-0.9567+1.2272j;-0.9567-1.2272j;0.0433+0.6412j;0.0433-0.6412j]; G=zpk(z,p,KGain) 运行结果: Zero/pole/gain: 6 (s+1.929) (s^2 + 0.0706s + 0.8637) --------------------------------------------------------- (s^2 - 0.0866s + 0.413) (s^2 + 1.913s + 2.421) 注意:对于单变量系统,其零极点均是用列向量来表示的,故 z、p 向量中各项 均用分号(;)隔开。 【自我实践 2】建立控制系统的零极点模型: 2 2 8( 1 )( 1 ) ( ) ( 5)( 6)( 1) s j s j G s s s s s + − + + = + + + 3、控制系统模型间的相互转换 零极点模型转换为传递函数模型:[num , den] = zp2tf ( z, p, k ) 传递函数模型转化为零极点模型:[z , p , k] = tf2zp ( num, den ) 例 4 给定系统传递函数为: s s s s s s G s 7.5 22 19.5 6.8 61.2 95.2 ( ) 4 3 2 2 + + + + + = 对应的零极点模型可由下面的命令得出 >> num=[6.8, 61.2, 95.2]; den=[1, 7.5, 22, 19.5, 0]; G=tf(num,den); G1=zpk(G) 显示结果: Zero/pole/gain: 6.8 (s+7) (s+2) ------------------------------ s (s+1.5) (s^2 + 6s + 13) 可见,在系统的零极点模型中若出现复数值,则在显示时将以二阶因子的形式表 示相应的共轭复数对。 例 5 给定零极点模型: ( 3 2)( 1.5) ( 2)( 7)) ( ) 6.8 + + + + = s s j s s s G s 可以用下面的 MATLAB 命令立即得出其等效的传递函数模型。输入程序时要注 意大小写
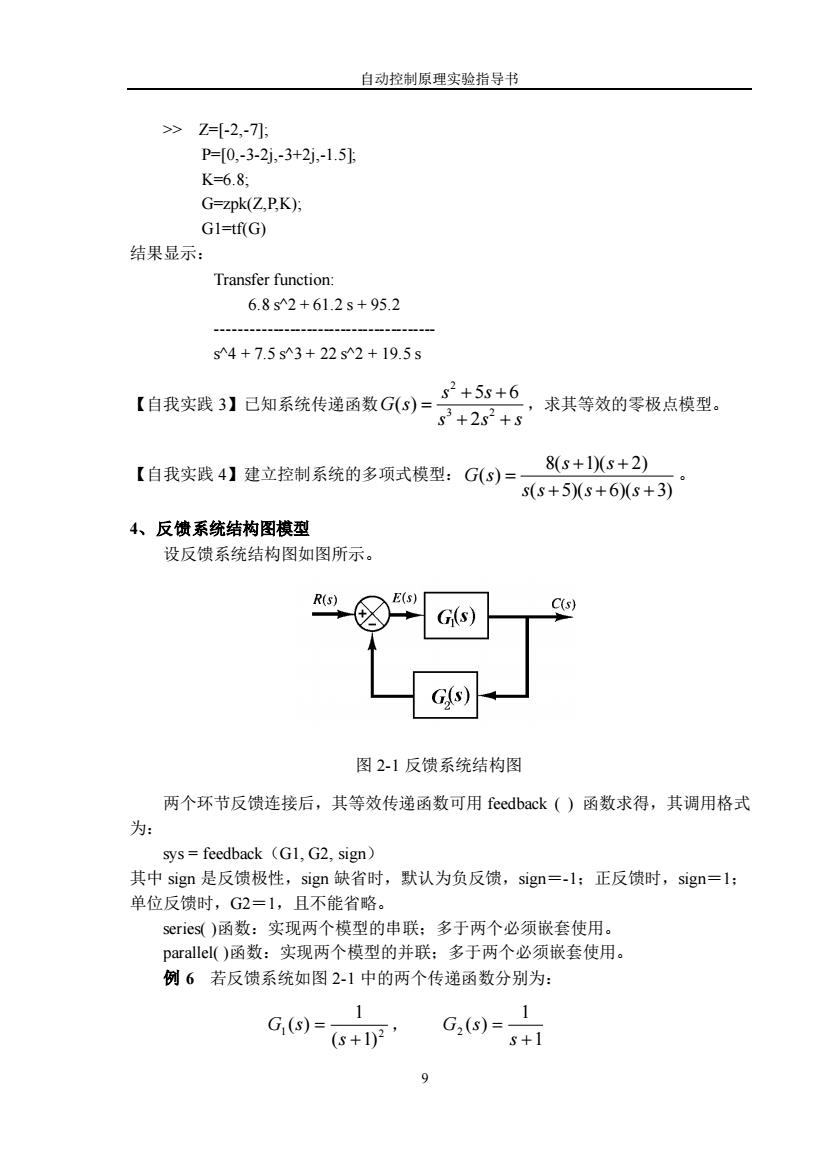
自动控制原理实验指导书 >> Z=[-2,-7 P=[0,-3-2j,-3+2j,-1.5 K=6.8 G=zpk(Z,P,K); G1=tf(G) 结果显示: Transfer function: 6.8s^2+61.2s+95.2 s^4+7.5s3+22s^2+19.5s s2+5s+6 【自我实践3】已知系统传递函数G(S)= ,求其等效的零极点模型。 53+252+ 【自我实践4】建立控制系统的多项式模型:G(s)= 8(s+1)(s+2) s(s+5)(s+6)(s+3) 4、反馈系统结构图模型 设反馈系统结构图如图所示。 R(s) E(s) C(s) G(s) 图2-1反馈系统结构图 两个环节反馈连接后,其等效传递函数可用feedback()函数求得,其调用格式 为: sys=feedback (G1,G2,sign) 其中sign是反馈极性,sign缺省时,默认为负反馈,sign=-l;正反馈时,sign=1; 单位反馈时,G2=1,且不能省略。 series()函数:实现两个模型的串联;多于两个必须嵌套使用。 parallel()函数:实现两个模型的并联:多于两个必须嵌套使用。 例6若反馈系统如图2-1中的两个传递函数分别为: 1 G(s)= (8+102, G2(s)= +1 9
自动控制原理实验指导书 9 >> Z=[-2,-7]; P=[0,-3-2j,-3+2j,-1.5]; K=6.8; G=zpk(Z,P,K); G1=tf(G) 结果显示: Transfer function: 6.8 s^2 + 61.2 s + 95.2 --------------------------------------- s^4 + 7.5 s^3 + 22 s^2 + 19.5 s 【自我实践 3】已知系统传递函数 2 3 2 5 6 ( ) 2 s s G s s s s + + = + + ,求其等效的零极点模型。 【自我实践 4】建立控制系统的多项式模型: 8( 1)( 2) ( ) ( 5)( 6)( 3) s s G s s s s s + + = + + + 。 4、反馈系统结构图模型 设反馈系统结构图如图所示。 图 2-1 反馈系统结构图 两个环节反馈连接后,其等效传递函数可用 feedback ( ) 函数求得,其调用格式 为: sys = feedback(G1, G2, sign) 其中 sign 是反馈极性,sign 缺省时,默认为负反馈,sign=-1;正反馈时,sign=1; 单位反馈时,G2=1,且不能省略。 series( )函数:实现两个模型的串联;多于两个必须嵌套使用。 parallel( )函数:实现两个模型的并联;多于两个必须嵌套使用。 例 6 若反馈系统如图 2-1 中的两个传递函数分别为: 1 2 ( 1) 1 ( ) + = s G s , 1 1 ( ) 2 + = s G s