
《大学物理》作业No.3波的干涉一、选择题1.如图所示,S,和S,为两相干波源,它们的振动方向均垂直于图面,发出波长为的简谐波。P点是两列波相遇区域中的一点,已知S,P=2元,S,P=2.2,两列波在P点发生相消干涉。若S,的振动方程为=Acos(2元1+元),,则 S,Sio的振动方程为[D](A) y= Acos(2 元1 -n)5.(B) y2 = Acos(2 元 t - 元)(C) y2 = Acos(2 元1 +≥元)(D) y2 = Acos(2 元t - 0.1 元)解:S和S,在P点发生相消干涉,相位差为Ap=2-9-32(r2 -)=(2k +1)元(-)=(2k+1)+元+(2.24-2)02 =(2k +1)元 + 91 + 2元=2k元+1%令k=-1,则9:=-元。因为和片在P点发生相消干涉,A=4=4,所以,S,的振动方程为J2=Acos(2元1-元)= Acos(2元1-0.1元)102.有两列沿相反方向传播的相干波,其波动方程分别为y=Acos2元(vt-x/2)和y2=Acos2元(vt+x/),叠加后形成驻波,其波腹位置的坐标为:【C](B) x=±号(2k+1)a(A) x=±ka(C) x=±ka(D)x=+(2k+1)a其中的k=0,1,2,3
《大学物理》作业 No.3 波的干涉 一、选择题 1.如图所示, 1 S 和 2 S 为两相干波源,它们的振动方向均垂直于图面, 发出波长为的简谐 波。P 点是两列波相遇区域中的一点,已知 S1P = 2 , S2P = 2.2 ,两列波在 P 点发生 相消干涉。若 1 S 的振动方程为 ) 2 1 cos(2 y1 = A t + , 则 2 S 的振动方程为[ D ] ) 2 1 (A) y2 = Acos( 2 t − (B) cos( 2 ) y2 = A t − ) 2 1 (C) y2 = Acos( 2 t + (D) cos(2 0.1 ) y2 = A t − 解:S1 和 2 S 在 P 点发生相消干涉,相位差为 ( ) (2 1) 2 = 2 − 1 − r2 − r1 = k + ( ) 2 (2 1) 2 1 2 1 = k + + + r − r (2.2 2 ) 2 2 1 (2 1) = k + + + − 10 19 = 2k + 令 10 1 1 , k = − 则 2 = − 。因为 y1 和 y2 在 P 点发生相消干涉, A2 = A1 = A, 所以, 2 S 的振动方程为 ) cos( 2 0.1 ) 10 1 y2 = Acos( 2 t − = A t − 2.有两列沿相反方向传播的相干波,其波动方程分别为 cos2 ( / ) y1 = A vt − x 和 cos2 ( / ) y2 = A vt + x ,叠加后形成驻波,其波腹位置的坐标为:[ C ] (A) x = k (2 1) 2 1 (B) x = k + x k 2 1 (C) = (2 1) 4 1 (D) x = k + 其中的 k = 0, 1, 2, 3 1 S P 2 S

解:两列波叠加后形成驻波,其方程为y=y+=2Acos(2元)cos(x)波腹处有:cos()=±1,所以×=±,ka某时刻驻波波形曲线如图所示,则a、b两点的位相差是[A(B) 1元(A) 元(C) 元元(D) 0解:a、b为驻波波节c点两侧的点,则振动相位相反,位相差为元。在弦线上有一简谐波,其表达式是1=2.0×10-2cos[2元(1/0.02-x/20)+ 元/3] (SI)3.为了在此弦线上形成驻波,并且在x=0处为一波节,此弦线上还应有一简谐波,其表达式为:【](A) y, =2.0×10- cos[2元(t/0.02 +x/20) +元/3] (SI)(B) y,=2.0×10~ cos[2元(t/0.02+x/20)+2元/3] (SI)(C)y,=2.0×10- cos[2元(t/0.02+x/20)+4元/3] (SI)(D) J2=2.0×10-~ cos[2元(t/0.02+x/20)-元/3] (SI)解:据驻波形成条件设另一简谐波的波动方程为:20×10~cos2(2)]由题意,×=0处为波节,则=,==元,所以0.一元+号-年个=20×10~cos[2(002)+]4.若在弦上的驻波表达式是y=0.20 sin 2元xcos 20元1(S ID)。则形成该驻波的两个反向行进的行波为:[℃]
解:两列波叠加后形成驻波,其方程为 ) 2 2 cos(2 ) cos( 1 2 y y y A t x = + = 波腹处有: ) 1 2 cos( x = ,所以 x k 2 1 = 某时刻驻波波形曲线如图所示,则 a、b 两点的位相差是[ A ] (A) 2 1 (B) 4 5 (C) (D) 0 解:a 、b 为驻波波节 c 点两侧的点,则振动相位相反,位相差为 。 在弦线上有一简谐波,其表达式是 2.0 10 cos[ 2 ( / 0.02 / 20) / 3 ] (SI) 2 1 = − + − y t x 3.为了在此弦线上形成驻波,并且在 x = 0 处为一波节,此弦线上还应有一简谐波,其表 达式为:[ C ] (A) 2.0 10 cos[ 2 ( / 0.02 / 20) / 3 ] (SI) 2 2 = + + − y t x (B) 2.0 10 cos[ 2 ( / 0.02 / 20) 2 / 3 ] (SI) 2 2 = + + − y t x (C) 2.0 10 cos[ 2 ( / 0.02 / 20) 4 / 3 ] (SI) 2 2 = + + − y t x (D) 2.0 10 cos[ 2 ( / 0.02 / 20) / 3 ] (SI) 2 2 = + − − y t x 解:据驻波形成条件设另一简谐波的波动方程为: ) ] 0.02 20 2.0 10 cos[2 ( 2 2 2 = + + − t x y 由题意, x = 0 处为波节,则 = − = − = 3 2 1 2 ,所以 3 4 3 2 = + = ] 3 4 ) 0.02 20 2.0 10 cos[2 ( 2 2 = + + − t x y 4.若在弦上的驻波表达式是 y = 0.20 sin 2 x cos 20 t (S I)。则形成该驻波的两个反向 行进的行波为:[ C ] A a b 2 x y c O − A

(A)=0.10 cos[2元(101-x)+] ;=0.10 cos[2(101+x)+] (SI)(B) y=0.1 cos[2(101-x)-]=0.10cos[2元(101+x)+]) (SI)(C) ,=0.10 cos[2元(10t-x)+]=0.10cos[2元(101+x)-] (SI)(D) y1=0.10 cos[2元(10t-x)+二元]J2=0.10 cos[2元(101+x)+] (SI)解: 对(C) J=+y2=0.20cos(2x-)cos(20ml)= 0.20 sin(2x)cos(20ml)二、填空题1.在截面积为S的圆管中,有一列平面简谐波在传播,其波的表达为y=Acos(o1-2元/)管中波的平均能量密度是w,则通过截面积 S的平均能流是sw。2元解:由平均能流密度和平均能流的定义,平均能流为Pww.S1-w-s-ws-sw212.两相干波源S,和S,的振动方程分别是J=AcosOt和y2=Acos(の1+S,距P点3个波长,S,距P点21/4个波长。两波在P点引起的两个振动的相位差的纯对值是4元。解:两相干波在P点的相位差为=0:-0-(5-n)元-0-(-3)-4元[Ag = 4元M3.S,S,为振动频率、振动方向均相同的两个点波源,振动方s"向垂直纸面,两者相距(a为波长)如图。已知S,的初相位N为元。(1)若使射线S,C上各点由两列波引起的振动均干涉相消,则S,的初位相应为:
] 2 1 (A) 0.10 cos[2 (10 ) y1 = t − x + ] (SI) 2 1 0.10 cos[ 2 (10 ) y2 = t + x + ] 4 (B) 0.10 cos[ 2 (10 ) 1 y = t − x − ] (SI) 4 3 0.10 cos[ 2 (10 ) y2 = t + x + ] 2 1 (C) 0.10 cos[2 (10 ) y1 = t − x + ] (SI) 2 1 0.10 cos[2 (10 ) y2 = t + x − ] 4 3 (D) 0.10 cos[ 2 (10 ) y1 = t − x + ] (SI) 4 3 0.10 cos[2 (10 ) y2 = t + x + 解: 对(C) ) cos(20 ) 0.20sin( 2 ) cos(20 ) 2 y y1 y2 0.20cos(2 x t x t = + = − = 二、填空题 1.在截面积为 S 的圆管中,有一列平面简谐波在传播,其波的表达为 ) 2 cos ( x y = A t − , 管中波的平均能量密度是 w, 则通过截面积 S 的平均能流是 Sw 2 。 解:由平均能流密度和平均能流的定义,平均能流为 S w S S w T P = wu S = w = = ⊥ 2 2 2. 两相干波源 1 S 和 2 S 的振动方程分别是 y Acost 1 = 和 ) 2 1 cos( y2 = A t + 。 1 S 距 P 点 3 个波长, 2 S 距 P 点 21/ 4 个波长。两波在 P 点引起的两个振动的相位差的绝 对值是 4 。 解:两相干波在 P 点的相位差为: 3 ) 4 4 21 ( 2 0 2 1 ( ) 2 = 2 − 1 − r2 − r1 = − − − = − = 4 3. 1 2 S , S 为振动频率、振动方向均相同的两个点波源,振动方 向垂直纸面,两者相距 2 3 (为波长) 如图。已知 1 S 的初相位 为 2 1 。 (1) 若使射线 S2 C 上各点由两列波引起的振动均干涉相消,则 2 S 的初位相应为: • • • M N S1 2 S C

2k元+元/2,k =0,±1, ±2,...(2)若使S,S,连线的中垂线MN上各点由两列波引起的振动均干涉相消,则S,的初位相应为:2k元+3元/2,k=0,±1,±2,…解:(1)在S外侧C点,两列波的相位差为:(μ-r)=02-号-(号2)=(2+1)元A= --2-元92=2k元+元/2,(k=0,±1,±2,-)(2)在S,S,中垂线上任一点,若产生相消干涉,则2元T=(2k+1)元Ap=02-91 -(r -n)=@2 -P2=2k元+3元/2,(k=0,±1, ±2,*-)4.设入射波的表达式为y=Acos2元(vt+)。波在×=0处发生反射,反射点为固定端,则形成的驻波表达为y=2Acos(2元x/-元)cos(2元vt+元)或y=2Acos (2元x/α+元)cos(2元v1-元)解:1=Acos(2元V1+2元)=Acos(2元V1-+2元号+22反射波在x=0处有半波损失,令,=Acos(2元V1-2元)=Acos[2V1-号-(2元+)合成驻波方程为:=+=24cos(2+)cos(2m1-或者:将写成Acos(2+2元x/2)=Aos(2v1++2反波为Aos(22元+)=40os2→-(2合成驻波方程为:y=+=2Acos(2元)cos(2m1+)2
2k + / 2 , k = 0, 1, 2 , 。 (2) 若使 S1 S2 连线的中垂线 M N 上各点由两列波引起的振动均干涉相消,则 2 S 的 初位相应为: 2k + 3 / 2 , k = 0, 1, 2 , 解:(1) 在 2 S 外侧 C 点,两列波的相位差为: ( ) 2 2 1 2 1 = − − r − r ) (2 1) 2 3 ( 2 2 = 2 − − − = k + 2 / 2 ,( 0, 1, 2 , ) 2 = k + k = (2) 在 S1S2 中垂线上任一点,若产生相消干涉,则 (2 1) 2 ( ) 2 = 2 − 1 − r2 − r1 = 2 − = k + 2 3 / 2 ,( 0, 1, 2 , ) 2 = k + k = 4. 设入射波的表达式为 cos 2 ( ) 1 x y = A v t + 。 波在 x = 0 处发生反射,反射点为固 定端,则形成的驻波表达为 ) 2 1 ) cos( 2 2 1 y = 2 A cos ( 2 x / − v t + ) 2 1 ) cos( 2 2 1 或 y = 2 A cos ( 2 x / + v t − 。 解: ) 2 2 2 1 cos ( 2 2 ) cos ( 2 = + = − + + x A v t x y A v t 反射波在 x = 0 处有半波损失,令 )] 2 (2 2 2 cos ( 2 2 ) cos [ 2 = − − = − − + x A v t x y A v t 合成驻波方程为: ) 2 ) cos(2 2 1 2 2 cos(2 = + = + v t − x y y y A 或者:将 1 y 写成 ), 2 2 2 1 1 cos ( 2 2 / ) cos( 2 = + = + + − x y A t x A v t 反射波为: )] 2 (2 2 2 cos ( 2 2 ) cos [ 2 = − + = + − − x A v t x y A v t 合成驻波方程为: ) 2 ) cos(2 2 1 2 2 cos(2 = + = − v t + x y y y A
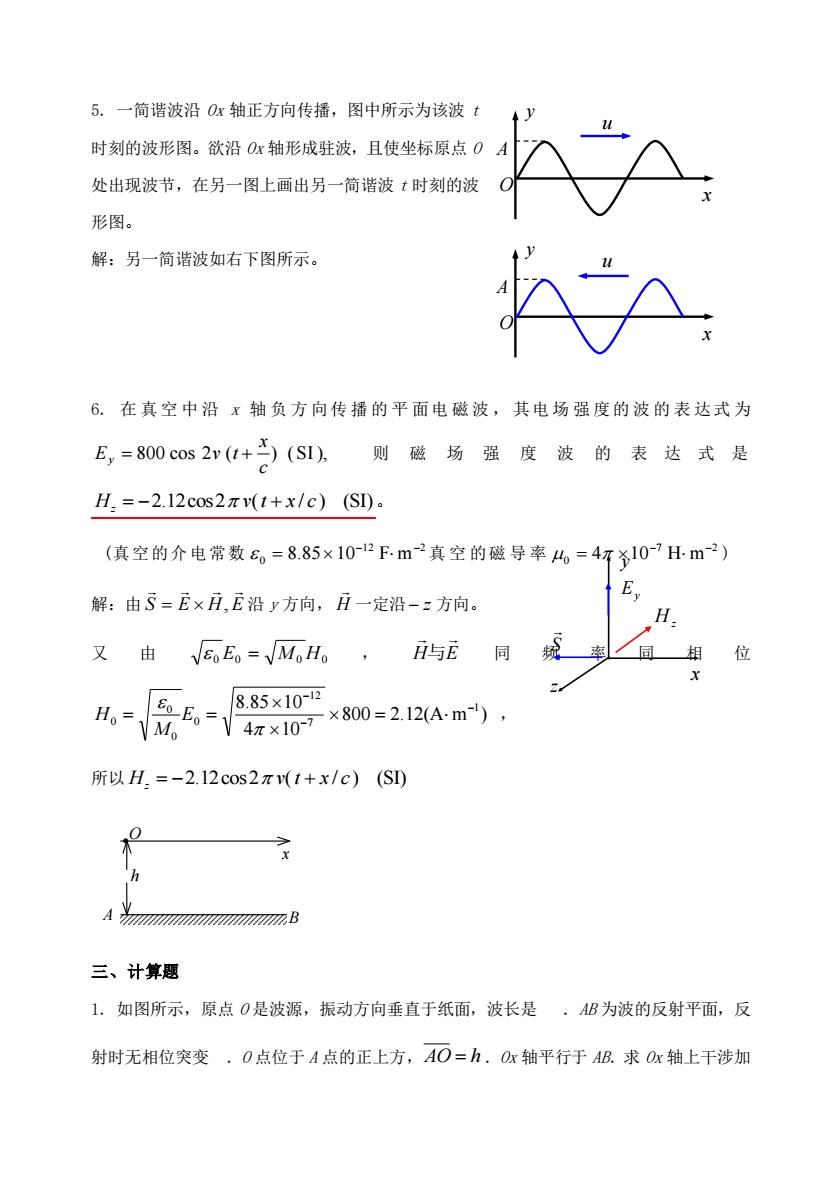
5.一简谐波沿0x轴正方向传播,图中所示为该波时刻的波形图。欲沿0x轴形成驻波,且使坐标原点0处出现波节,在另一图上画出另一简谐波t时刻的波形图。解:另一简谐波如右下图所示。6.在真空中沿轴负方向传播的平面电磁波,其电场强度的波的表达式为E, =800 cos 2v(t+) (SI),则磁场强度波的表达式是H, =-2.12cos2元v(t+x/c) (SI)。(真空的介电常数8=8.85×10-12F-m-真空的磁导率g=4π×10-7Hm2)E解:由S-ExH,E沿y方向,H一定沿-方向。H布由VEE=M.H.H与E同位又 8.85×10-260Ho=Mo×800=2.12(A·m)LE。=4元×10-7所以 H,=-2.12cos2元v(t+x/c) (SI)三、计算题1.如图所示,原点0是波源,振动方向垂直于纸面,波长是:AB为波的反射平面,反射时无相位突变:0点位于A点的正上方,AO=h。Ox轴平行于AB.求Ox轴上干涉加
5. 一简谐波沿 Ox 轴正方向传播,图中所示为该波 t 时刻的波形图。欲沿 Ox 轴形成驻波,且使坐标原点 O 处出现波节,在另一图上画出另一简谐波 t 时刻的波 形图。 解:另一简谐波如右下图所示。 6. 在真空中沿 x 轴 负 方 向传 播 的 平 面电 磁 波 , 其电 场 强 度的 波 的 表 达式 为 800 cos 2 ( ) (SI), c x E v t y = + 则 磁 场 强 度 波 的 表达式是 H 2.12cos2 v(t x / c ) (SI) z = − + 。 (真空的介电常数 12 2 0 8.85 10 F m − − = 真 空 的磁 导 率 7 2 0 4 10 H m − − = ) 解:由 S E H E = , 沿 y 方向, H 一定沿 − z 方向。 又 由 0 E0 = M0 H0 , H E 与 同频率同相位 800 2.12(A m ) 4 10 8.85 10 1 7 12 0 0 0 0 − − − = = = E M H , 所以 H 2.12cos2 v(t x / c ) (SI) z = − + x O h A B 三、计算题 1. 如图所示,原点 O 是波源,振动方向垂直于纸面,波长是 .AB 为波的反射平面,反 射时无相位突变 .O 点位于 A 点的正上方, AO = h .Ox 轴平行于 AB.求 Ox 轴上干涉加 O x y A u O x y A u S Ey H z z y x