《大学物理》作业No.1机械振动一、选择题1.一质点作简谐振动,其运动速度与时间的关系曲线如图所示。若质点的振动规律用余弦函数描述,则其初相应为:【C]-(C) _5m(B) 5元a(E) _21(0)-%解:若振动方程为x=Acos(0t+p),则速度方程为:V-Ao sin(0t+p)=+vm.cos(ot+#+)可见速度相位比位移相位超前号。由图可知速度的初相为一号,则位移的初相9=号一号=一元62.如图所示,一质量为m的滑块,两边分别与劲度系数为k和k的轻弹簧联接,两弹簧的另外两端分别固定在墙上。滑块m可在光滑的水平面上滑动,0点为系统平衡位置。现将滑块m向左移动,自静止释放,并从释放时开始m计时。取坐标如图所示,则其振动方程为:【]0Xo[[k,+k2](A) x=)XoCOVmk,k,k, +(B) x= xo cos),(C) x=Xo co+m(k +k,)[k+21+元[ki+k?(D) x= Xo cos(E) x=xo cosm解:滑块初位移为-x,初速度为0,则振幅A=-x)+(-)=xo,初相=元。设滑块处在平衡位置时,劲度系数分别为h和k的两个弹簧分别伸长A和A,则有kAx,=k,Arz,当滑块位移为x时,滑块受到合力
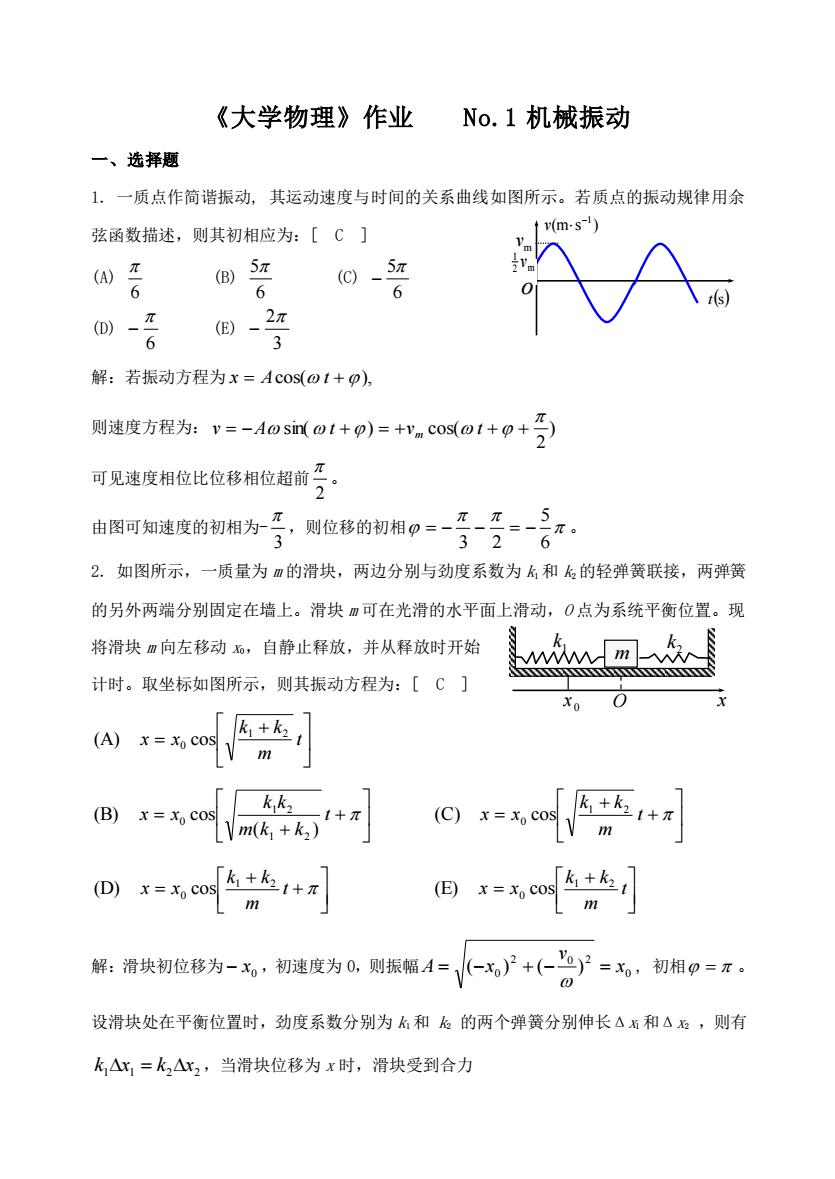
《大学物理》作业 No.1 机械振动 一、选择题 1. 一质点作简谐振动, 其运动速度与时间的关系曲线如图所示。若质点的振动规律用余 弦函数描述,则其初相应为:[ C ] (A) 6 (B) 6 5 (C) 6 5 − (D) 6 − (E) 3 2 − 解:若振动方程为 x = Acos( t +), 则速度方程为: ) 2 sin( ) cos( v = −A t + = +vm t + + 可见速度相位比位移相位超前 2 。 由图可知速度的初相为- 3 ,则位移的初相 6 5 3 2 = − − = − 。 2. 如图所示,一质量为 m 的滑块,两边分别与劲度系数为 k1 和 k2 的轻弹簧联接,两弹簧 的另外两端分别固定在墙上。滑块 m 可在光滑的水平面上滑动,O 点为系统平衡位置。现 将滑块 m 向左移动 x0,自静止释放,并从释放时开始 计时。取坐标如图所示,则其振动方程为:[ C ] + = t m k k x x 1 2 0 (A) cos + + = t m k k k k x x ( ) (B) cos 1 2 1 2 0 + + = t m k k x x 1 2 0 (C) cos + + = t m k k x x 1 2 0 (D) cos + = t m k k x x 1 2 0 (E) cos 解:滑块初位移为 0 − x ,初速度为 0,则振幅 0 2 0 2 0 ( ) ( ) x v A = −x + − = , 初相 = 。 设滑块处在平衡位置时,劲度系数分别为 k1 和 k2 的两个弹簧分别伸长Δx1 和Δx2 ,则有 1 1 2 2 k x = k x ,当滑块位移为 x 时,滑块受到合力 t(s) (m s ) −1 v m v 2 m 1 v o m x 0 x O 1 k 2 k
k,+kF=-k;(Ax +x)+k,(Ar, -x)=-(k, +k,)x=-kx 角频率 0m(+k2k+元)所以振动方程为:x=Acos(ot+p)=x.cosm3.一质点在x轴上作简谐振动,振幅A=4cm,周期T=2s,其平衡位置取作坐标原点若t=0时刻质点第一次通过x=-2cm处,且向x轴负方向运动,则质点第二次通过x-2cm处的时刻为:【B](B) s:(C) 4s(A) 1s :(D) 2s.解:由旋转失量图可知,两次通过x=-2cm所用时间为亏所以第二次通过 t=-2cm处时刻为1=1x2=2 (s)4.已知一质点沿y轴作简谐振动,其振动方程为y=Acos(ot+3元/4)。与其对应的振动曲线是:【B]MW(D)(C)11解:1Asin(odx(二元)<0故选Bt=时,y。=Acos-Aosin4<0一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为5.-振动总能量的:[E】@1:wi:(0)10:@%:(2) 16.解:弹簧振子的总能量为E=E+E,=kA,当x=时,E,=z-E,1615所以动能为E=E-E,=1%E
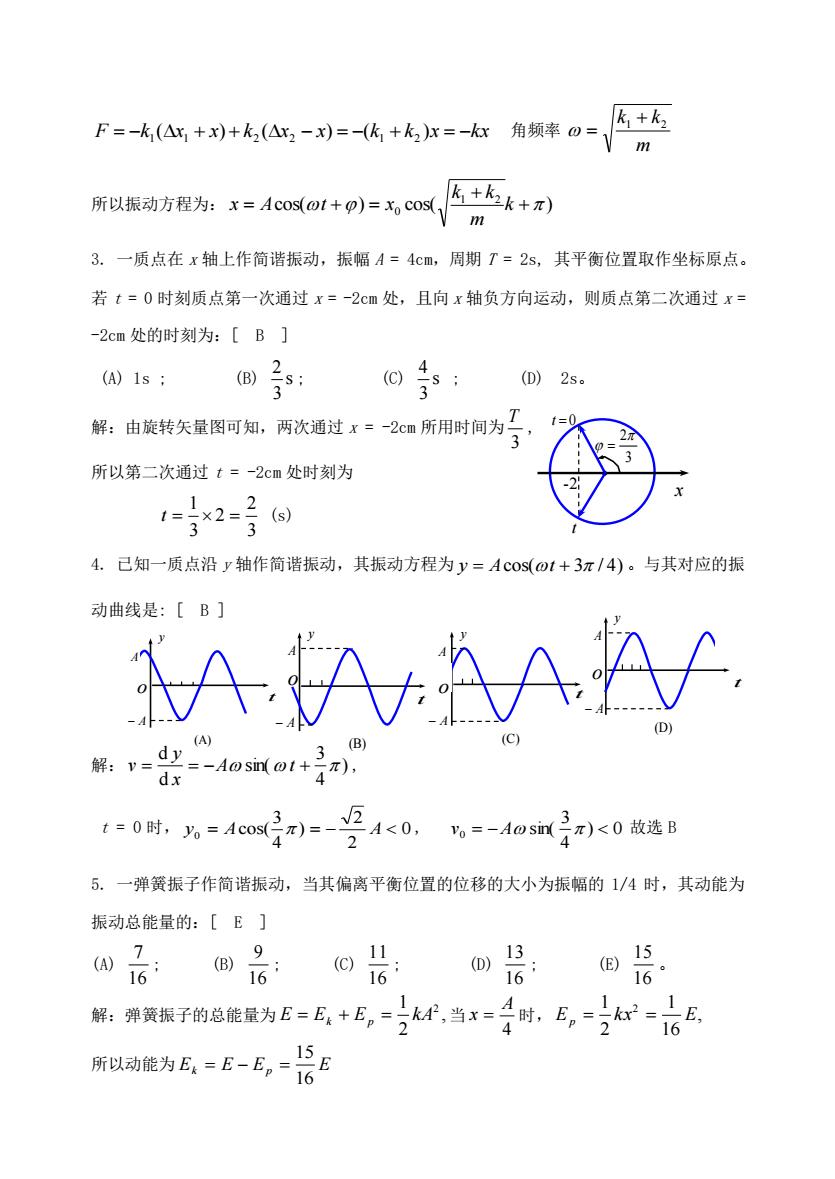
F = −k (x + x) + k (x − x) = −(k + k )x = −kx 1 1 2 2 1 2 角频率 m k k 1 + 2 = 所以振动方程为: cos( ) cos( ) 1 2 0 + + = + = k m k k x A t x 3. 一质点在 x 轴上作简谐振动,振幅 A = 4cm,周期 T = 2s, 其平衡位置取作坐标原点。 若 t = 0 时刻质点第一次通过 x = -2cm 处,且向 x 轴负方向运动,则质点第二次通过 x = -2cm 处的时刻为:[ B ] (A) 1s ; (B) s 3 2 ; (C) s 3 4 ; (D) 2s。 解:由旋转矢量图可知,两次通过 x = -2cm 所用时间为 3 T , 所以第二次通过 t = -2cm 处时刻为 3 2 2 3 1 t = = (s) 4. 已知一质点沿 y 轴作简谐振动,其振动方程为 y = Acos(t + 3 / 4) 。与其对应的振 动曲线是: [ B ] 解: ) 4 3 sin( d d = = −A t + x y v , t = 0 时, 0 2 2 ) 4 3 cos( y0 = A = − A , ) 0 4 3 sin( v0 = −A 故选 B 5. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的 1/4 时,其动能为 振动总能量的:[ E ] (A) 16 7 ; (B) 16 9 ; (C) 16 11 ; (D) 16 13 ; (E) 16 15 。 解:弹簧振子的总能量为 , 2 1 2 E = Ek + Ep = kA 当 4 A x = 时, , 16 1 2 1 2 Ep = kx = E 所以动能为 Ek E Ep E 16 15 = − = x t t = 0 -2 3 2 = t y o − A (A) A t y o A − A (B) t y A − A (C) o t y A (D) − A o
6.图中所画的是两个简谐振动的振动曲线,若这两个简谐振动可叠加,则合成的余弦振动的初相为:【B](A)1元(C)号n(B) 元(D)0A解:两个谐振动和反相,且A=2A,0A.4由矢量图可知合振动初相与x初相一致,即p=元。二、填空题1.一简谐振动的表达式为x=Acos(3t+@),已知t=0时的初位移为0.04m,初速度为0.09m-s,则振幅A=0.05m初相位=-36.90解:已知初始条件,则损幅为:4=/+=0.04 +(%)=00(m)0.09初相:=tg(-)=g"(-)=-36.9°或143.1°3×0.04ox因为>0,所以β=-36.9°2.两个弹簧振子的的周期都是0.4s,设开始时第一个振子从平衡位置向负方向运动,经过0.5s后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为元10解:从旋转矢量图可见,t= 0.05s时,A与A,反相,1=05 4/130.5即相位差为元。3.一物块悬挂在弹簧下方作简谐振动,当这物块的位移等于振幅的二率时,其动能是总能量的3/4(设平衡位置处势能为零)。当这物块在平衡位置时,弹簧的长度比原长长N,这一振动系统的周期为2元/△1/g解:谐振动总能量E=E,+E,=k4,当x=A时E=-(-
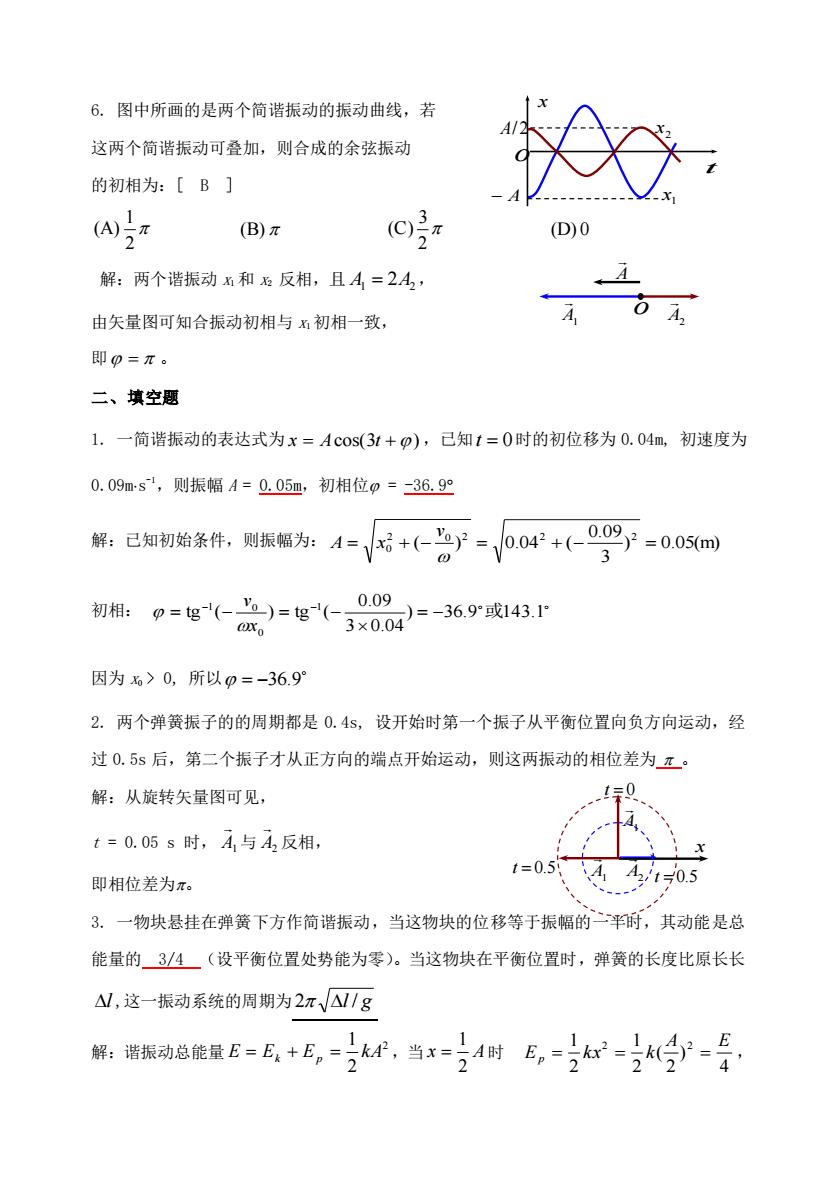
6. 图中所画的是两个简谐振动的振动曲线,若 这两个简谐振动可叠加,则合成的余弦振动 的初相为:[ B ] 2 1 (A) (B) 2 3 (C) (D) 0 解:两个谐振动 x1 和 x2 反相,且 A1 = 2A2, 由矢量图可知合振动初相与 x1 初相一致, 即 = 。 二、填空题 1. 一简谐振动的表达式为 x = Acos(3t +) ,已知 t = 0 时的初位移为 0.04m, 初速度为 0.09ms -1,则振幅 A = 0.05m,初相位 = -36.9 解:已知初始条件,则振幅为: ) 0.05(m) 3 0.09 ( ) 0.04 ( 2 0 2 2 2 = 0 + − = + − = v A x 初相: ) 36.9 143.1 3 0.04 0.09 tg ( ) tg ( 1 0 1 0 = − 或 = − = − − − x v 因为 x0 > 0, 所以 = −36.9 2. 两个弹簧振子的的周期都是 0.4s, 设开始时第一个振子从平衡位置向负方向运动,经 过 0.5s 后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为 。 解:从旋转矢量图可见, t = 0.05 s 时, A1 与 A2 反相, 即相位差为。 3. 一物块悬挂在弹簧下方作简谐振动,当这物块的位移等于振幅的一半时,其动能是总 能量的 3/4 (设平衡位置处势能为零)。当这物块在平衡位置时,弹簧的长度比原长长 l ,这一振动系统的周期为 2 l / g 解:谐振动总能量 2 2 1 E = Ek + Ep = kA ,当 x A 2 1 = 时 4 ) 2 ( 2 1 2 1 2 A 2 E E kx k p = = = , t x o A/ 2 − A 2 x 1 x o A1 A2 A A1 A1 A2 x t = 0 t = 0.5 t = 0.5

所以动能E,=E-FA物块在平衡位置时,弹簧伸长AI,则mg=k△I,k=Am=2元振动周期T=2元Vg4.上面放有物体的平台,以每秒5周的频率沿竖直方向作简谐振动,若平台振幅超过1.0×10-m,物体将会脱离平台(设g=9.8ms2)。解:在平台最高点时,若加速度大于g,则物体会脱离平台,由最大加速度a.="A=(2m)A=g得最大振幅为9.8=9.93×10-~ 1.0×10-2(m)A=:4元2/2=4元2×525.一水平弹簧简谐振子的振动曲线如图所示,振子处在位移零、速度为-のA、加速度为零和弹性力为零的状态,对应-A于曲线上的b,f点。振子处在位移的绝对值为A、速度为零、加速度为-A和弹性力-kA的状态,对应于曲线的a,点。解:位移×=0,速度v=dX=-04<0,对应于曲线上的dtb、f点;若|x=A,α=-の"A,又a=-°x,所以x=A,对应于曲线上的a、e点6.两个同方向同频率的简谐振动,其振动表达式分别为:x=6×10~cos(5t+)(SI)和X2=2×10-sin(元-5t)(SI)A它们的合振动的振幅为4×10-(m),初相位为2元解:将x改写成余弦函数形式:OAX, =2x10~ sin(π-51)=2×10-~ cos(5t-)由失量图可知,x和x反相,合成振动的振幅
所以动能 Ek E Ep E 4 3 = − = 。 物块在平衡位置时, 弹簧伸长 l ,则 mg = kl , l mg k = , 振动周期 g l k m T = 2 = 2 4. 上面放有物体的平台,以每秒 5 周的频率沿竖直方向作简谐振动,若平台振幅超过 1.0 10 m −2 ,物体将会脱离平台(设 2 9.8m s − g = )。 解:在平台最高点时,若加速度大于 g,则物体会脱离平台,由最大加速度 am = A = v A = g 2 2 (2 ) 得最大振幅为 9.93 10 1.0 10 (m) 4 5 9.8 4 3 2 2 2 2 2 − − = = = v g A 5. 一水平弹簧简谐振子的振动曲线如图所示,振子处在位移 零、速度为 − A 、加速度为零和弹性力为零的状态,对应 于曲线上的 b , f 点。振子处在位移的绝对值为 A、速度 为零、加速度为- 2 A 和弹性力-kA 的状态,对应于曲线的 a ,e 点。 解:位移 x = 0 ,速度 0 d d = = − A t x v ,对应于曲线上的 b、f 点;若|x|=A, a A 2 = − ,又 a x 2 = − , 所以 x = A,对应于曲线上的 a、e 点。 6. 两个同方向同频率的简谐振动,其振动表达式分别为: ) 2 1 6 10 cos(5 2 1 = + − x t (SI) 和 2 10 sin( 5 ) 2 2 x = − t − (SI) 它们的合振动的振幅为 4 10 (m) −2 ,初相位为 2 1 。 解:将 x2 改写成余弦函数形式: ) 2 2 10 sin( 5 ) 2 10 cos(5 2 2 2 = − = − − − x t t 由矢量图可知,x1 和 x2 反相,合成振动的振幅 t x 0 A − A a b c d e f O x A A2 1 A1

A=A -A, =6×10-2-2×10-=4×10~(m),初相g=Qi=号三、计算题1.一质量m=0.25kg的物体,在弹簧的力作用下沿x轴运动,平衡位置在原点。弹簧的劲度系数k=25N·ml(1)求振动的周期T和角频率(2)如果振幅A=15cm,t=0时物体位于x=7.5cm处,且物体沿x轴反向运动,求初速%及初相(3)写出振动的数值表达式。1分解: (1)0=/k/m=10s-l1分T=2元/0=0.63 s(2)A=15 cm在 t=0时,品= 7.5 cm,V。<0由A= /x+(u. /0)得Vo =-0/A -x --1.3 m/s2分0=tg(-v:/ox0)-1元 或 4 /32分0=↓n:%>0,(3) ×=15×10- cos(10+元)(SI)2分Vo= -0 /A -x =-10/0.152 -0.075 = -1.30(m s)(3)振动方程为x=Acos(ot+ 0)=15×10-cos(101+)(SI)2.在一平板上放一质量为m=2kg 的物体,平板在竖直方向作简谐振动,其振动周期为 Ts,振幅A=4cm,求(1)物体对平板的压力的表达式.(2)平板以多大的振幅振动时,物体才能离开平板?
6 10 2 10 4 10 (m) 2 2 2 1 2 − − − A = A − A = − = ,初相 2 1 = = 三、计算题 1. 一质量 m = 0.25 kg 的物体,在弹簧的力作用下沿 x 轴运动,平衡位置在原点. 弹簧 的劲度系数 k = 25 N·m -1. (1) 求振动的周期 T 和角频率 . (2) 如果振幅 A =15 cm,t = 0 时物体位于 x = 7.5 cm 处,且物体沿 x 轴反向运动,求 初速 v0 及初相 . (3) 写出振动的数值表达式. 解:(1) 1 / 10 s − = k m = 1 分 T = 2/ = 0.63 s 1 分 (2) A = 15 cm,在 t = 0 时,x0 = 7.5 cm,v 0 < 0 由 2 0 2 0 A = x + (v /) 得 1.3 2 0 2 v0 = − A − x = − m/s 2 分 = − = − 3 1 tg ( / ) 0 0 1 v x 或 4 /3 2 分 ∵ x0 > 0 ,∴ = 3 1 (3) ) 3 1 15 10 cos(10 2 = + − x t (SI) 2 分 10 0.15 0.075 1.30(m s ) 2 2 2 1 0 2 0 − v = − A − x = − − = − (3) 振动方程为 ) 3 cos( ) 15 10 cos(10 2 = + = + − x A t t (SI) 2. 在一平板上放一质量为 m =2 kg 的物体,平板在竖直方向作简谐振动,其振动周期为 T = 2 1 s,振幅 A = 4 cm,求 (1) 物体对平板的压力的表达式. (2) 平板以多大的振幅振动时,物体才能离开平板?