
《大学物理》作业No.2波动方程一、选择题1.一平面简谐波表达式为y=-0.05sin 元(t-2x)(SI),则该波的频率(Hz)、波速u(ms")及波线上各点振动的振幅A(m)依次为:[C](A)1/2,1/2,-0.05(B)1/2,1,-0.05(C)1/2,1/2,0.05(D)2,2,0.05解:平面简谐波表达式可改写为y=-0.05sin (t-2x)= 0.05cos(πt-2x +) (SI)与标准形式的波动方程y=Acos[2m(t-)+]比较,可得A= 0.05 (m) ,V=(H2),u=_ (m.s-")。故选C2.一横波沿绳子传播时的波动方程为y=0.05cos(4元x-10元t)(SI),则【A】(B)波速为 5 ms ;(A)其波长为0.5㎡;(D)频率 2 Hz 。(C)波速25ms;解:将波动方程与标准形式y=Acos[2m(t-)+p]比较,可知α=兰-=0.5(m)放述Av=5(Hz), u=2.5(ms)3.一平面简谐波的波动方程为y=0.1cos(3元t-元x+元)(SI),t=0时的波形曲线如图所示。则[]Y(m)(A)0点的振幅为-0.1m:0.1(B)波长为3 m;X(m)(C)a、b两点位相差元;(D) 波速为 9 m-sl。解:由波动方程可知A=0.1(m),V=号(H2),几=2(m),u=Va=号x2=3(m-s")
《大学物理》作业 No.2 波动方程 一、选择题 1. 一平面简谐波表达式为 y = −0.05sin (t − 2x) (SI) ,则该波的频率 v (Hz)、波速 u(ms -1 )及波线上各点振动的振幅 A(m)依次为: [ C ] (A) 1/ 2,1/ 2 , − 0.05 (B) 1/ 2 ,1, − 0.05 (C) 1/ 2 ,1/ 2 , 0.05 (D) 2 ,2 ,0.05 解:平面简谐波表达式可改写为 ) (SI) 2 0.05sin ( 2 ) 0.05cos( 2 y = − t − x = t − x + 与标准形式的波动方程 = cos[ 2 ( − ) + ] u x y A v t 比较,可得 (m s ) 2 1 (Hz) , 2 1 0.05 (m) , −1 A = v = u = 。 故选 C 2. 一横波沿绳子传播时的波动方程为 y = 0.05cos(4 x −10 t) (SI),则 [ A ] (A) 其波长为 0.5 m ; (B) 波速为 5 ms -1 ; (C) 波速 25 ms -1 ; (D) 频率 2 Hz 。 解:将波动方程与标准形式 = cos[ 2 ( − ) + ] u x y A v t 比较,可知 5( Hz ), 2.5(m s ) −1 v = u = 0.5 ( m ) 5 2.5 = = = v u 故选 A 3. 一平面简谐波的波动方程为 y = 0.1 cos(3 t − x + ) (SI),t = 0 时的波形曲线如 图所示。则[ C ] (A) O 点的振幅为−0.1 m; (B) 波长为 3 m; (C) a 、b 两点位相差 2 1 ; (D) 波速为 9 ms -1。 解:由波动方程可知 (Hz), 2 3 A = 0.1(m), = = 2(m) , 2 3(m s ) 2 3 −1 u = = = Y(m) u 0.1 a b X (m) 0 −0.1

ah2元/4故选Ca、b两点间相位差为:△p=214.一简谐波沿x轴负方向传播,圆频率为の,波速为u。设t=T/4时刻的波形如图所示,则该波的表达式为:[D](A) y= Acoso(t -x / u)(B) y= Acos[o(t-x / )+(C) y= Acos[o(t+ x / u)(D) y= Acos[o(t+x/u)+ π)解:由波形图向右科元,可得t=0时波形如图中虚线所示。在0点,t=0时y=-A,初相Φ=元,振动方程为y。=Acos(のt+元)。又因波向(-x)方向传播,所以波动方程为y= Acos[0(++)+m](SI)故选D5.一平面简谐波沿×轴正向传播,t=T/4时的波形曲线如图所示。若振动以余弦函数表示,且此题各点振动的初相取一元到元之间的值,则[D](A)0点的初位相为=0(B)1点的初位相为=-(C)2点的初位相为,=元(D)3点的初位相为9;=一号解:波形图左移入/4,即可得t=0时的波形图,由t=0的波形图(虚线)可知,各点的L振动初相为:=0=元,01-号:02=0,03=-号故选DX2
a 、b 两点间相位差为: 2 4 2 2 = = = ab 故选 C 4. 一简谐波沿 x 轴负方向传播,圆频率为 ,波速为 u。设 t = T /4 时刻的波形如图所 示,则该波的表达式为: [ D ] (A) y = Acos(t − x / u) ] 2 (B) cos[ ( / ) y = A t − x u + (C) y = Acos[(t + x / u)] (D) y = Acos[(t + x / u) + ] 解:由波形图向右移 4 1 ,可得 t = 0 时波形如图中虚线所示。在 0 点, t = 0 时 y = -A, 初 相 = , 振动方程为 cos( ) y0 = A t + 。又因波向 (−x) 方 向传播,所以波动方程为 = cos[ ( + ) + ] (SI) u x y A t 故选 D 5. 一平面简谐波沿 x 轴正向传播,t = T/4 时的波形曲线如图所示。若振动以余弦函数 表示,且此题各点振动的初相取 − 到 之间的值,则[ D ] (A) 0 点的初位相为 0 = 0 (B) 1 点的初位相为 2 1 = − (C) 2 点的初位相为 2 = (D) 3 点的初位相为 2 3 = − 解:波形图左移 / 4 ,即可得 t = 0 时的波形图,由 t = 0 的波形图(虚线)可知,各点的 振动初相为: 2 , 0 , 2 , 0 1 2 3 = = = = − 故选 D y u 1 x 0 2 3 4 y u 1 x 0 2 3 4 t = 0 y u A x 0 − A y u A x 0 − A t = 0

二、填空题1.已知一平面简谐波沿x轴正向传播,振动周期T=0.5s,波长入=10m,振幅A=0.1m当t=0时波源振动的位移恰好为正的最大值。若波源处为原点,则沿波传播方向距离波源为入/2处的振动方程为y=0.1cos(4元t-元)(SI)。当t=T/2时,x=/4处质点的振动速度为-1.26ms-l。解: 波动方程为y=Acos2 (六-著-)=0.1cos[2元(2t-0.1x) (SD),x==5m处的质点振动方程为y=0.1cos(4元t-元)(SI)=2.5m处的振动方程为y=0.1cos(4元t-)=0.1si(4元l)=0.1×4元cos(4元l)=0.4元 cos(4元l)振动速度V=dtt==0.25s 时V=0.4元cos(4元×0.25)=-0.4元=-1.26(m-s)2.如图所示为一平面简谐波在t=2s时刻的波形图,该谐波的波动方程是y(m)-4002岁(-2-+型 P处质点的报 二Px(m动方程是y,=Acos[2元(t-2)-]。(该波的振幅A、波速u与波长为已知量)解:由t=2s波形图可知,原点0的振动方程为=Acos[2m(t-2)+=Acos[2m(-2)+波向+x方向传播,所以波动方程为y=Acos[2(-2-)+】(SI)P点x=二,振动方程为y=Acos[2元(-2)+=Acos2元(2)3.一简谐波沿x轴正向传播。x,和xz两点处的振动曲线分别如图(a)和(b)所示。已
二、填空题 1. 已知一平面简谐波沿 x 轴正向传播,振动周期 T = 0.5 s,波长 = 10m , 振幅 A = 0.1m。 当 t = 0 时波源振动的位移恰好为正的最大值。若波源处为原点,则沿波传播方向距离波 源为 / 2 处的振动方程为 y = 0.1 cos (4 t − ) (SI) 。当 t = T / 2 时, x = / 4 处 质点的振动速度为 1 1.26m s − − 。 解:波动方程为 cos[2 ( )] 0.1cos[2 (2t 0.1x) (SI) x T t y = A − = − , 5m 2 = = x 处的质点振动方程为 y = 0.1cos(4 t − ) (SI) 2.5m 4 = = x 处的振动方程为 ) 0.1sin( 4 ) 2 y 0.1cos(4 t t = − = 振动速度 0.1 4 cos(4 ) 0.4 cos(4 ) d d t t t y v = = = 0.25s 2 = = T t 时 0.4 cos(4 0.25) 0.4 1.26(m s ) −1 v = = − = − 2. 如图所示为一平面简谐波在 t = 2s 时刻的波形图,该谐波的波动方程是 ] 2 cos[2 ( 2 ) = − − + u x t u y A ;P 处质点的振 动方程是 ] 2 cos[2 ( 2) = t − − u y p A 。(该波的振 幅 A、波速 u 与波长为已知量) 解:由 t = 2s 波形图可知,原点 O 的振动方程为 ] 2 cos[2 ( 2) 0 y = A v t − + ] 2 cos[2 ( 2) = t − + u A v 波向+x 方向传播,所以波动方程为 ] 2 cos[2 ( 2 ) = − − + u x t u y A v (SI) P 点 2 x = ,振动方程为 ] 2 ] cos[2 ( 2) 2 ) 2 cos[2 ( 2 = − − + = t − − u A u t u yP A 3. 一简谐波沿 x 轴正向传播。 1 x 和 2 x 两点处的振动曲线分别如图(a) 和 (b) 所示。已 y(m) u O P x(m) A
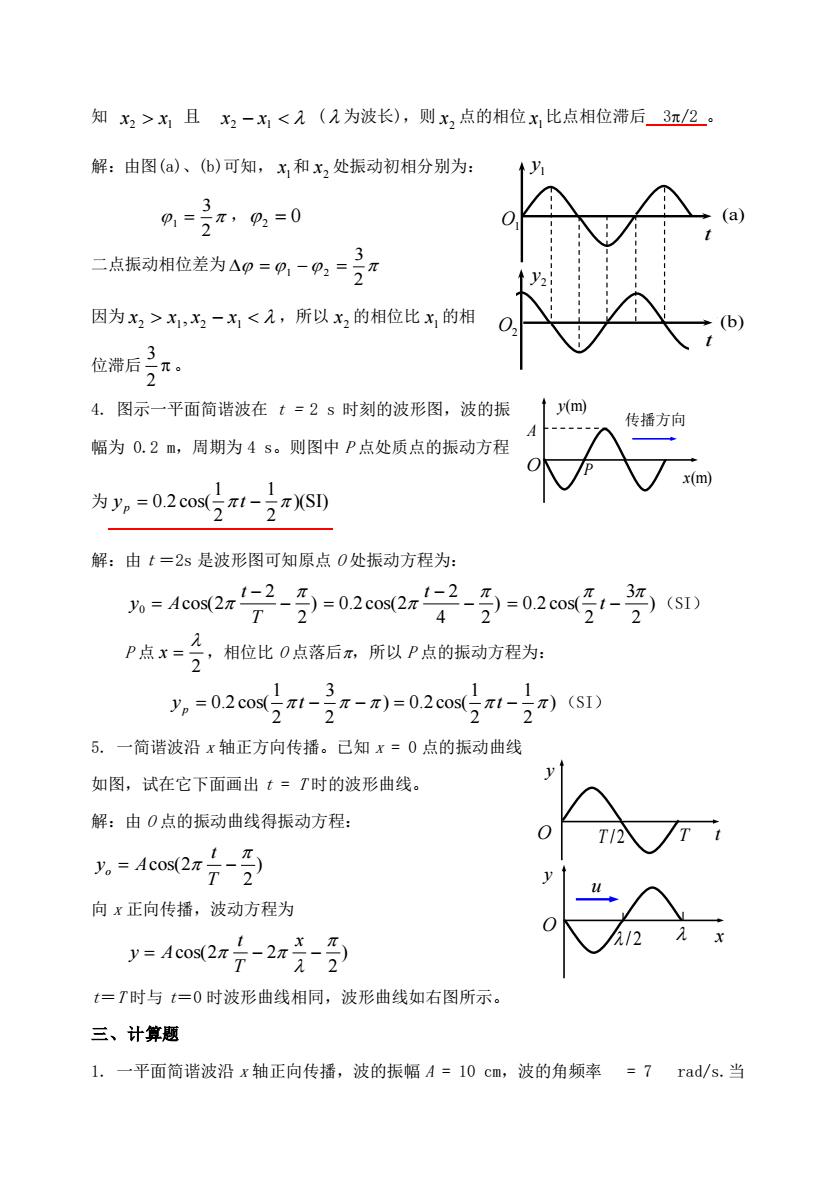
知x>x且x2-xi(为波长),则x,点的相位x,比点相位滞后_3元/2。解:由图(a)、(b)可知,x,和x,处振动初相分别为:-1=号2=0二点振动相位差为=92=号元t y2!P因为>-,所以的相位比的相6位滞后号元。4.图示一平面简谐波在t=2s时刻的波形图,波的振I y(m)传播方向幅为0.2m,周期为4s。则图中P点处质点的振动方程2x(m为y,= 0.2 cos(元t-元)(SI)解:由t=2s是波形图可知原点0处振动方程为:)=0.20o(号)(S1)y = Acos(2元2-)=0.2 cos(2元P点x=,相位比0点落后元,所以P点的振动方程为:,=0.2cos(元t-号元)=0.2cos(-元)(SI)5:一简谐波沿x轴正方向传播。已知x=0点的振动曲线y如图,试在它下面画出t=T时的波形曲线。解:由0点的振动曲线得振动方程:OTT。 = Acos(2 -)向x正向传播,波动方程为212=Aco(2 —-2 元-)t=T时与t=0时波形曲线相同,波形曲线如右图所示。三、计算题一平面简谐波沿x轴正向传播,波的振幅A=10cm,波的角频率=7rad/s.当
知 2 1 x x 且 x2 − x1 ( 为波长),则 2 x 点的相位 1 x 比点相位滞后 3/2 。 解:由图(a)、(b)可知, 1 x 和 2 x 处振动初相分别为: 2 3 1 = ,2 = 0 二点振动相位差为 2 3 = 1 − 2 = 因为 x2 x1 , x2 − x1 ,所以 2 x 的相位比 1 x 的相 位滞后 2 3 。 4. 图示一平面简谐波在 t = 2 s 时刻的波形图,波的振 幅为 0.2 m,周期为 4 s。则图中 P 点处质点的振动方程 为 )(SI) 2 1 2 1 y p = 0.2 cos( t − 解:由t=2s 是波形图可知原点 O 处振动方程为: ) 2 2 0 cos(2 − − = T t y A ) 4 2 2 0.2 cos(2 − − = t ) 2 3 2 0.2 cos( = t − (SI) P 点 2 x = ,相位比 O 点落后,所以 P 点的振动方程为: ) 2 1 2 1 ) 0.2 cos( 2 3 2 1 y p = 0.2 cos( t − − = t − (SI) 5. 一简谐波沿 x 轴正方向传播。已知 x = 0 点的振动曲线 如图,试在它下面画出 t = T 时的波形曲线。 解:由 O 点的振动曲线得振动方程: ) 2 cos(2 = − T t yo A 向 x 正向传播,波动方程为 ) 2 cos(2 2 = − − x T t y A t=T 时与 t=0 时波形曲线相同,波形曲线如右图所示。 三、计算题 1. 一平面简谐波沿 x 轴正向传播,波的振幅 A = 10 cm,波的角频率 = 7 rad/s.当 1 y t O1 (a) 2 y O2 t (b) P y(m) A O 传播方向x(m) u O T / 2 y T t O / 2 y x

t=1.0s时,x=10cm处的a质点正通过其平衡位置向y轴负方向运动,而x=20cm处的b质点正通过y=5.0cm点向y轴正方向运动。设该波波长>10cm,求该平面波的表达式.解:设平面简谐波的波长为,坐标原点处质点振动初相为,则该列平面简谐波的表达2 分式可写成y=0.1cos(7元t-2元x/ a+) (SI)t=1 s时y= 0.1cos[7元 -2元(0.1/ 2)+]=0因此时a质点向y轴负方向运动,故①2分7元-2元(0.1/2)+0=元而此时,b质点正通过y=0.05m处向y轴正方向运动,应有y= 0. 1cos[7元-2元(0.2 / 2)+] = 0.05且7元-2元(0.2 / 2)+=-?2分= 0. 24 m1分由①、②两式联立得Φ=-17元/31分:、该平面简谐波的表达式为17y = 0. 1cos[7元t -元) (SI)2分0.123或y=0. 1cos[7nt-01 +3元](SI)2.一平面简谐波沿x轴正向传播,其振幅为A,频率为,波速为u.设t=t时刻的波形曲线如图所示。求(1)x=0处质点振动方程;(2)该波的表达式
t = 1.0 s 时,x = 10 cm 处的 a 质点正通过其平衡位置向 y 轴负方向运动,而 x = 20 cm 处的 b 质点正通过 y = 5.0 cm 点向 y 轴正方向运动.设该波波长 >10 cm,求该平面波 的表达式. 解:设平面简谐波的波长为 ,坐标原点处质点振动初相为 ,则该列平面简谐波的表达 式可写成 y = 0.1cos(7t − 2x / +) (SI) 2 分 t = 1 s 时 y = 0.1cos[7 − 2(0.1/ ) +] = 0 因此时 a 质点向 y 轴负方向运动,故 − + = 2 1 7 2 (0.1/ ) ① 2 分 而此时,b 质点正通过 y = 0.05 m 处向 y 轴正方向运动,应有 y = 0.1cos[7 − 2(0.2 / ) +] = 0.05 且 − + = − 3 1 7 2 (0.2 / ) ② 2 分 由①、②两式联立得 = 0.24 m 1 分 = −17/ 3 1 分 ∴ 该平面简谐波的表达式为 ] 3 17 0.12 0.1cos[7 − = − x y t (SI) 2 分 或 ] 3 1 0.12 0.1cos[7 + = − x y t (SI) x u O t=t′ y 2. 一平面简谐波沿 x 轴正向传播,其振幅为 A,频率为 ,波速为 u.设 t = t'时刻的 波形曲线如图所示.求 (1) x = 0 处质点振动方程; (2) 该波的表达式.