《大学物理学》课程作业习题（含解答）No.7-1 电场强度

《大学物理AI》作业No.6电场强度一、选择题：（注意：题目中可能有一个或几个正确答案）1.真空中一“无限大”均匀带负电荷的平面如图所示，其电场的场强分布图线应是（设场强方向向右为正、向左为负）【D］EEL6/2600720(A)x(B)E1s1260-8/260(C)(D)8/2818/260解：均匀带负电的“无限大”平板两侧为均匀电场，场强方向垂直指向带负电平板，即X0时，E<0：x>0时，E>0故选D2.两个同心均匀带电球面，半径分别为R和R（R。<R），所带电量分别为和Q，设某点与球心相距r，当R<r《R时，该点的电场强度的大小为：【D］(A).+O)1..-0（B）4元%4元起1.0(c)(D）4元起724元%解：作半径为r的同心球面为高斯面，由高斯定理f,E·ds=4r*E=0Qa得该点场强大小为：E=4元6or故选D3.如图所示，两个“无限长”的、半径分别为R和R的共轴圆柱面均带电，轴线方向单位长度上的带电量分别为入，和入。，则在内圆柱面里面、距离轴线为r处的P点的电场强度大小［D］(A)3+2元元(B)2元60r2元80R*2元60R2

2 0  /  E o x 2 0  /  E o x 2 0  /  2 0 − /  E o x 2 0  /  2 0 − /  o E x 《大学物理 AI》作业 No.6 电场强度 一、选择题：（注意：题目中可能有一个或几个正确答案） 1．真空中一“无限大”均匀带负电荷的平面如图所示，其电场的场强分布 图线应是（设场强方向向右为正、向左为负）[ D ] （A） （B） （C） （D） 解：均匀带负电的“无限大”平板两侧为均匀电场，场强方向垂直指向带负电平板， 即 x<0 时，Ex<0；x>0 时，Ex>0。 故选 D 2．两个同心均匀带电球面，半径分别为 Ra 和 Rb ( Ra <Rb ) ,所带电量分别为 Qa 和 Qb， 设某点与球心相距 r, 当 Ra < r < Rb 时， 该点的电场强度的大小为：[ D ] ( A ) 2 4 0 1 r Qa + Qb   ( B ) 2 4 0 1 r Qa − Qb   ( C ) ( ) 4 1 2 2 0 b a b R Q r Q  +  ( D ) 2 4 0 1 r Qa   解：作半径为 r 的同心球面为高斯面，由高斯定理 0 2 d 4   a S Q E  S = r E =    。 得该点场强大小为： 2 4 0 r Q E a  = 。 故选 D 3. 如图所示，两个“无限长”的、半径分别为 R1 和 R 2 的共轴圆柱面均匀 带电，轴线方向单位长度上的带电量分别为λ1 和λ2 ， 则在内圆柱面里面、 距离轴线为 r 处的 P 点的电场强度大小[ D ] ( A ) r0 1 2 2  +  ( B ) 0 2 2 0 1 1 2 R 2 R    + − x o 1 2 R1 R2 r O P

2(c)(D) 04元60R解：过P点作如图同轴高斯面S，由高斯定理fE·dS=2元rlE=0，所以 E=0。故选D4有两个点电荷电量都是+g，相距为2a，今以左边的点电荷所在处为球心，以a为半径作一球形高斯面，在球a2g面上取两块相等的小面积S和S2，其位置如图所示，设通过S和S，的电场强度分别为Φ，和Φ2，通过整个球面的电场强度通量为Φ，则［D](A)>2,Φ,=q /e。(B) Φi<@2, @,=24 /eo(D) 0r<02, 0.=g /c.(C) Φr = Φ2 Φ,= q /eo解：由高斯定理，Φ，=q/s。在S处，E,=0，Φ,=0在S2处，E,*0，Φ,=E,-S,>0,所以Φ1<Φ2故选D5.图示为一具有球对称性分布的静电场的E~r关系曲线，请指出该静电E场是由下列那种带电体产生的。［（A）半径为R的均匀带电球面。（B）半径为R的均匀带电球体。（C）半径为R的、电荷体密度为p=Ar（A为常数）的非均匀带电球体。（D）半径为R的、电荷体密度为p=A/r（A为常数)的非均匀带电球体。解：对于球对称分布的带电体，由高斯定理可知，场强分布为E=，因此4元g半径为R的均匀带电球面KR时，E=0：半径为R的均勾带电球体，4一"p，p为电荷体密度（KM)，可知

( C ) 0 1 1 4 R  ( D ) 0 解：过 P 点作如图同轴高斯面 S，由高斯定理  d = 2 = 0  E S rlE S    ， 所以 E＝0。 故选 D 4．有两个点电荷电量都是 +q ， 相距为 2a , 今以左边的 点电荷所在处为球心， 以 a 为半径作一球形高斯面，在球 面上取两块相等的小面积 S1 和 S 2 , 其位置如图所示 ， 设通过 S1 和 S 2 的电场强度分别为 Φ1 和Φ2 ，通过整个球面的电场强度通量为Φs，则 [ D ] ( A ) Φ1 > Φ2 , Φs = q /ε0 ( B ) Φ1 < Φ2 , Φs = 2q /ε0 ( C ) Φ1 = Φ2 , Φs = q /ε0 ( D ) Φ1 < Φ2 , Φs = q /ε0 解：由高斯定理， 0 q / S = ， 在 S1 处， E1 = 0， 1 = 0 ； 在 S 2 处， E2  0，2 = E2  S2  0   ，所以 1  2 故选 D 5．图示为一具有球对称性分布的静电场的 E ~ r 关系曲线 ， 请 指出该静电 E 场是由下列那种带电体产生的。[ B ] ( A ) 半径为 R 的均匀带电球面。 ( B ) 半径为 R 的均匀带电球体。 ( C ) 半径为 R 的、电荷体密度为ρ=Ar (A 为常数)的非均匀带电球体。 ( D ) 半径为 R 的、电荷体密度为ρ=A/r (A 为常数)的非均匀带电球体。 解：对于球对称分布的带电体，由高斯定理可知，场强分布为 2 0 4 r q内 E = ，因此， 半径为 R 的均匀带电球面 r<R 时，E＝0； 半径为 R 的均匀带电球体，   3 r 3 4 q内 ＝ ，  为电荷体密度（r<R），可知 2 r 1 E  O R r E O 1 S2 S a 2a X q q

1元r'pI<R处,E=元AR'pr>R处，E4元236.r2同理可知，（C）、(D）电荷分布产生的电场强度分布与图示不符。故选B二、填空题：1.两块“无限大”的带电平行电板，其电荷面密度分别为8（8）0）及-28，如图所示试写出各区域的电场强度E。0/260-20I区E的大小方向向右0/2-g/203g/260I区E的大小方向向右2g/282g/28G/260—ⅢⅢI区E的大小，方向一向左解：两个无限大带电平板单独在两侧都产生匀强电场，场强大小和方向如图所示。由场强叠加原理，可得各区域场强大小和方向为：（设向右为正）2gI区：E，方向向右280280-2602g+03gI区：E=，方向向右2802802800区：E=+，方向向左280280260AB2.A、B为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小都为 Ec，两平面外侧电场强度大小都为E。/3EoEo方向如图。则A、B两平面上的电荷面密度分别为Eo-26gE。/34sE/3SA=OB解：设A、B两板的电荷面密度分别为8A、SB（均匀为正)，各自在两侧产生的场强大小和方向如图所示。由场强叠加原理及题设条件可知：（设向右为正）

2 2 0 2 0 3 0 2 0 3 r 1 4 3 r R 3 4 E 4 3 r 3 4 r R E  = =   = =              r r R r r r 处， 处， 同理可知，（C）、（D）电荷分布产生的电场强度分布与图示不符。 故选 B 二、填空题： 1．两块“无限大”的带电平行电板，其电荷面密度分别为δ（δ> 0）及-2δ，如图所示， 试写出各区域的电场强度 E  。 Ⅰ区 E  的大小 2 0  /  ， 方向 向右 。 Ⅱ区 E  的大小 2 0 3 /  ， 方向 向右 。 Ⅲ区 E  的大小 2 0  /  ， 方向 向左 。 解：两个无限大带电平板单独在两侧都产生匀强电场，场强大小和方向如图所示。由场强叠 加原理，可得各区域场强大小和方向为：（设向右为正） Ⅰ区： 2 0 2 0 2 0 2       E = − = ，方向向右。 Ⅱ区： 0 0 2 0 3 2 2 2       E = ＋ = ，方向向右。 Ⅲ区： 2 0 2 0 2 0 2       E =－ ＋ = − ，方向向左。 2．A、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面 间的电场强度大小都为 E0 , 两平面外侧电场强度大小都为 E0 / 3 ， 方向如图。则 A、B 两平面上的电荷面密度分别为  A = －2 0E0 /3 ， B = 4 0E0 /3 。 解：设 A、B 两板的电荷面密度分别为  A 、 B （均匀为正），各自在两侧产生的场强大小 和方向如图所示。由场强叠加原理及题设条件可知：（设向右为正） A B 3 E0 3 E0 E0 I II III  − 2 0  / 2 0  / 2 0 2 / 2 0 2 / 2

+B=E ()O260+2602600a06OB-CA=Eo(2)O2260260由上两式联解可得：III8A=—26E。/3，（负号说明与题设相反，即8A<0）g=4sgE/33.真空中一半径为R的均匀带电球面，总电量为Q（Q0）。今在理挖去非常小块的面积△S（连同电荷），且假设不影响原来的电荷分布，则△QAS /(16元*8,R*)挖去AS后球心处电场强度的大小方向为由球心 0点指向 AS解：由场强叠加原理，挖去△S后的电场可以看作由均匀带电球面和带负电的△S（面密度与球面相同）叠加而成，在球心处，均匀带电球面产生的场强为零，△S（视为点电荷）产OASOAS生的场强大小为：E4元60R216元80R4方向由球心指向△S4，有二个球形的橡皮膜气球，电荷9均匀地分布在球面上，在此气球被吹大的过程中，被q(4元8r3)气球表面掠过的点（该点与球中心距离为1)，其电场强度的大小将由为解：由高斯定理可知，均匀带电球面内部场强为零，外部任意一点场强q/（4元8r2）。在气球被吹大的过程中，被气球掠过的点都从球外变为球内，因此其场强大小由q(4元or2）变为零。三、计算题：1．一段半径为a的细圆弧，对圆心的张角为0。，其上均匀分布有正电中图所示，试以a，9，0。表示出圆心0处的电场强度。gdg-deelq.dl解：建立如图坐标系，在细圆弧上取电荷元dg=addEa电荷元视为点电荷，它在圆心处产生的场强大小为：

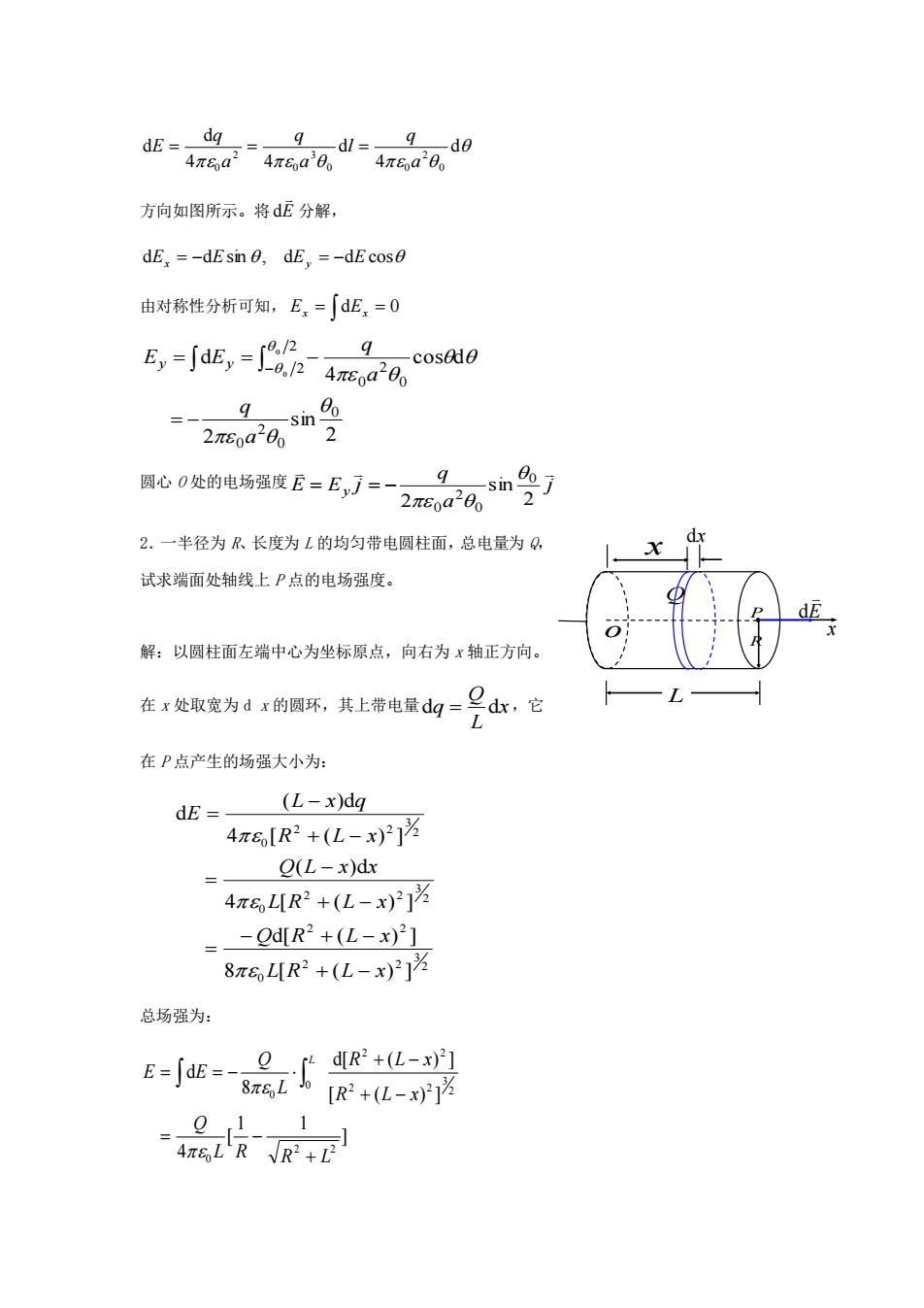
(2) 2 2 (1) 3 1 2 2 0 0 0 0 0 0 E E B A A B − = + =         由上两式联解可得：  A =－2 0E0 /3 ，（负号说明与题设相反，即  A  0 ）  B = 4 0E0 /3 3．真空中一半径为 R 的均匀带电球面，总电量为 Q（Q> 0）。今在球面上 挖去非常小块的面积ΔS（连同电荷），且假设不影响原来的电荷分布，则 挖去ΔS 后球心处电场强度的大小 E＝ /(16 ) 4 0 2 QS   R 。 其 方向为 由球心 O 点指向 S 。 解：由场强叠加原理，挖去 S 后的电场可以看作由均匀带电球面和带负电的 S （面密度 与球面相同）叠加而成，在球心处，均匀带电球面产生的场强为零， S （视为点电荷）产 生的场强大小为： 4 0 2 2 4 0 16 R S R S E       =  = ， 方向由球心指向ΔS。 4．有一个球形的橡皮膜气球，电荷 q 均匀地分布在球面上，在此气球被吹大的过程中， 被 气球表面掠过的点（该点与球中心距离为 r），其电场强度的大小将由 /(4 ) 2 0 q  r 变 为 0 。 解：由高斯定理可知，均匀带电球面内部场强为零，外部任意一点场强 /(4 ) 2 0 q  r 。在 气球被吹大的过程中，被气球掠过的点都从球外变为球内，因此其场强大小由 /(4 ) 2 0 q  r 变为零。 三、计算题： 1．一段半径为 a 的细圆弧，对圆心的张角为θ0，其上均匀分布有正电荷 q，如图所示，试 以 a, q, θ0 表示出圆心 O 处的电场强度。 解：建立如图坐标系，在细圆弧上取电荷元 l a q dq d 0 =   ， 电荷元视为点电荷，它在圆心处产生的场强大小为： O S R  0 a q o + + + + + +  E  d d y x dq dEx dEy 2 0   B 2 0   B 2 0   A 2 0   A I II III

dE164元-4元04元60a*0方向如图所示。将dE分解，dE,=-dEsin e, dE,=-dEcoso由对称性分析可知，E,=JdE,=0E, = JdE, = [0,/2cosede1-0./24元0~0000S2元80a200圆心0处的电场强度E=E,J=sin%2元602002.一半径为R长度为L的均匀带电圆柱面，总电量为0,试求端面处轴线上P点的电场强度。解：以圆柱面左端中心为坐标原点，向右为x轴正方向。在x处取宽为dx的圆环，其上带电量dgdx，它在P点产生的场强大小为：(L- x)dqgdE:4[R2 +(L-x)]Q(L -x)dx4L[R2 +(L-x)"]Qd[R? +(L -x)"]8元[R2 +(L-)]总场强为：_.L" d[R*+(L-x)]E=JdE=-8元 J。 [R*+(L-x)%Q.14元L'RVR+L

         d 4 d 4 4 d d 0 2 0 0 3 0 2 0 a q l a q a q E = = = 方向如图所示。将 E  d 分解， dEx = −dEsin  , dEy = −dE cos 由对称性分析可知，  Ex = dEx = 0 2 sin 2 cos d 4 d 0 0 2 0 2 2 0 2 0 0 0          a q a q Ey Ey = − =  =  − − 圆心 O 处的电场强度 j a q E E j y    2 sin 2 0 0 2 0    = = − 2．一半径为 R、长度为 L 的均匀带电圆柱面，总电量为 Q， 试求端面处轴线上 P 点的电场强度。 解：以圆柱面左端中心为坐标原点，向右为 x 轴正方向。 在 x 处取宽为 d x 的圆环，其上带电量 x L Q dq = d ，它 在 P 点产生的场强大小为： 2 3 2 2 0 2 2 2 3 2 2 0 2 3 2 2 0 8 [ ( ) ] d[ ( ) ] 4 [ ( ) ] ( )d 4 [ ( ) ] ( )d d L R L x Q R L x L R L x Q L x x R L x L x q E + − − + − = + − − = + − − =       总场强为： ] 1 1 [ 4 [ ( ) ] d[ ( ) ] 8 d 2 2 0 2 3 2 2 2 2 0 0 L R R L Q R L x R L x L Q E E L + = − + − + − = = −        Q L P R x E  d o dx x