5.2常用信号的拉氏变换 () ealu(t) 1 s+a t”u(t) n 1 t u(t) 6(t) 1 8(t-to)) e -sto
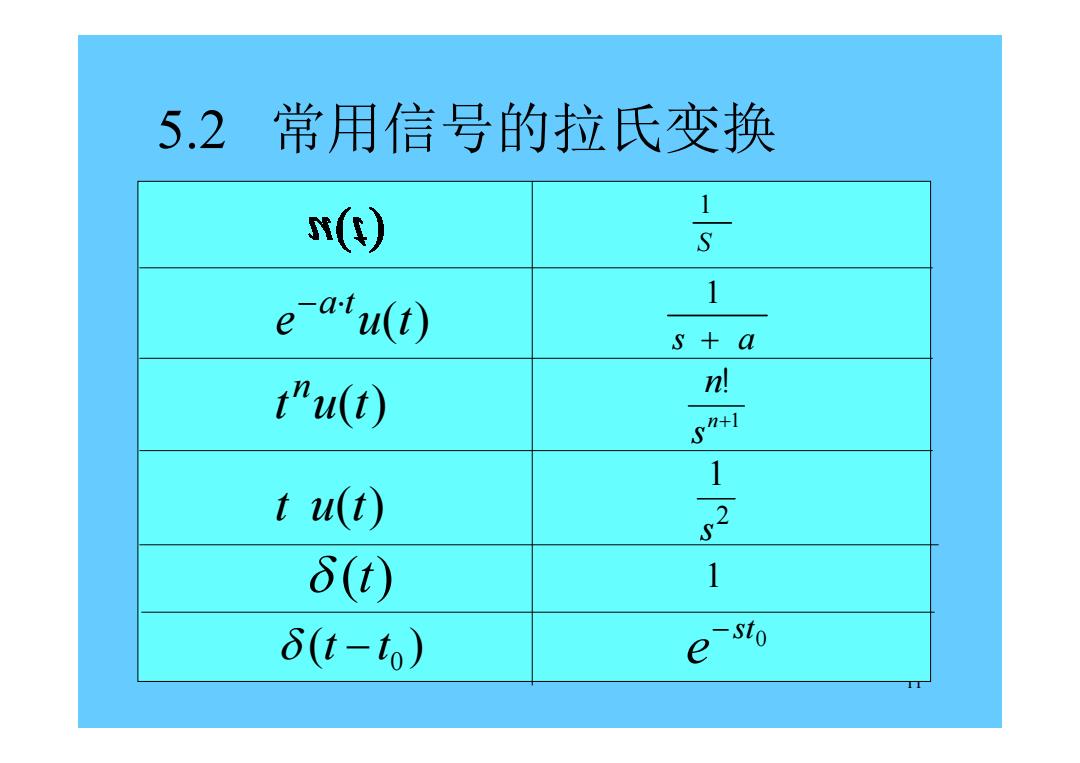
11 5.2 常用信号的拉氏变换 S 1 e u(t) at s a 1 t u(t) n 1 ! n s n (t) 1 ( )0 t t 0 st e t u(t) 2 1 s

5.3拉氏变换的基本性质(1) n n 线性 f0 ∑k,LTIf() i= H 时移 f(t-to)u(t-to) e-stoF(s) 尺度变换 f(at) a 频移 f(t)e-a F(s+a) 微分 df(t)》 SF(s)-f(0) dt 积分 ∫f(r)dr F(s)) S S
12 5.3 拉氏变换的基本性质(1) 线性 ( ) 1 k f t i n i i . [ ( )] 1 k LT f t n i i dt df (t) 微分 ( ) (0 ) SF s f 积分 t f ( ) d s f s F(s) (0 ) 1 时移 ( ) ( ) 0 0 f t t u t t ( ) 0 e F s st 频移 at f t e ( ) F(s a) 尺度变换 f (at) a s F a 1

拉氏变换的基本性质(2) 尺度变换 f(at) 初值定理 lim f(t)=f(0*)=lim SF(s) 1->0 S→00 终值 定理 (()limSF(s) 5-→0 (t)*() F,(s)·F2(s) 卷积 定理 f()·f2(t) F(s)*F2(S) 2nj 13
13 拉氏变换的基本性质(2) 尺度变换 f (at) a s F a 1 lim ( ) (0 ) lim ( ) 0 f t f SF s t s 终值 定理 lim ( ) ( ) lim ( ) 0 f t f SF s t s 卷积 定理 ( )* ( ) 1 2 f t f t ( ) ( ) 1 2 F s F s 初值定理 ( ) ( ) 1 2 f t f t ( ) * ( ) 2 1 1 2 F s F s j