
Chapter 3Methods of AnalysisSJTU
SJTU 1 Chapter 3 Methods of Analysis

So far, we have analyzed relatively simple circuits byapplying Kirchhoff's laws in combination with Ohm's law.We can use this approach for all circuits, but as theybecome structurally more complicated and involve moreand more elements, this direct method soon becomescumbersome. In this chapter we introduce two powerfultechniques of circuit analysis: Nodal Analysis and MeshAnalysis.These techniques give us two systematic methods ofdescribing circuits with the minimum number ofsimultaneous equations. With them we can analyze almostany circuit by to obtain the required values of current orvoltage.2SJTU
SJTU 2 So far, we have analyzed relatively simple circuits by applying Kirchhoff’s laws in combination with Ohm’s law. We can use this approach for all circuits, but as they become structurally more complicated and involve more and more elements, this direct method soon becomes cumbersome. In this chapter we introduce two powerful techniques of circuit analysis: Nodal Analysis and Mesh Analysis. These techniques give us two systematic methods of describing circuits with the minimum number of simultaneous equations. With them we can analyze almost any circuit by to obtain the required values of current or voltage

Nodal AnalysisStepstoDetermineNodeVoltages1.Select a node as the reference node(ground), define the node voltages1,2,..n- to the remaining n- nodes. The voltages arereferenced with respectto the reference node.2.ApplyKCL to each of the n-1 independentnodes.Use Ohm's law toexpressthebranchcurrents intermsofnodevoltages.3.Solvethe resulting simultaneousequationsto obtaintheunknownnodevoltages3SJTU
SJTU 3 Nodal Analysis • Steps to Determine Node Voltages: 1. Select a node as the reference node(ground), define the node voltages 1 , 2 ,. n-1 to the remaining n-1nodes . The voltages are referenced with respect to the reference node. 2. Apply KCL to each of the n-1 independent nodes. Use Ohm’s law to express the branch currents in terms of node voltages. 3. Solve the resulting simultaneous equations to obtain the unknown node voltages
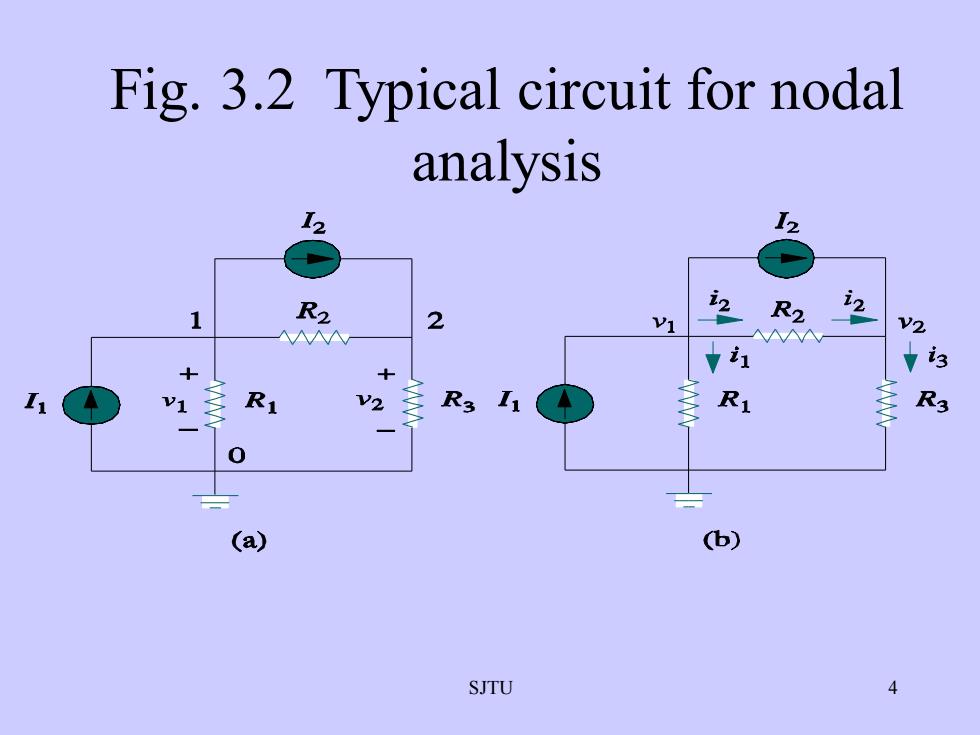
Fig. 3.2 Typical circuit for nodalanalysis15ini2R2R227V1V2订i3R1R3R1I1R3V2V1-0(b)(a)SJTU
SJTU 4 Fig. 3.2 Typical circuit for nodal analysis
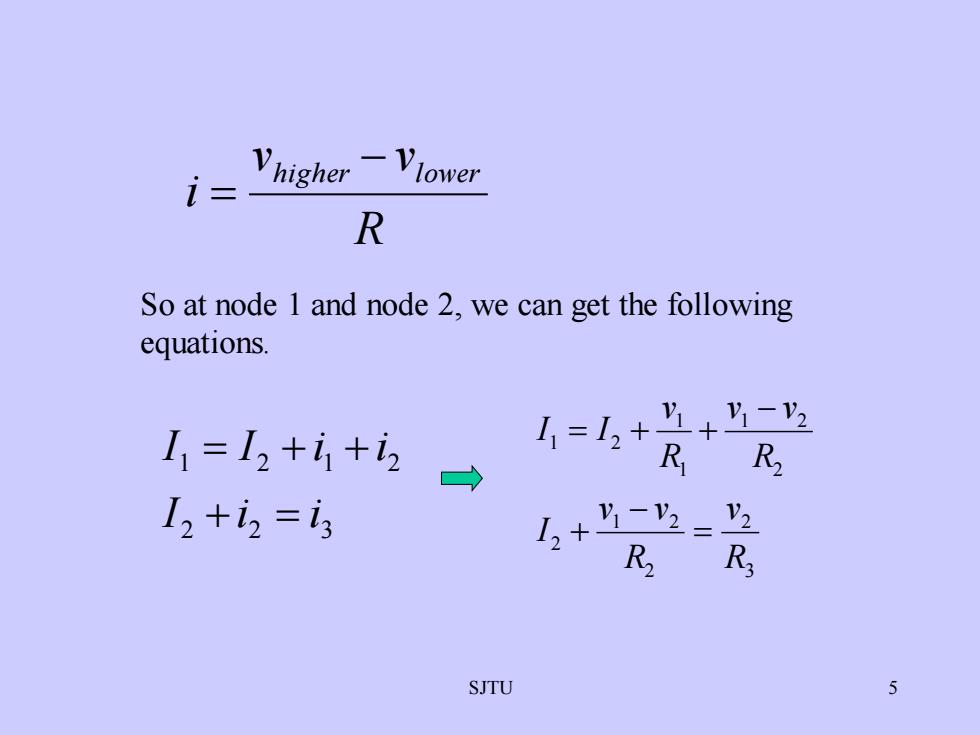
VlowerhigherRSo at node 1 and node 2, we can get the followingequationsV1V.-VI, = I2 +i +izRR2V2I2 +iz =is+V1-V2L.+R2R3SJTU5
SJTU 5 R v v i higher − lower = So at node 1 and node 2, we can get the following equations. 3 2 2 1 2 2 2 1 2 1 1 1 2 R v R v v I R v v R v I I = − + − = + + 2 2 3 1 2 1 2 I i i I I i i + = = + +