
(1)偶函数 f(t)=f(-t) f()sin no idt 2 oaw-22w 1 T T 27 eaah-专0 o 2 所以,在偶函数的傅里叶级数中不会有正弦项,只可能 含有(直流)和余弦分量
(1)偶函数 f (t) = f (−t) = = − 2 0 1 1 2 2 1 1 1 1 1 ( ) cos 4 ( ) cos 2 T T n T f t n tdt T f t n tdt T a 1 1 2 1 1 2 2 ( )sin 0 T b f t n tdt n T T − = = 所以,在偶函数的傅里叶级数中不会有正弦项,只可能 含有(直流)和余弦分量。 = = − 2 0 1 2 1 2 0 1 1 1 ( ) 2 ( ) 1 T T T f t dt T f t dt T a

(2)奇函数 f(t)=-f(-t) fOd-0 an 二T27 ∫f0 cosno,tdh=0 2 sna=户snm 2 在奇函数的傅里叶级数中不会含有直流与余弦分量,只可能包含 正弦分量。 (3)奇谐函数 fu+)=-f0 或 -u±3)=0
(2)奇函数 f (t) = − f (−t) 1 1 1 2 2 1 1 0 1 1 2 2 4 ( )sin ( )sin T T b f t n tdt f t n tdt n T T T − = = 在奇函数的傅里叶级数中不会含有直流与余弦分量,只可能包含 正弦分量。 (3)奇谐函数 ) ( ) 2 ( 1 f t T f t = − 或 ) ( ) 2 ( 1 f t T − f t = 1 1 2 0 1 2 1 ( ) 0 T a f t dt T T − = = 1 1 2 1 1 2 2 ( )cos 0 T a f t n tdt n T T − = =
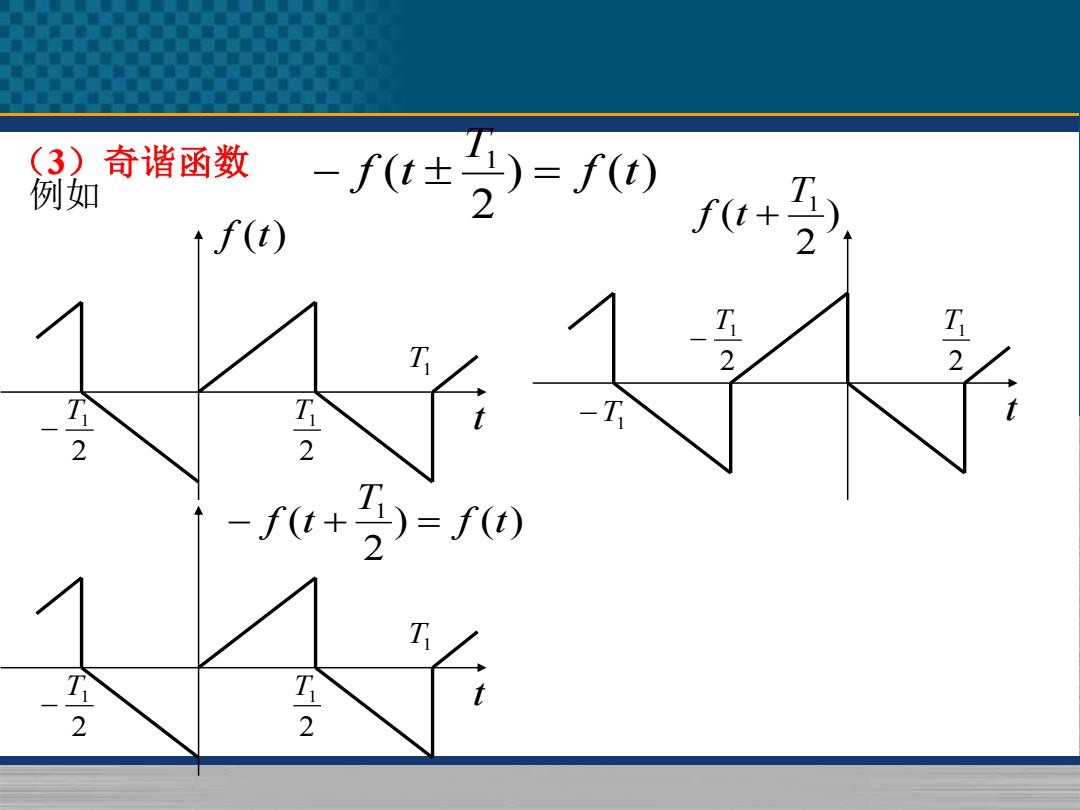
(3)奇谐函数 例如 -f+分=0u+ if(t) 2 7 .4 2 2 2 -u+=0 T t 2 2
(3)奇谐函数 ) ( ) 2 ( 1 f t T − f t = f (t) t 2 T1 T1 2 T1 − 例如 ) 2 ( T1 f t + t 2 T1 −T1 2 T1 − ) ( ) 2 ( 1 f t T − f t + = t 2 T1 T1 2 T1 −

a0= 0 (n=2,4,6…) An 4 Ty (n=1,3,5…) T f()cosnmtdt (n=2,4,6) b.)i o (n=1,3,5…) 可见,在奇谐函数的傅里叶级数中,只会含有基波和奇次 谐波的正弦、余弦分量,而不会包含直流和偶次谐波分量
= = = ( )cos ( 1,3,5 ) 4 0 ( 2,4,6 ) 2 0 1 1 1 f t n tdt n T n a T n = = = 2 0 1 1 1 ( )sin ( 1,3,5 ) 4 0 ( 2,4,6 ) T n f t n tdt n T n b 可见,在奇谐函数的傅里叶级数中,只会含有基波和奇次 谐波的正弦、余弦分量,而不会包含直流和偶次谐波分量。 a0 = 0
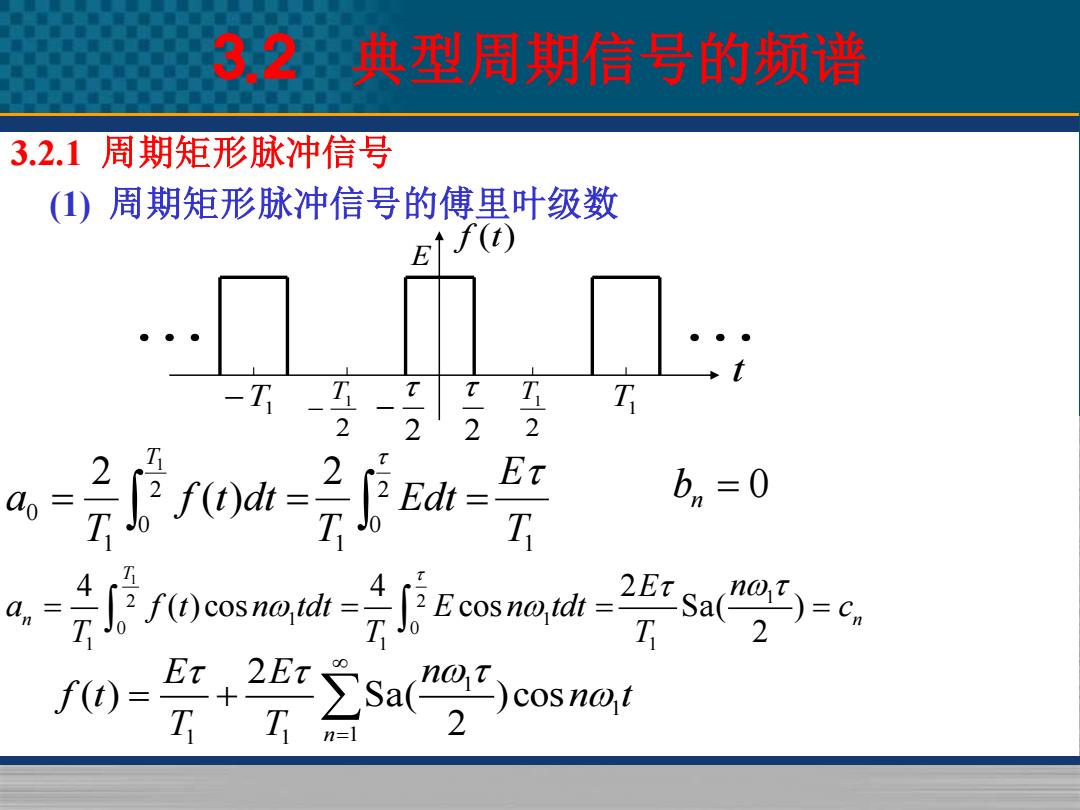
3,2典型周期信号的频谱 3.2.1周期矩形脉冲信号 (1)周期矩形脉冲信号的傅里叶级数 EJ() -T 2 2 -2 T 2 2 Et Edt b,=0 T T an f)= Et 2Et n=1
3.2 典型周期信号的频谱 3.2.1 周期矩形脉冲信号 (1) 周期矩形脉冲信号的傅里叶级数 t f (t) 2 2 − 2 T1 2 T1 −T1 − T1 E 1 2 0 1 2 0 1 0 2 ( ) 2 1 T E Edt T f t dt T a T = = = = 0 n b 1 2 2 1 1 1 0 0 1 1 1 4 4 2 ( )cos cos Sa( ) 2 T n n E n a f t n tdt E n tdt c T T T = = = = 1 1 1 1 1 2 ( ) Sa( )cos n 2 E E n f t n t T T = = +