
3.1.3周期信号的频谱及其特点 1.周期信号的频谱 f(t)=ao+>(a,cosn@t+b sin not) (1) n= f)=c+∑c,cos(no,t+0) (2) n= f(t)=∑Fne (3) f)→Fn建立一一对应关系。 不同时域信号对应的Fn不同,因此可以通过研究Fn来研究 信号的特性。F是频率的函数,它反映了组成信号的各次谐波的幅 度和相位变化规律称为频谱函数。直接画出各次谐波对应的F的线 状分布图形称为信号的频谱图
3.1.3 周期信号的频谱及其特点 1. 周期信号的频谱 =− = n j n t f t Fn e 1 ( ) (3) = = + + 1 0 1 1 ( ) ( cos sin ) n n n f t a a n t b n t (1) = = + + 1 0 1 ( ) cos( ) n n n f t c c n t (2) f(t) →Fn建立一一对应关系。 不同时域信号对应的Fn不同,因此可以通过研究Fn来研究 信号的特性。Fn是频率的函数,它反映了组成信号的各次谐波的幅 度和相位变化规律称为频谱函数。直接画出各次谐波对应的Fn的线 状分布图形称为信号的频谱图

Fnt ·例题:已知信号f(t)=cos100t,求其频谱Fn。 0.5 f0-ew+eu) 1 解: =6= -W1W1 nw1 所以 其余Fn=0,n≠±l ·例题:已知信号f(t)的频谱Fn如图所示,求信号f(t)。 解: F=2,F1=F=2,F2=F2=1 ,1 00 所以f0)=∑Fem ,1 -2w1 -W1 w1 2w1 nw1 1=-00 -2+2e+2eee =2+4cosw t+2cos2w t
• 例题:已知信号f(t)=cos100t,求其频谱Fn。 其余Fn = 0,n 1 解: ( ) 2 1 ( ) j100t j100t f t e e − = + , 2 1 所以 F−1 = F1 = • 例题:已知信号f(t)的频谱Fn如图所示,求信号f(t)。 解: 2, 2, 1 F0 = F−1 = F1 = F−2 = F2 = 所以 - 2w1 -w1 w1 2w1 nw1 Fn 2 2 1 j w t j w t j w t j w t n jnwt n e e e e f t F e 1 1 1 1 1 2 2 2 2 2 ( ) − − + =− = + + + + = w t w t 1 2 1 = 2 + 4cos + 2cos -w1 w1 nw1 Fn 0.5
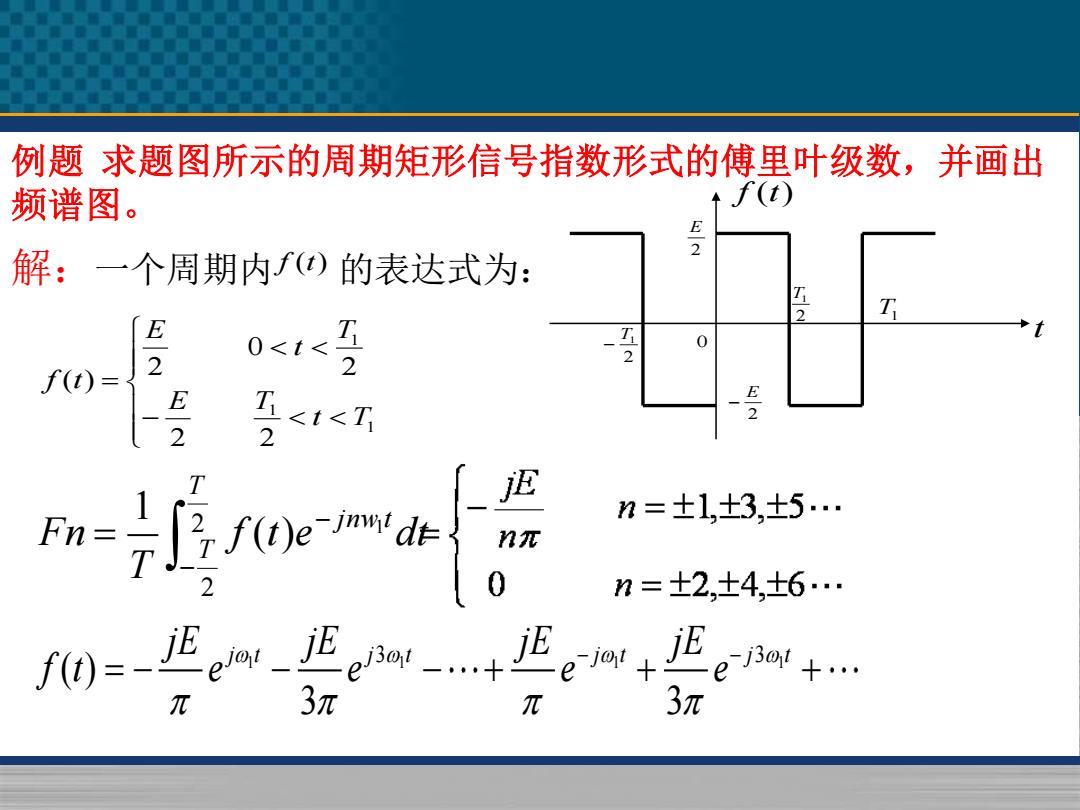
例题求题图所示的周期矩形信号指数形式的傅里叶级数,并画出 频谱图。 f(t) E 解:一个周期内()的表达式为: 2 T E2 0<t< 0 2 f(t) = E-2 2 <t<T n=士1,±3,±5… n元 n=±2,±4,±6… f)iaEe π 3元 π 3元
例题 求题图所示的周期矩形信号指数形式的傅里叶级数,并画出 频谱图。 解:一个周期内 f (t) 的表达式为: − = 1 1 1 2 2 2 0 2 ( ) t T E T T t E f t 2 E 2 E − 2 T1 − 2 T1 0 f (t) t T1 1 1 1 1 3 3 ( ) 3 3 j t j t j t j t jE jE jE jE f t e e e e − − = − − − + + + f t e dt T F n T T jnwt − − = 2 2 1 ( ) 1

E 2 (n=1,3,5…) (n=±l,±3,±5…) nπ 二 幅度频谱和相位频谱 (n=-1,-3,-5…) E E E π 3π 频谱的特点 5π 501 离散性 π 谐波性 2 -501-301-01 30500 收敛性 π 2
( 1,3,5 ) 2 ( 1, 3, 5 ) 2 n n n − = = = − − − ( 1, 3, 5 ) n E F n n = = Fn E 3 E 5 E 1 1 3 1 −51 −31 −1 5 2 − 2 n −51 −31 −1 1 1 3 1 5 幅度频谱和相位频谱 离散性 谐波性 收敛性 频谱的特点

2.周期信号频谱的特点 (1)离散性---频谱是离散的而不是连续的,这种频谱称为 离散频谱 (2)谐波性 谱线出现在基波频率O1的整数倍上。 (3)收敛性 --- 幅度谱的谱线幅度随着n→o∞1 而逐渐 衰减到零。 3.1.4波形的对称性与谐波特性的关系 如果孔)是实函数而且它的波形满足某种对称性,则在傅里叶级 数中有些项将不出现,留下的各项系数的表示式也将变得比较 简单
2. 周期信号频谱的特点 (1)离散性-------- 频谱是离散的而不是连续的,这种频谱称为 离散频谱 (2)谐波性-------- 谱线出现在基波频率 1 的整数倍上。 (3)收敛性-------- 幅度谱的谱线幅度随着 而逐渐 衰减到零。 n → 3.1.4 波形的对称性与谐波特性的关系 如果f(t)是实函数而且它的波形满足某种对称性,则在傅里叶级 数中有些项将不出现,留下的各项系数的表示式也将变得比较 简单