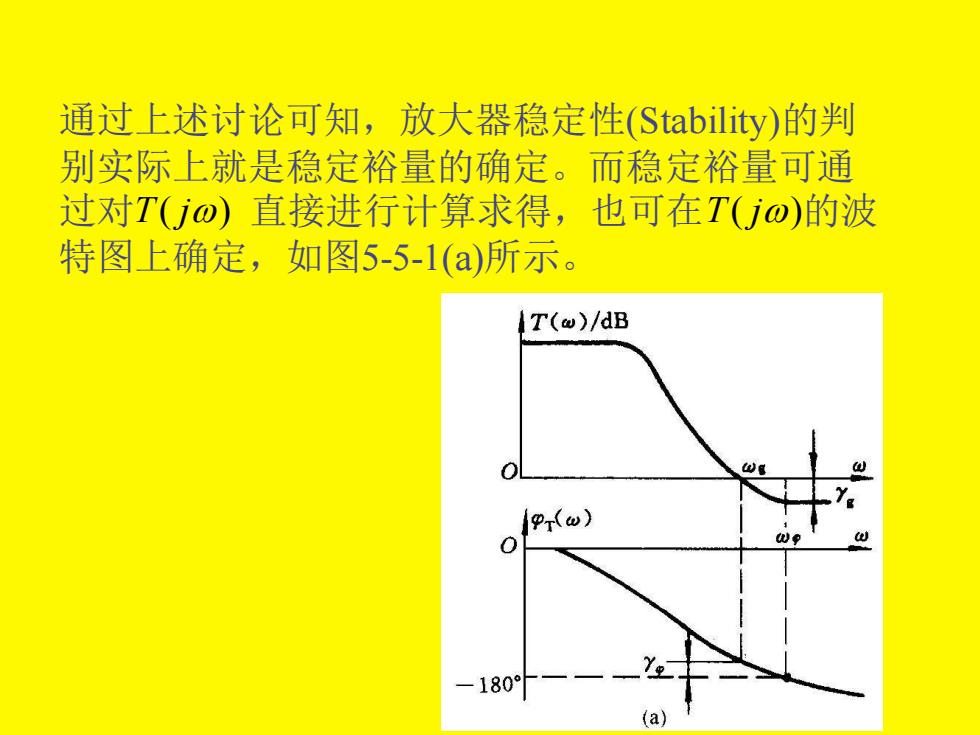
通过上述讨论可知,放大器稳定性(Stability)的判 别实际上就是稳定裕量的确定。而稳定裕量可通 过对T(Ujo)直接进行计算求得,也可在T(jo)的波 特图上确定,如图5-5-1(a)所示。 T(@)/dB Pr(ω) -180 (a)
通过上述讨论可知,放大器稳定性(Stability)的判 别实际上就是稳定裕量的确定。而稳定裕量可通 过对 直接进行计算求得,也可在 的波 特图上确定,如图5-5-1(a)所示。 T( j) T( j)

如果放大器施加的是电阻性反馈, k,为实数,则将T(og)=krA(o)=1写成: A(@g)=1/ky 或 20gA(og)=20g/k, (5-5-6) 就可在基本放大器的幅频特性波特图上作高度为 201g1/k(dB)的水平线,如图5-5-2所示
如果放大器施加的是电阻性反馈, k f 为实数,则将T(g ) = k f A(g ) =1写成: g f A( ) =1 k 或 g f 20lg A( ) = 20lg1 k (5-5-6) 就可在基本放大器的幅频特性波特图上作高度为 20lg1/kf(dB)的水平线,如图5-5-2所示
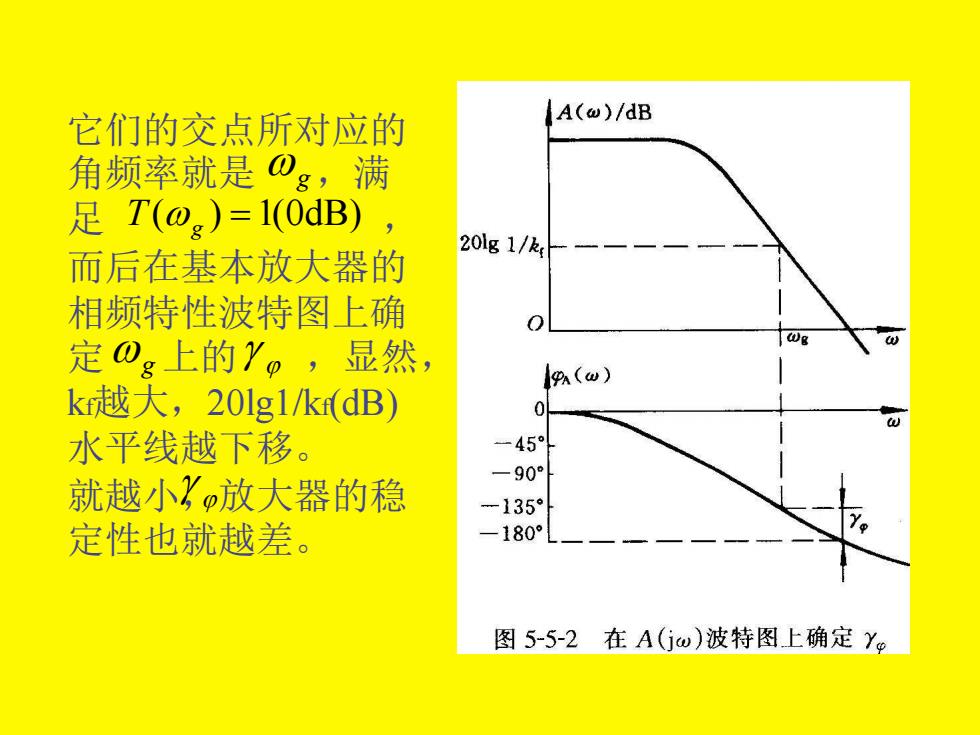
它们的交点所对应的 A(w)/dB 角频率就是0g,满 足T(o.)=1(0dB), 而后在基本放大器的 20lg1/k- 相频特性波特图上确 0 定Dg上的Y。,显然, l9(w) k越大,20lg1/kdB) 0 水平线越下移。 -45° 一90° 就越小?o放大器的稳 -135° 定性也就越差。 -180° 图5-5-2在A(Gw)波特图上确定Y2
它们的交点所对应的 角频率就是 ,满 足 , 而后在基本放大器的 相频特性波特图上确 定 上的 ,显然, kf越大,20lg1/kf(dB) 水平线越下移。 就越小,放大器的稳 定性也就越差。 g ( ) =1(0dB) T g g

在A(⊙)波特图上确定稳定裕量时,若遇到基本放大 器为反相放大器的情况,则由于中频区为负反馈, Ak为正值,因而A为负值,k也就必定为负值。这 样,在画A(j⊙)的相频特性时,为了简化起见,就 不必计入180°相移。同时,k的负号也可相应删去。 若中频区满足深度负反馈,则1k就是反馈放大器 的中频增益。故1水平线又称为反馈增益线
在 波特图上确定稳定裕量时,若遇到基本放大 器为反相放大器的情况,则由于中频区为负反馈, AIkf为正值,因而AI为负值,kf也就必定为负值。这 样,在画 的相频特性时,为了简化起见,就 不必计入180º相移。同时,kf的负号也可相应删去。 A( j) A( j) 若中频区满足深度负反馈,则1/kf就是反馈放大器 的中频增益。故1/kf水平线又称为反馈增益线

三、在幅频特性渐近波特图上 判别稳定性 在某些情况下,可以采用直接在T(jo)或A(jo) 的幅频特性渐近波特图上判别稳定性的简化方法。 假设T()o)为无零高阶系统,且它的各极点角频率依 次为0p1,0p2,0p3,,则如前述,其幅频特性渐近 波特图将自中频增益开始,每经过一个极点角频率, 下降段的斜率增加20dB/十倍频。而相频特性渐近波 特图则与各极点角频率的相对间距有关。以 A(jo) 为例,图5-5-3示出了三极点系统, 且 0p3=10op2,0p2=l00p1 的渐近波特图
三、在幅频特性渐近波特图上 判别稳定性 在某些情况下,可以采用直接在 或 的幅频特性渐近波特图上判别稳定性的简化方法。 T( j) A( j) 假设 为无零高阶系统,且它的各极点角频率依 次为 .,则如前述,其幅频特性渐近 波特图将自中频增益开始,每经过一个极点角频率, 下降段的斜率增加20dB/十倍频。而相频特性渐近波 特图则与各极点角频率的相对间距有关。以 为例,图5-5-3示出了三极点系统, 且 , 的渐近波特图。 T( j) , , , P1 P2 P3 A( j) P3 =10P2 P2 =10P1