
Z一复阻抗;☑一复阻抗的模;p2一 阻抗角; R一电阻(阻抗的实部);X一电抗(阻抗的虚部)。 转换关系: .=arctan R R=☑cos0: U 或 X=Zsing. p.=Ψ。-Ψ 阻抗三角形
Z — 复阻抗;|Z| —复阻抗的模;z —阻抗角; R —电阻(阻抗的实部);X—电抗(阻抗的虚部)。 转换关系: arctan | | 2 2 R X φ Z R X z 或 R=|Z|cosz X=|Z|sinz 阻抗三角形 |Z| R X z z u i I U Z 返 回 上 页 下 页
分析R、L、C串联电路得出 (1) Z=R+j(oL-1/oC=Z∠p,为复数,称复阻抗 (2) oL>1/oC,0,p,>0,电路为感性, 电压超前电流。 相量图:一般选电流为参考向量, 4,=0 电压 U 三角 形 Ux 等效电路
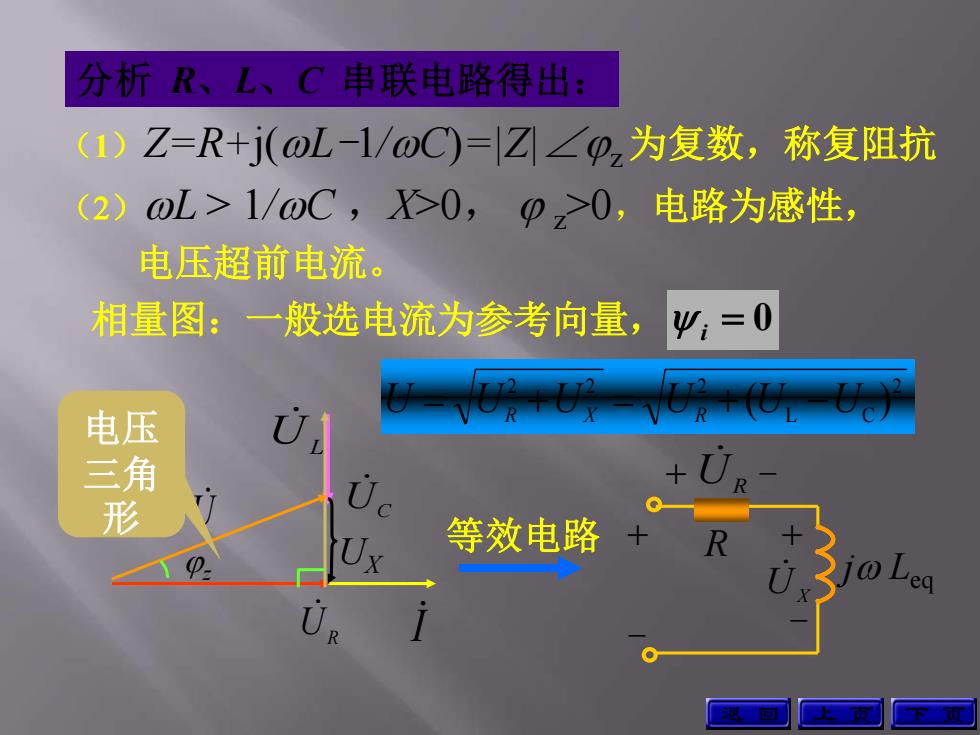
I 分析 R、L、C 串联电路得出: (1)Z=R+j(L-1/C)=|Z|∠z 为复数,称复阻抗 (2)L > 1/C ,X>0, z>0,电路为感性, 电压超前电流。 i 0 上 页 下 页 相量图:一般选电流为参考向量, UC UR UL U z UX 电压 三角 形 2 L C 2 2 2 U U U U (U U ) R X R j Leq UX + R - + - + UR - 等效电路 返 回
(3) oL<1/oC,X<0,p,<0,电路为容性, 电压落后电流。 U 等效电路 R j@Ce (4)oL=1/o0C,X=0,p,=0,电路为电阻性, 电压与电流同相。 等效电路
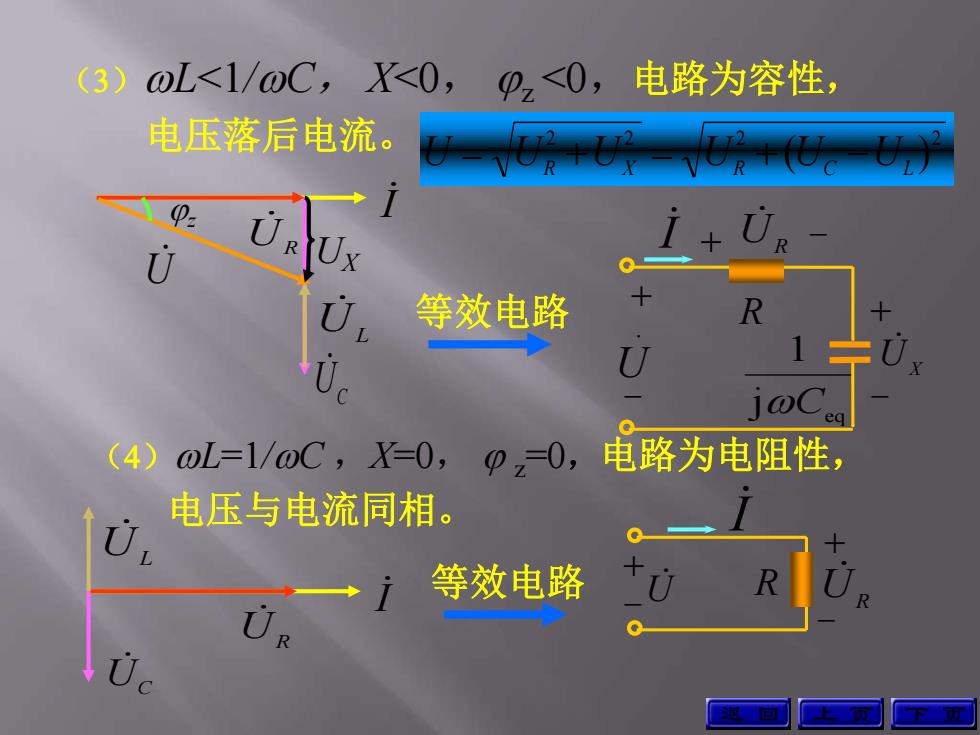
I (3)L<1/C, X<0, z <0,电路为容性, 电压落后电流。 UC UR UL U z UX 等效电路 上 页 下 页 UX eq j 1 C R + - + - + UR - . U I (4)L=1/C ,X=0, z=0,电路为电阻性, 电压与电流同相。 I UR UL UC R + - + - I UR 等效电路 U 2 2 2 2 ( ) U UR UX UR UC UL 返 回

例 已知:R=152,L-0.3mH,C=0.2uF, u=5V2cos(o+60),f=3×10Hz. 求i,4g,山,C: R 1o! 解 画出相量模型 U=5∠60°V j0L=j2π×3×104×0.3×103 =j56.52 2元×3×104×0.2×106 =-j26.50 Rjow ,=15+j56.5-j26.5 =33.54∠63.4°2 回
例 已知:R=15, L=0.3mH, C=0.2F, 5 2cos( 60 ), 3 10 Hz . 4 u t f 求 i, uR , uL , uC . 解 画出相量模型 5 60 V U C Z R L 1 j j j56.5Ω j j2π 3 10 0.3 10 4 3 L j26.5Ω 2π 3 10 0.2 10 1 j 1 j 4 6 C 15 j56.5 j26.5 33.54 63.4 Ω o 上 页 下 页 L C R u uL uC i + - + - + - + - uR R + - + - + - + - . I j L U UL U C . jC 1 UR 返 回

i= 5∠60° =0.149∠-3.4°A Z33.54∠63.4° UR=Ri=15×0.149∠-3.4°=2.235∠-3.4°V 0L=joLi=56.5∠90°×0.149∠-3.4°=8.42∠86.4°V 0c=-j1=26.5∠-90°x0.149∠-3.4°=3.95∠-93.4°V 则 i=0.149N2c0s(ot-3.4)A ug =2.2352cos(@t-3.4)V u,=8.42√2cos(wt+86.6)V u=3.95V2c0s(wt-93.4)V 回 上
0.149 3.4 A 33.54 63.4 5 60 o o o Z U I 则 i 0.149 2cos(ωt 3.4 o ) A 15 0.149 3.4 2.235 3.4 V o o U R RI j 56.5 90 0.149 3.4 8.42 86.4 V o o o U L LI 26.5 90 0.149 3.4 3.95 93.4 V C 1 j o o o U C I 2.235 2cos( 3.4 ) V o uR ω t 8.42 2cos( 86.6 ) V o uL ω t 3.95 2cos( 93.4 ) V o uC ω t 返 回 上 页 下 页