
电路一阶电路和二阶电路的时域分析山③电感的初始条件u()d. (t)L-81u()d= + -u())d厂J-Lu()d§=i(0.)+-JOLu()di(0)=i,(0.)+t=0+时刻L当u为有限值时返上回页下页
()d 1 ( ) − = t L u L i t ())d 1 ( )d 1 0 0 − − = + − t u L u L ()d 1 (0 ) (0 ) 0 0 + − + = − + u L i i L L ③电感的初始条件 t = 0+时刻 0 ()d 1 (0 ) 0− = − + t L u L i 上 页 下 页 当u为有限值时 iL u L + - 返 回

电路一阶电路和二阶电路的时域分析山磁链i(0+)=i(0_)守恒W = LiVL(O+)= i(0_)结论换路瞬间,若电感电压保持为有限值,则电感电流(磁链)换路前后保持不变返上回页下页
L (0+)= L (0-) iL (0+)= iL (0-) = LiL 磁链 守恒 换路瞬间,若电感电压保持为有限值, 则 电感电流(磁链)换路前后保持不变。 上 页 下 页 结论 返 回

电路一阶电路和二阶电路的时域分析山④换路定律换路瞬间,若电容电流保持为qc(0+) = qc(0_)有限值,则电容电压(电荷)换uc(O.) = uc(0_)路前后保持不变换路瞬间,若电感电压保持Vi(0+)= Vi(0-)为有限值,则电感电流(磁链i(0.)=i(0_)换路前后保持不变①电容电流和电感电压为有限值是换路定注意律成立的条件②换路定律反映了能量不能跃变。返上回页下页
L (0+ )= L (0-) iL (0+ )= iL (0-) qc (0+ ) = qc (0-) uC (0+ ) = uC (0-) ④换路定律 ①电容电流和电感电压为有限值是换路定 律成立的条件。 换路瞬间,若电感电压保持 为有限值,则电感电流(磁链) 换路前后保持不变。 换路瞬间,若电容电流保持为 有限值,则电容电压(电荷)换 路前后保持不变。 ②换路定律反映了能量不能跃变。 上 页 下 页 注意 返 回
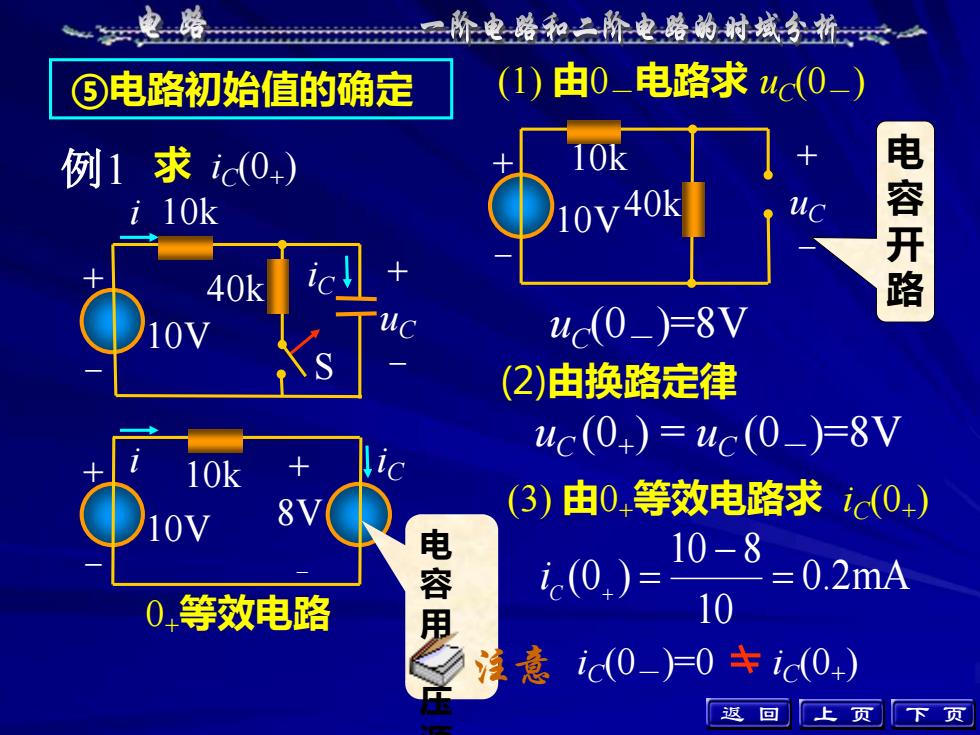
电路一阶电路和二阶电路的时域分折山(1)由0_电路求 uc(0_)③电路初始值的确定电容开路10k例1 求 ic(0)10v40ki 10k40kuc(0_)=8V10V(2)由换路定律uc(0+) = uc(0_)=8V+1O10k(3)由0.等效电路求ic(0+)8V10V电容用10-8= 0.2mAic(0)100.等效电路ic(0_)=0 ± ic(0+)注意返上回页入页
⑤电路初始值的确定 (2)由换路定律 uC (0+ ) = uC (0-)=8V 0.2mA 10 10 8 (0 ) = − i C + = (1) 由0-电路求 uC(0-) uC (0-)=8V (3) 由0+等效电路求 iC(0+ ) iC(0-)=0 iC(0+ ) 例1 求 iC(0+ ) 电 容 开 路 上 页 下 页 + - 10V i iC + uC S - 10k 40k + - 10V + uC - 10k 40k + 8V - 0+等效电路 + - 10V i 10k iC 电 容 用 电 压 源 注意 返 回
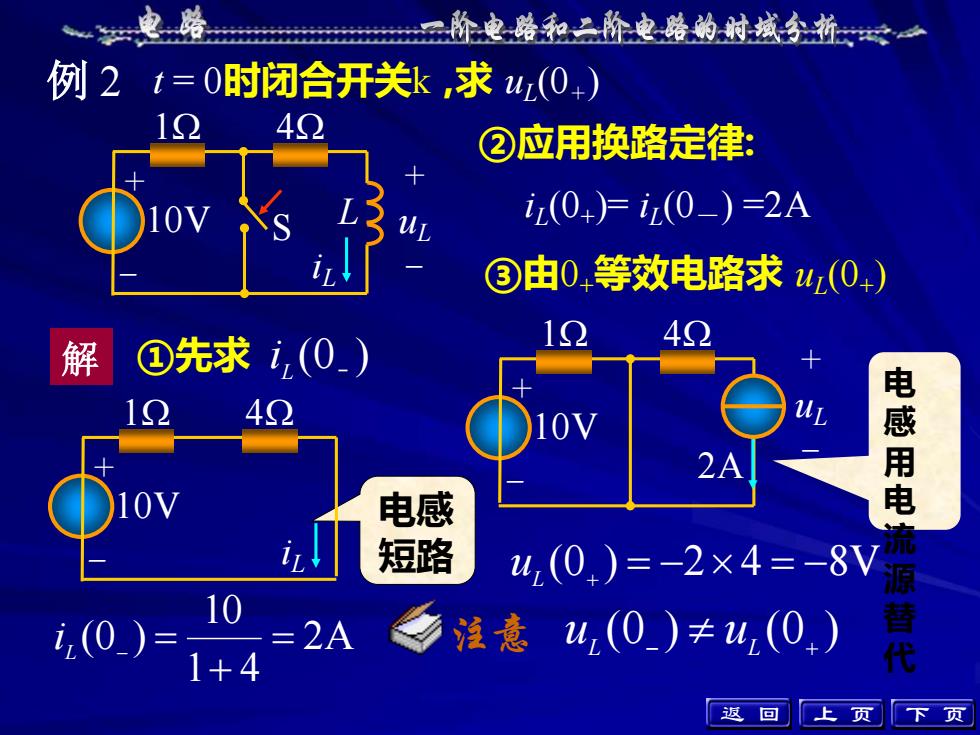
电路阶电路和二阶电路的时域分析例 2 t=0时闭合开关k,求ur(0+)124Q②应用换路定律:i(0+)= i(0_)=2A10VM③由0.等效电路求ui(0+)1Q42解①先求i(0.)十电感用电流源替代UL124210V2A十10V电感短路u,(0.)=-2×4= -8V10u,(0_)±u,(0)注意2Ai.(O_)1+ 4返上回页下页
(0 ) (0 ) L − L + u u iL (0+ )= iL (0-) =2A uL (0+ ) = −2 4 = −8V 例 2 t = 0时闭合开关k ,求 uL (0+) ①先求 2A 1 4 10 (0 ) = + i L − = ②应用换路定律: 电 感 用 电 流 源 替 代 (0 − ) L 解 i 电感 短路 上 页 下 页 iL + uL - 10V L S 1 4 + - iL 10V 1 4 + - ③由0+等效电路求 uL (0+ ) 2A + uL - 10V 1 4 + - 注意 返 回