
电路一阶电路和二阶电路的时域分析山一阶有源结论一个动电路电阻态元件电路含有一个动态元件电容或电感的线性电路,其电路方程为一阶线性常微分方程,称一阶电路。返上回页下页
有源 电阻 电路 一个动 态元件 一阶 电路 上 页 下 页 结论 含有一个动态元件电容或电感的线性电 路,其电路方程为一阶线性常微分方程,称 一阶电路。 返 回
电路一阶电路和二阶电路的时域分析RiRLC电路(t >0)应用KVL和元件的VCR得:Ri +u, +uc =us(t)udiducOu=LCu, =Li=二阶电路dt?dtdtducduLCRC+uc =u,(t)dtdt含有二个动态元件的线性电路,其电路方程为二阶线性常微分方程,称二阶电路。返上回页下页
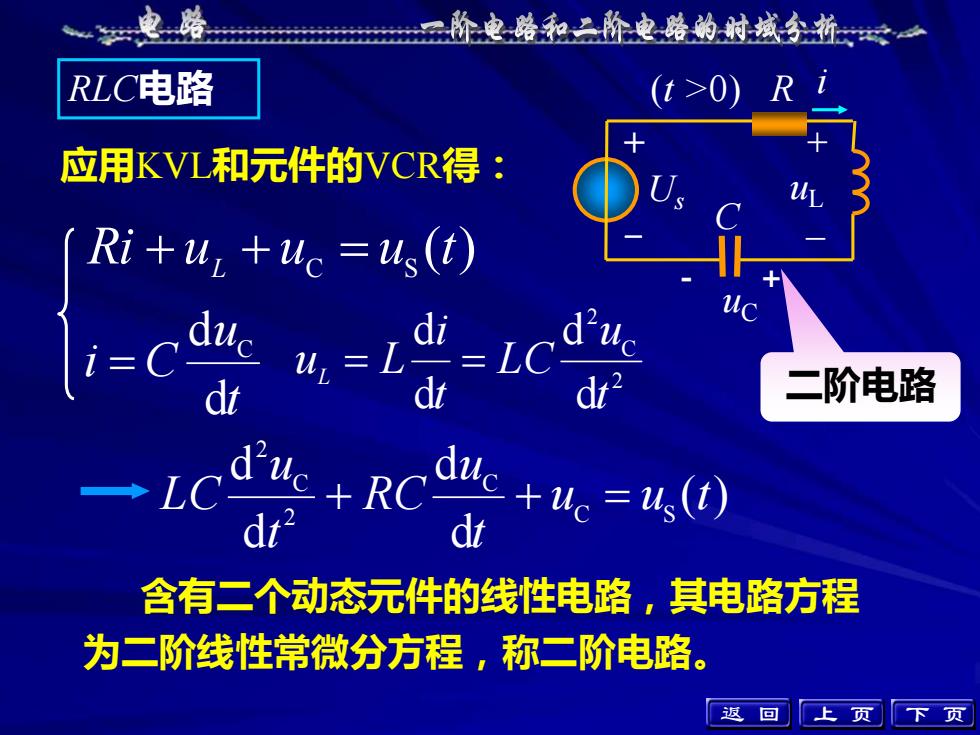
( ) d d d d C S C 2 C 2 u u t t u R C t u L C + + = ( ) C S Ri u u u t + L + = t 二阶电路 u i C d d C = 2 C 2 d d d d t u LC t i uL = L = 上 页 下 页 (t >0) + – Us uL R i + - C uC - + RLC电路 应用KVL和元件的VCR得: 含有二个动态元件的线性电路,其电路方程 为二阶线性常微分方程,称二阶电路。 返 回

电路一阶电路和二阶电路的时域分析山①描述动态电路的电路方程为微分方程;结论②动态电路方程的阶数通常等于电路中动态元件的个数。一→一阶电路中只有一个动态元件,描述一阶电路电路的方程是一阶线性微分方程dxt≥0+ a.x =e(t)adt阶电路二阶电路中有二个动态元件,描述电路的方程是二阶线性微分方程QdxXt≥0+a,x=e(t+ addt?dt返上回页T页
一阶电路 一阶电路中只有一个动态元件,描述 电路的方程是一阶线性微分方程。 ①描述动态电路的电路方程为微分方程; ②动态电路方程的阶数通常等于电路中动 态元件的个数。 ( ) 0 d d 1 + a0 x = e t t t x a ( ) 0 d d d d 2 1 0 2 2 + + a x = e t t t x a t x a 二阶电路 二阶电路中有二个动态元件,描述电 路的方程是二阶线性微分方程。 上 页 下 页 结论 返 回

电路一阶电路和二阶电路的时域分析山电路中有多个动态元件,描述高阶电路电路的方程是高阶微分方程。d"xdxdxt≥0+a.x =e(t)aadtn-Ydtn-1dtn动态电路的分析方法①根据KVL、KCL和VCR建立微分方程;返上回页下页
高阶电路 电路中有多个动态元件,描述 电路的方程是高阶微分方程。 ( ) 0 d d d d d d 1 1 0 1 + 1 + + + = − − − a x e t t t x a t x a t x a n n n n n n 动态电路的分析方法 ①根据KVL、KCL和VCR建立微分方程; 返 回 上 页 下 页

电路一阶电路和二阶电路的时域分析山②求解微分方程复频域分析法时域分析法本章采用经典法拉普拉斯变换法状态变量法状态变量法卷积积分付氏变换数值法工程中高阶微分方程应用计算机辅助分析求解返上回页下页
时域分析法 复频域分析法 ②求解微分方程 经典法 状态变量法 数值法 卷积积分 拉普拉斯变换法 状态变量法 付氏变换 本章 采用 工程中高阶微分方程应用计算机辅助分析求解。 返 回 上 页 下 页