
矢量场的通量与散度 -Note1:通量可以叠加; -Note2:直角坐标系中: 11
lexu@mail.xidian.edu.cn 矢量场的通量与散度 – Note1:通量可以叠加; – Note2:直角坐标系中: 11

矢量场的通量与散度 ·物理意义 一开曲面 ·当Q>0:流向正侧流量多于流向负侧流量; ·当Q<0:流向正侧流量少于流向负侧流量: ·当Q=0:流向正侧流量等于流向负侧流量。 一闭曲面 ·当Q>0:穿出的通量大于穿入的通量,有正源; ·当Q<0:穿出的通量小于穿入的通量,有负源; ·当Q=0:穿出的通量等于穿入的通量,正、负源抵消或无源。 lexu@mail.xidian.edu.cn 12
矢量场的通量与散度 • 物理意义 – 开曲面 • 当Q>0:流向正侧流量多于流向负侧流量; • 当Q<0:流向正侧流量少于流向负侧流量; • 当Q=0:流向正侧流量等于流向负侧流量。 – 闭曲面 • 当Q>0:穿出的通量大于穿入的通量,有正源; • 当Q<0:穿出的通量小于穿入的通量,有负源; • 当Q=0:穿出的通量等于穿入的通量,正、负源抵消或无源。 lexu@mail.xidian.edu.cn 12
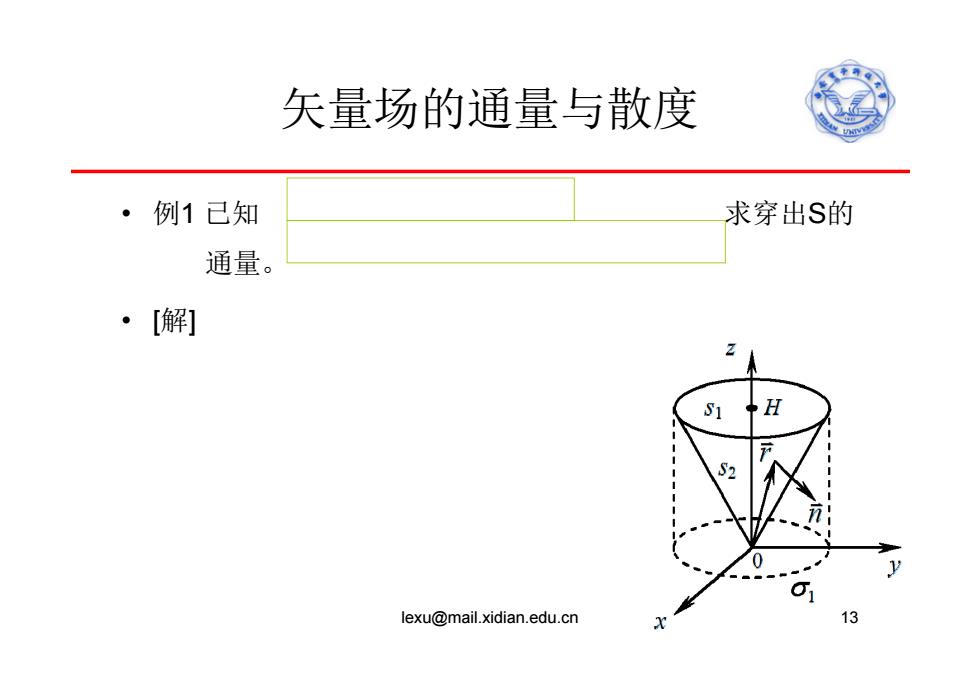
矢量场的通量与散度 ·例1已知 求穿出S的 通量。 ·[解] H lexu@mail.xidian.edu.cn 13
矢量场的通量与散度 • 例1 已知 求穿出 S 的 通量。 • [ 解 ] lexu@mail.xidian.edu.cn 13

矢量场的通量与散度 ·例2原点处点电荷q在其周围产生的电场中,任一点 处的电位移矢量 ), 求穿过以原点为球心,R为半径球面的电通量。 ·[解] s内产生电通量 的源即为电荷q 14
lexu@mail.xidian.edu.cn 矢量场的通量与散度 • 例2 原点处点电荷q在其周围产生的电场中,任一点 处的电位移矢量 ( ), 求穿过以原点为球心,R为半径球面的电通量。 • [解] 14 s内产生电通量 的源即为电荷q

矢量场的通量与散度 ·矢量场的散度 全局特性 局部特性 一为表征矢量 曲面内有 源在s内 场内一点处 正源或负源 分布情况及 一点处强弱 源的强弱而 V(M) 引入散度的 概念! 闭合曲面 通量正负 散度 lexu@mail.xidian.edu.cn 15
lexu@mail.xidian.edu.cn 矢量场的通量与散度 • 矢量场的散度 – 为表征矢量 场内一点处 源的强弱而 引入散度的 概念! 15 V(M) 曲面内有 正源或负源 闭合曲面 通量正负 S 源在s内 分布情况及 一点处强弱 散度 全局特性 局部特性