§2 最短路问题 (继上页)把权数赋到图9-18中,得图9-19,再用Dijkstra算法求最短路。 59 41 30 23 22 16 16 17 7 18 22 31 30 41 图9-19 求解过程如下: (1)给定起始点V1标以(0,S)。 (2)这时={V},={2,g,V4,,V6}。孤集合为{(1,2),(1,),(1,V4,(1,),(1,6)},则 min(s12,S13,S14,S15,S16)=S12=16,给孤(V1,2)的终点2标以(16,1)。 (3)这时={V1,2h,J={3,V4,5,}。孤集合为{(V1,3).(1,V4),(W1,),(W1,V6),(2, g),(2,V4),(2,Vs),(W2,V6},有min(S13,S14,S15S16,S23,S24,S25S26)=S13=22,给孤(V1,V3)的终 点3标以(22,1)
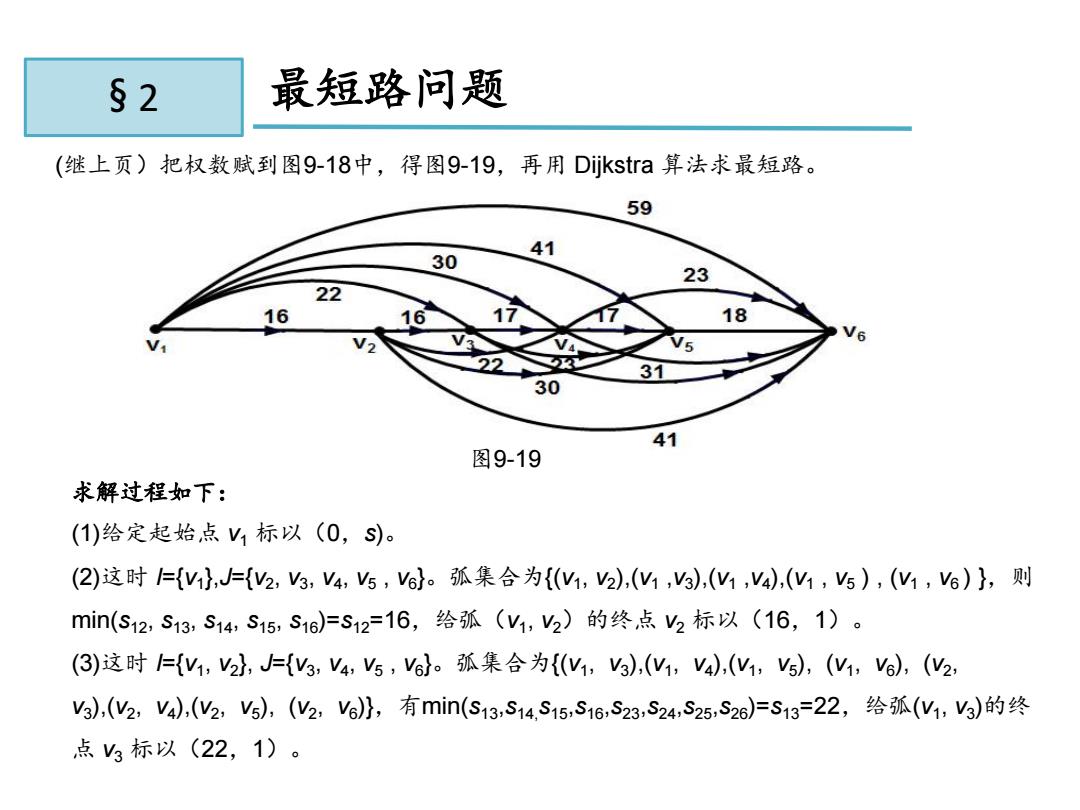
11.2 最短路问题 (继上页)把权数赋到图9-18中,得图9-19,再用 Dijkstra 算法求最短路。 求解过程如下: (1)给定起始点 v1 标以(0,s)。 (2)这时 I={v1 },J={v2 , v3 , v4 , v5 , v6 }。弧集合为{(v1 , v2 ),(v1 ,v3 ),(v1 ,v4 ),(v1 , v5 ) , (v1 , v6 ) },则 min(s12 , s13 , s14 , s15 , s16 )=s12=16,给弧(v1 , v2)的终点 v2 标以(16,1)。 (3)这时 I={v1 , v2 }, J={v3 , v4 , v5 , v6 }。弧集合为{(v1 , v3 ),(v1 , v4 ),(v1 , v5 ), (v1 , v6 ), (v2 , v3 ),(v2 , v4 ),(v2 , v5 ), (v2 , v6 )},有min(s13 ,s14,s15 ,s16 ,s23 ,s24 ,s25 ,s26 )=s13=22,给弧(v1 , v3 )的终 点 v3 标以(22,1)。 § 2 图9-19
§2 最短路问题 (4)这时={M1,3.g},J={V4.V5.V6}。则min(S14,S15.S16,S24.S25,S26,S34.S36,S36)=S14=30。给孤 (V1,V4)的终点V4标以(30,1)。 (5)这时={V1,V2,Vg,V4},J={yg,V6}。则min(S16,S16,S25,S26,S35,S36,S4s.S46)=S15=41。 给孤(V1,5)的终点5标以(41,1)。 (6)这时1={V1,V2,3,V4,5},J={V6}。则min(S16,S26,S36.S46,S56)=S36=S46=53。 给孤(g,%)和(v4,%)的终点6标以(53,3)和(53,4),最终得到图11-10,可知,V1到% 的距离是53,最短路径有两条:V1→3→%和V1→V4→V6。 59 41 30 23 22 16 2,30,1 16 1 18 V6 V V3 V423 V5(41,1 (53,3) (0,s) (16,1) 31 30 (53,4) 41 图9-10
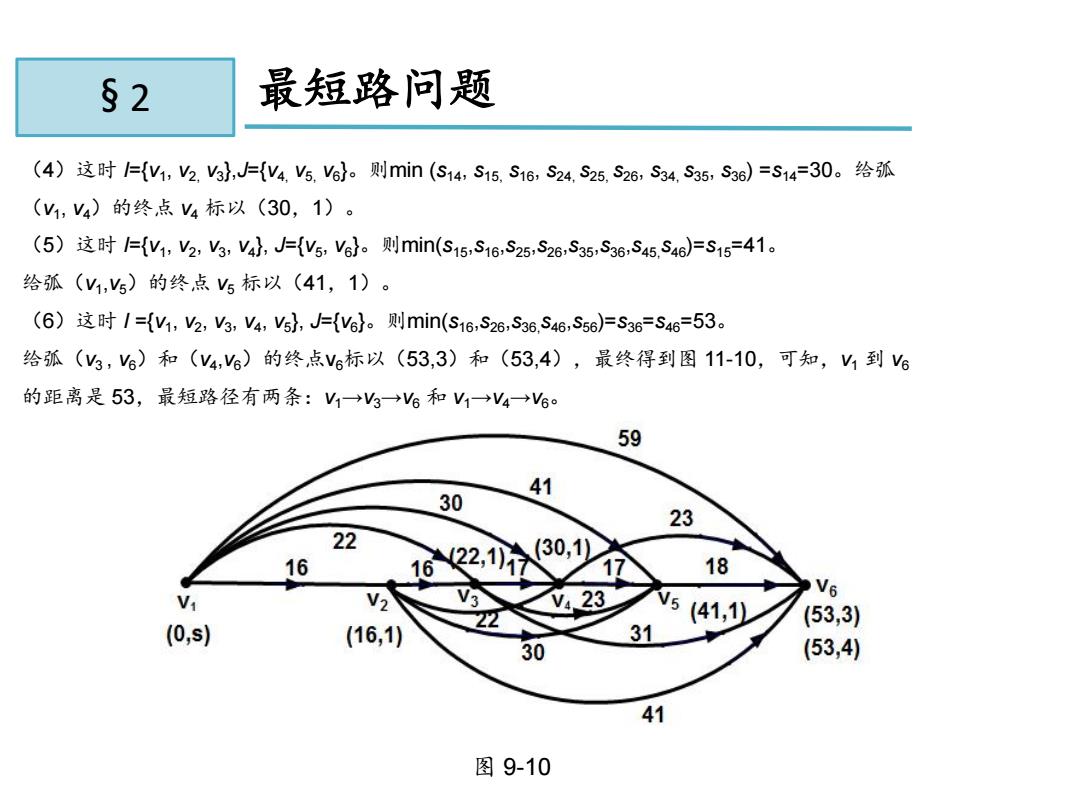
11.2 最短路问题 (4)这时 I={v1 , v2, v3 },J={v4, v5, v6 }。则min (s14 , s15, s16 , s24, s25, s26 , s34, s35 , s36 ) =s14=30。给弧 (v1 , v4)的终点 v4 标以(30,1)。 (5)这时 I={v1 , v2 , v3 , v4 }, J={v5 , v6 }。则min(s15 ,s16 ,s25 ,s26 ,s35 ,s36 ,s45,s46 )=s15=41。 给弧(v1 ,v5)的终点 v5 标以(41,1)。 (6)这时 I ={v1 , v2 , v3 , v4 , v5 }, J={v6 }。则min(s16 ,s26 ,s36,s46 ,s56 )=s36=s46=53。 给弧(v3 , v6)和(v4 ,v6)的终点v6标以(53,3)和(53,4),最终得到图 11-10,可知,v1 到 v6 的距离是 53,最短路径有两条:v1→v3→v6 和 v1→v4→v6。 图 9-10 § 2