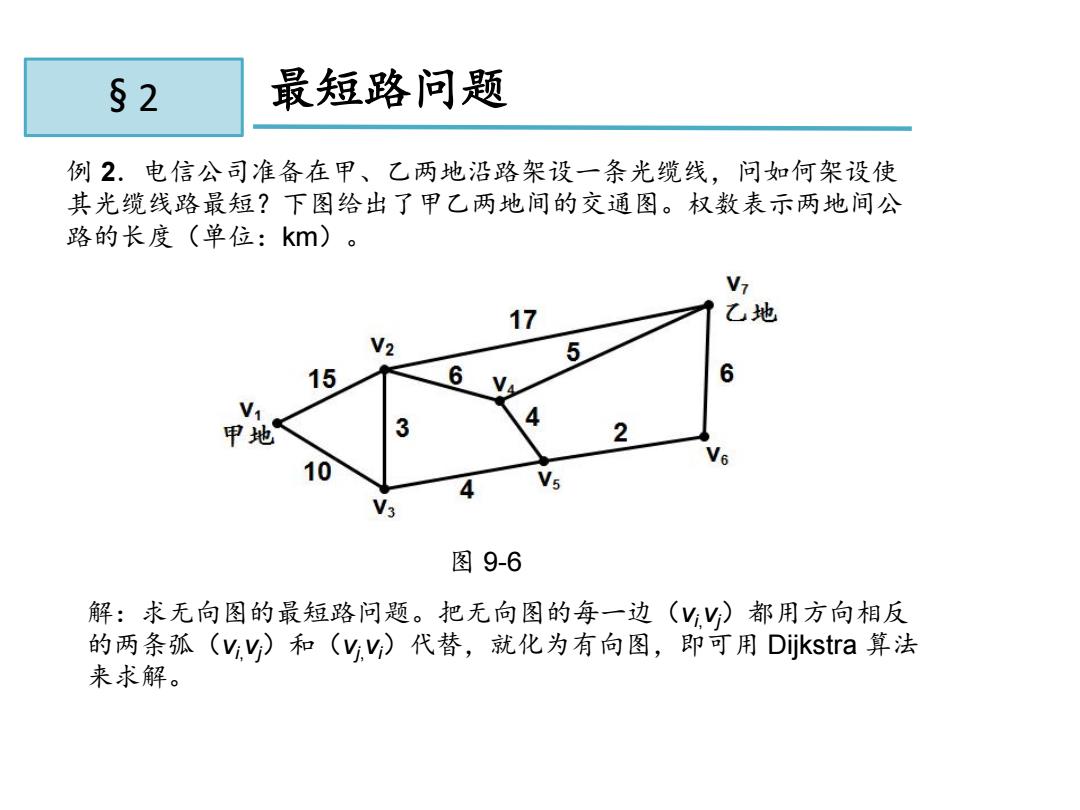
§2 最短路问题 例2.电信公司准备在甲、乙两地沿路架设一条光缆线,问如何架设使 其光缆线路最短?下图给出了甲乙两地间的交通图。权数表示两地间公 路的长度(单位:km)。 V7 17 乙地 V2 5 15 6 6 V 4 甲地 3 2 V6 10 图9-6 解:求无向图的最短路问题。把无向图的每一边(Y)都用方向相反 的两条孤(vy)和(yv)代替,就化为有向图,即可用Dijkstra算法 来求解
11.2 最短路问题 例 2.电信公司准备在甲、乙两地沿路架设一条光缆线,问如何架设使 其光缆线路最短?下图给出了甲乙两地间的交通图。权数表示两地间公 路的长度(单位:km)。 解:求无向图的最短路问题。把无向图的每一边(vi,vj)都用方向相反 的两条弧(vi,vj)和(vj,vi)代替,就化为有向图,即可用 Dijkstra 算法 来求解。 图 9-6 § 2

§2 最短路问题 例2求解过程如下 (1)给起始点V1,标号为(0,S)。 (2)={V},J={V2,3.V4,V5,V6,V}。边的集合为[V1,2][V1,V3l},则 S12=15,S13=10,min(S12,S13)=S13=10。给边[y1,3]中未标号点3标以(10,1)表示从 V1到的距离为10。 (3)这时={V1,Vg},={V2,V4,Vs,,}。边集合为V1,2],IV3,2l,[g,Vs},则有 min(S12,S32,S35)=S32=13。给边[g,2]中未标号点2标以(13,3)。 (4)这时={,g,2},J={v4,5,6,}.边集合为{g,sl,[2,V4,[2,},则有min (S35S24,S27)=S35=14。给边[V3.V6中未标号点5标以(14,3)。 (5)这时={V1,2,g,s},J={V4,6,}.边集合为{2,V4,[Vs,V4[V2,[Vs,6},则有 min(s24,S54,S27,S56=S56=16。给边[s.6l中未标号点6标以(16,5)。 (6)这时={V1.2,g,s,V6},J={V4,}。边集合为2.V4,[2,,[5,4,[V6,},则有 min(S24,S27,S54,S67=S5418。给边[V5,V4中未标号点V4标以(18,5)
11.2 最短路问题 例 2 求解过程如下 (1)给起始点 v1,标号为(0,s)。 (2)I={v1 },J={v2 ,v3,v4 ,v5 ,v6 ,v7 }。边的集合为{[v1 ,v2 ],[v1 ,v3 ]},则 s12=15,s13=10,min(s12 ,s13 )=s13=10。给边[v1 , v3 ]中未标号点 v3 标以(10,1)表示从 v1 到 v3 的距离为 10。 (3)这时 I={v1 ,v3 },J={v2 ,v4 ,v5 ,v6 ,v7 }。边集合为{[v1 , v2 ],[v3, v2 ], [v3 , v5 ]},则有 min(s12 ,s32 ,s35 )=s32=13。给边[v3 , v2 ]中未标号点 v2 标以(13,3)。 (4)这时 I={v1 ,v3 ,v2 }, J={v4 ,v5 ,v6 ,v7 }.边集合为{[v3 , v5 ],[v2 ,v4 ],[v2 ,v7 ]},则有min (s35 ,s24 ,s27)= s35=14。给边[v3, v5 ]中未标号点 v5 标以 (14,3)。 (5)这时 I={v1 ,v2 ,v3 ,v5 }, J={v4 ,v6 ,v7 }. 边集合为{[v2 ,v4 ],[v5 ,v4 ],[v2 ,v7 ],[v5 ,v6 ]}, 则有 min(s24 ,s54 ,s27 ,s56 )=s56=16。给边[v5,v6 ]中未标号点 v6 标以 (16,5)。 (6)这时 I={v1,v2 ,v3 ,v5 ,v6 }, J={v4 ,v7 }。边集合为{[v2,v4 ],[v2 ,v7 ],[v5 ,v4 ],[v6 ,v7 ]},则有 min (s24,s27 , s54 ,s67 ) =s54=18。给边[v5 ,v4 ]中未标号点 v4 标以 (18,5)。 § 2
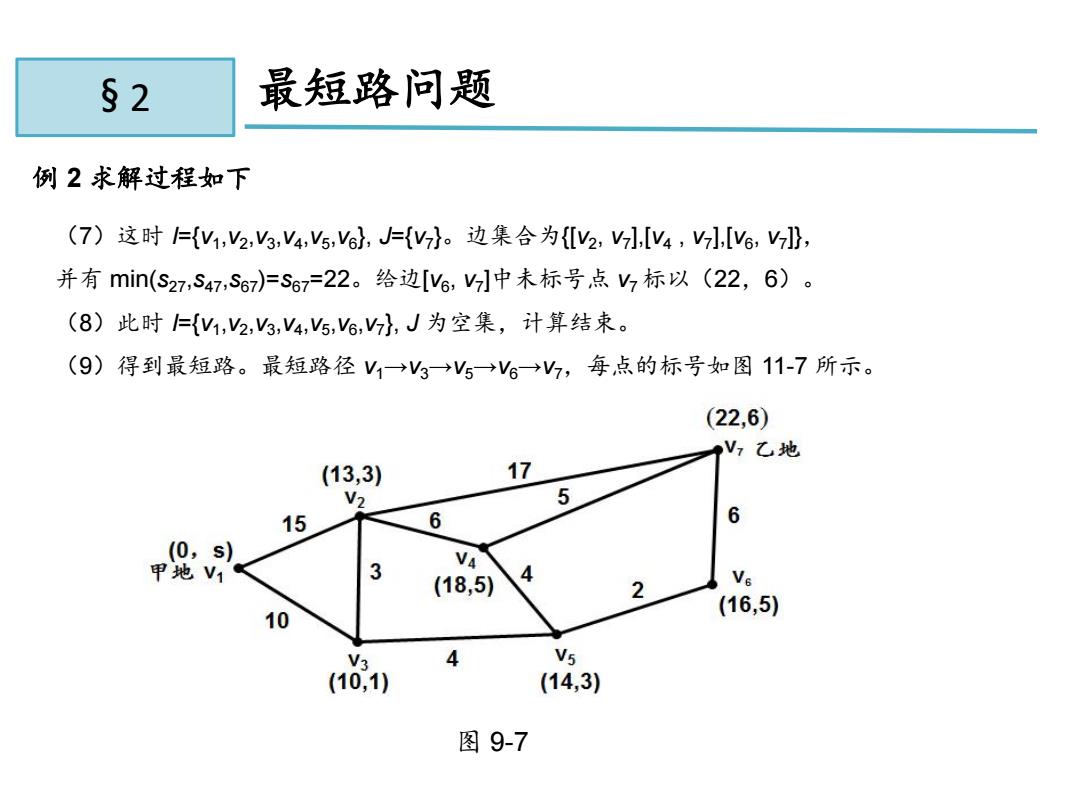
§2 最短路问题 例2求解过程如下 (7)这时={V1,2,3,V4,5,%},J={V}。边集合为{2,[V4,,[V%,}, 并有min(s27,S47,S67)=S67=22。给边[V6,J中未标号点,标以(22,6)。 (8)此时={V1,2,g,V4,5,6,},J为空集,计算结束。 (9)得到最短路。最短路径V1→3→Vs→V。→7,每点的标号如图11-7所示。 (22,6) V,乙地 (13,3) 17 V2 5 15 6 6 (0,s) 甲地V1 VA 3 (18,5) 4 Ve 2 10 (16,5) V? 4 V5 (10,1) (14,3) 图9-7
11.2 最短路问题 例 2 求解过程如下 (7)这时 I={v1 ,v2 ,v3 ,v4 ,v5 ,v6 }, J={v7 }。边集合为{[v2 , v7 ],[v4 , v7 ],[v6 , v7 ]}, 并有 min(s27 ,s47 ,s67 )=s67=22。给边[v6 , v7 ]中未标号点 v7 标以(22,6)。 (8)此时 I={v1 ,v2 ,v3 ,v4 ,v5 ,v6 ,v7 }, J 为空集,计算结束。 (9)得到最短路。最短路径 v1→v3→v5→v6→v7,每点的标号如图 11-7 所示。 图 9-7 § 2
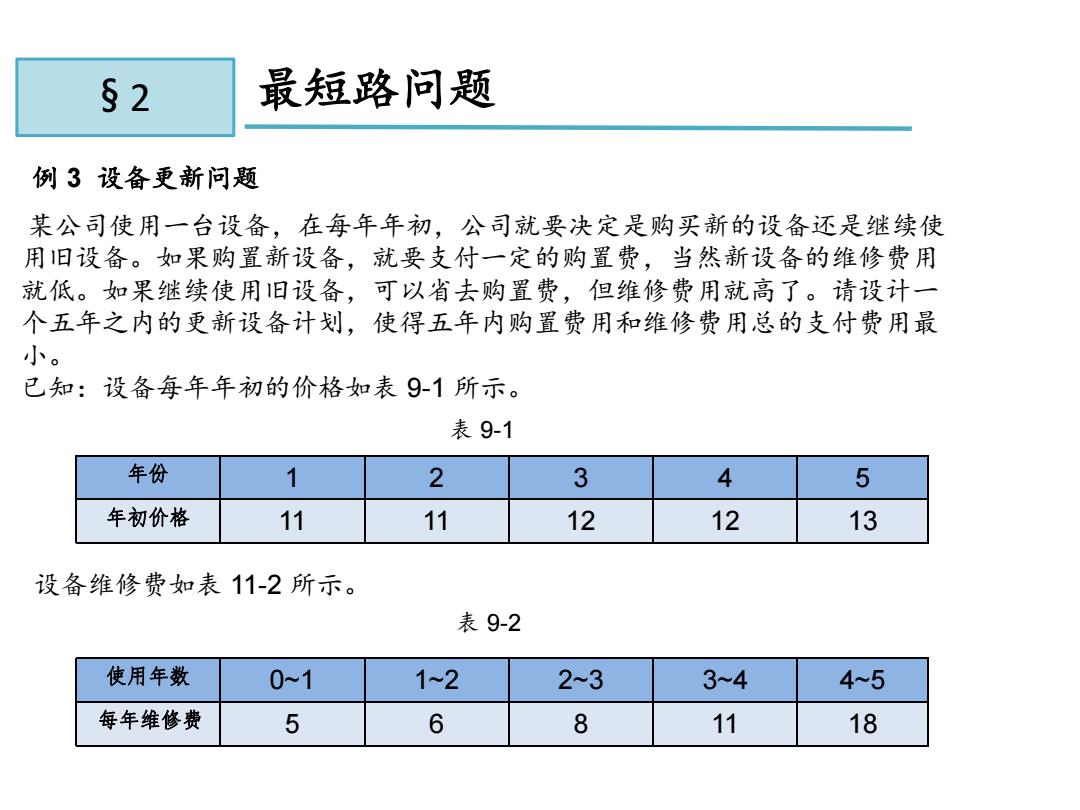
§2 最短路问题 例3设备更新问题 某公司使用一台设备,在每年年初,公司就要决定是购买新的设备还是继续使 用旧设备。如果购置新设备,就要支付一定的购置费,当然新设备的维修费用 就低。如果继续使用旧设备,可以省去购置费,但维修费用就高了。请设计一 个五年之内的更新设备计划,使得五年内购置费用和维修费用总的支付费用最 小。 已知:设备每年年初的价格如表9-1所示。 表9-1 年份 1 2 3 4 5 年初价格 11 11 12 12 13 设备维修费如表11-2所示。 表9-2 使用年数 0~1 12 2~3 3~4 4~5 每年维修费 5 6 8 11 18
11.2 最短路问题 例 3 设备更新问题 某公司使用一台设备,在每年年初,公司就要决定是购买新的设备还是继续使 用旧设备。如果购置新设备,就要支付一定的购置费,当然新设备的维修费用 就低。如果继续使用旧设备,可以省去购置费,但维修费用就高了。请设计一 个五年之内的更新设备计划,使得五年内购置费用和维修费用总的支付费用最 小。 已知:设备每年年初的价格如表 9-1 所示。 表 9-1 表 9-2 设备维修费如表 11-2 所示。 § 2 年份 1 2 3 4 5 年初价格 11 11 12 12 13 使用年数 0~1 1~2 2~3 3~4 4~5 每年维修费 5 6 8 11 18

§2 最短路问题 例3求解如下:将问题转化为最短路问题,如图9-8所示。 用V表示“第i年年初购进一台新设备”,孤(,y)表示第i年年初购进 的设备一直使用到第ⅰ年年初。 图9-8 把所有孤的权数计算如下表 1 2 3 4 5 6 16 22 30 41 59 2 16 22 30 41 0 17 23 31 4 17 23 5 18 6
11.2 最短路问题 例 3 求解如下:将问题转化为最短路问题,如图 9-8 所示。 用 vi 表示“第 i 年年初购进一台新设备” ,弧(vi,vj)表示第 i 年年初购进 的设备一直使用到第 j 年年初。 图 9-8 把所有弧的权数计算如下表 § 2 1 2 3 4 5 6 1 16 22 30 41 59 2 16 22 30 41 3 17 23 31 4 17 23 5 18 6