
第四章 相变 4.1平衡判据和稳定判据 4.2化学势 4.3相平衡条件 4.4相图和相变分类 4.5相图例子 4.6一阶相变 4.7亚稳平衡:过冷和过热现象 4.8 van der Waals流体的相变 4.9连续相变和临界现象 4.10 Landau二阶相变理论
第四章 相变 4.1 平衡判据和稳定判据 4.2 化学势 4.3 相平衡条件 4.4 相图和相变分类 4.5 相图例子 4.6 一阶相变 4.7 亚稳平衡:过冷和过热现象 4.8 van der Waals 流体的相变 4.9 连续相变和临界现象 4.10 Landau 二阶相变理论

引言 Q迄今为止,我们讨论的系统都是空间均匀的系统。系统内部 所有地方物质密度、能量密度都相同。 Q在一些特殊情况下,可能会自发出现空间不均匀的情况。不 同空间部分物质处于不同形态。比如冰水混合物:水和饱和 蒸汽共存。 Q热力学参数不同,物质可以处于不同的形态。 例如:常压下,低于零度水凝结成冰;高于一百度时为蒸汽: 介于二者为液体水 。为什么会改变形态?哪种形态更稳定?什么情况下可以多种 形态共存? 热力学平衡判据和稳定判据
引言 迄今为止,我们讨论的系统都是空间均匀的系统。系统内部 所有地方物质密度、能量密度都相同。 在一些特殊情况下,可能会自发出现空间不均匀的情况。不 同空间部分物质处于不同形态。比如冰水混合物;水和饱和 蒸汽共存。 热力学参数不同,物质可以处于不同的形态。 例如:常压下,低于零度水凝结成冰;高于一百度时为蒸汽; 介于二者为液体水 为什么会改变形态?哪种形态更稳定?什么情况下可以多种 形态共存? ☞ 热力学平衡判据和稳定判据
4.1平衡判据和稳定判据 力学平衡判据 Q原始参量判据:总力=0,总力矩=0, Q高级参量:势能(或者总能量)最/极值点· 一二者等价,但是对于复杂系统数学上可能更加简单 多个条件合并为一个
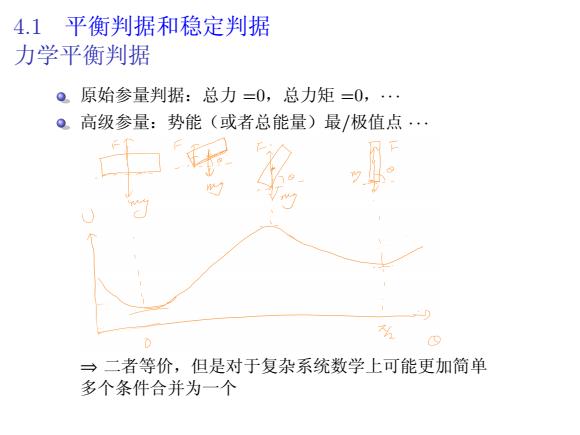
4.1 平衡判据和稳定判据 力学平衡判据 原始参量判据:总力 =0,总力矩 =0,· · · 高级参量:势能(或者总能量)最/极值点 · · · ⇒ 二者等价,但是对于复杂系统数学上可能更加简单 多个条件合并为一个

平衡判据:平衡分类 中 露稳定平衡:能量最低,即使有很大的扰动也可恢复 能量一阶导数为零,二阶导数大于零 G】 不稳平衡:能量极大,无穷小扰动即破坏 能量一阶导数为零,二阶导数小于零 ⑧亚稳平衡:能量极小但非最小,小扰动稳定,大扰动不稳 能量一阶导数为零,二阶导数大于零 能量一阶导数、二阶导数是都为零?⑧大的涨落
平衡判据:平衡分类 ☞ 稳定平衡:能量最低,即使有很大的扰动也可恢复 能量一阶导数为零,二阶导数大于零 ☞ 不稳平衡:能量极大,无穷小扰动即破坏 能量一阶导数为零,二阶导数小于零 ☞ 亚稳平衡:能量极小但非最小,小扰动稳定,大扰动不稳 能量一阶导数为零,二阶导数大于零 ☞ 能量一阶导数、二阶导数是都为零?☞ 大的涨落

热力学系统的平衡判据 e 原始参量判据 力学平衡:压强均匀: 热学平衡:温度均匀: 化学平衡:密度均匀 Q高级参量判据? 霉类似力学判据,可以利用热力学第二定律从特性函数的极 值条件判断平衡和稳定 热力学系统里自发有小扰动(涨落),因此只有稳定平衡 和亚稳平衡两类 大涨落情况?
热力学系统的平衡判据 原始参量判据 力学平衡:压强均匀; 热学平衡:温度均匀; 化学平衡:密度均匀 · · · 高级参量判据? ☞类似力学判据,可以利用热力学第二定律从特性函数的极 值条件判断平衡和稳定 ☞热力学系统里自发有小扰动(涨落),因此只有稳定平衡 和亚稳平衡两类 ☞大涨落情况?