第10章土城稳定性分析 第1节概述 土坡是具有倾斜表面的土体,由自然地质作用所形成的土坡, 如山坡、江河的岸坡等,称为天然土坡。由人工开挖或回填而形成 的土坡,如基坑、渠道、土坝、路堤等的边坡,则称为人工土坡。 土体自重以及渗透力 坡肩 坡顶 等在坡体内引起剪应力, 如果剪应力大于土的抗剪 坡面 强度,就要产生剪切破坏, 一部分土体相对于另一部 坡底 坡角 分土体滑动的现象,称为 坡趾 滑坡或塌方。 土坡各部位的名称 土质学与土力学 33-1 吉林大学建设工程学院
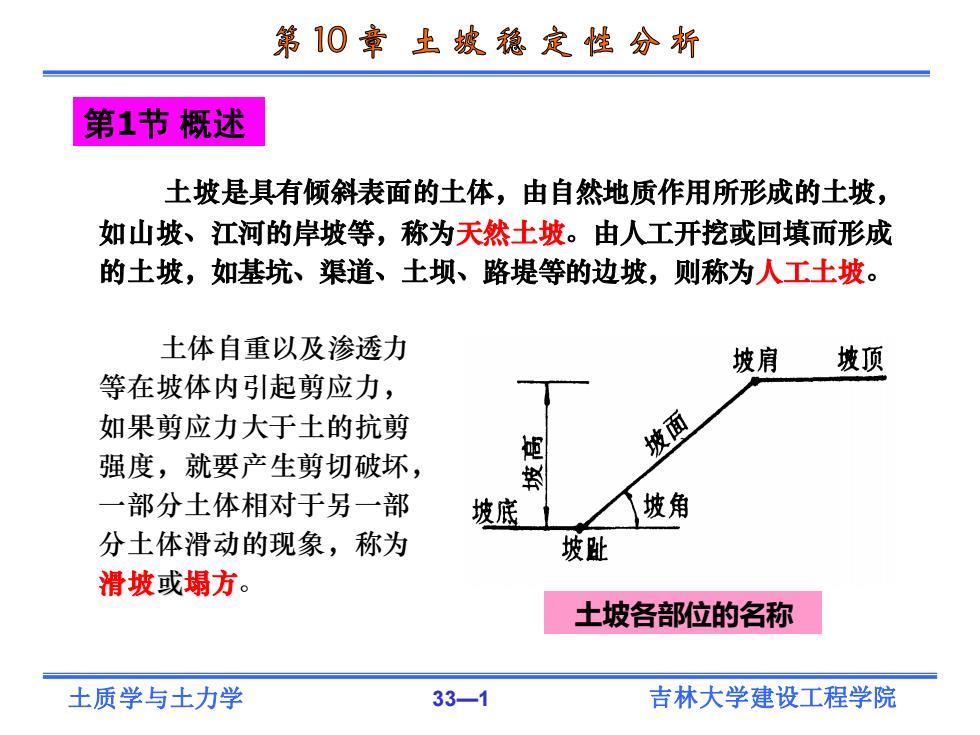
土质学与土力学 33—1 吉林大学建设工程学院 土坡是具有倾斜表面的土体,由自然地质作用所形成的土坡, 如山坡、江河的岸坡等,称为天然土坡。由人工开挖或回填而形成 的土坡,如基坑、渠道、土坝、路堤等的边坡,则称为人工土坡。 土体自重以及渗透力 等在坡体内引起剪应力, 如果剪应力大于土的抗剪 强度,就要产生剪切破坏, 一部分土体相对于另一部 分土体滑动的现象,称为 滑坡或塌方。 第1节 概述 土坡各部位的名称
第10章土城稳定性分析 影响土坡稳定性的因素 边坡坡角,越小越安全,但不经济 坡高,坡高越大越不安全 土的性质,如重度,凝聚力,内摩擦角 地下水的渗透力,渗透力作用方向与滑动方 向相反则安全,否则则危险 震动作用的影响 人类活动和生态环境的影响 土质学与土力学 33-2 吉林大学建设工程学院
土质学与土力学 33—2 吉林大学建设工程学院 影响土坡稳定性的因素 边坡坡角,越小越安全,但不经济 坡高,坡高越大越不安全 土的性质,如重度,凝聚力,内摩擦角 地下水的渗透力,渗透力作用方向与滑动方 向相反则安全,否则则危险 震动作用的影响 人类活动和生态环境的影响
第10章土城稳定性分析 通常不考虑滑动土体两端阻力的影响,将土坡稳定分析简化 为平面应变问题。而起滑动面可简化为三种,即直线形,圆弧形 和复合形。 (a) (b) (c) 土坡滑动面形状 (a)圆弧形;(b)直线形;(c)复合形 土质学与土力学 33-3 吉林大学建设工程学院
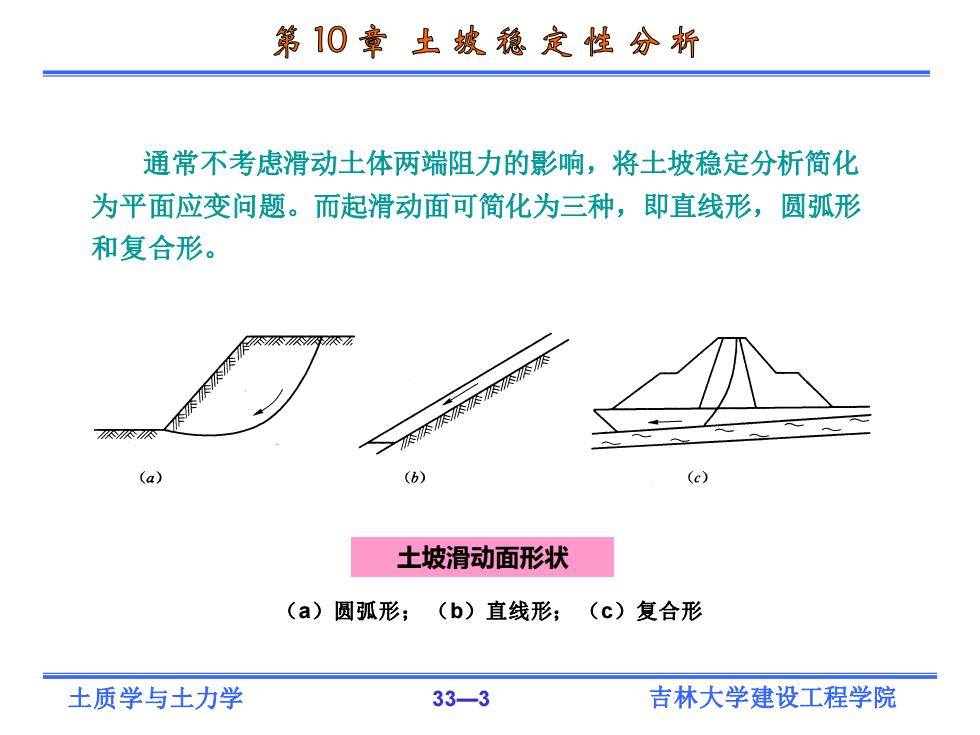
土质学与土力学 33—3 吉林大学建设工程学院 土坡滑动面形状 (a)圆弧形; (b)直线形; (c)复合形 通常不考虑滑动土体两端阻力的影响,将土坡稳定分析简化 为平面应变问题。而起滑动面可简化为三种,即直线形,圆弧形 和复合形

第10章土城稳定性分析 第2节无粘性土土坡的稳定分析 由砂、卵石、风化砾石等堆筑的土坡称无粘性土坡 稳定条件:只要坡面上的土颗粒在重力作用下能够保持稳定,整 个土坡就处于稳定状态。 稳定性分析 砂堆 从坡面上取一士体单元。土体重量为W。 (a (b) 滑动力T=W sina 正压力N=W cosa 土体的稳定安全系数F为: 抗滑力T=W tan=Wcosatan p一土的内摩擦角;α一土坡的坡角 F,= W cosa tan o tanp 当F=1时,心=0,α称为天然休止角。 T Wsin a tan a 土质学与土力学 33-4 吉林大学建设工程学院
土质学与土力学 33—4 吉林大学建设工程学院 由砂、卵石、风化砾石等堆筑的土坡称无粘性土坡 稳定条件:只要坡面上的土颗粒在重力作用下能够保持稳定,整 个土坡就处于稳定状态。 稳定性分析 从坡面上取一土体单元。土体重量为W。 滑动力 T=W sin 正压力 N=W cos 抗滑力 Tf=N tan =Wcostan — 土的内摩擦角; — 土坡的坡角 当Fs =1时, =, 称为天然休止角。 土体的稳定安全系数Fs为: tan tan sin cos tan = = = W W T T F f s 第2节 无粘性土土坡的稳定分析

第10章土城稳定性分析 第3节粘性土土坡的稳定分析 粘性土由于粘聚力的存在,粘性土坡不像无粘性土坡一样仅沿坡面表面 滑动。均质粘性土坡的滑动面近似于圆柱面,在工程设计中常假定滑动面为 圆弧面。建立在这一假定基础上的土坡稳定分析方法称为瑞典圆弧滑动法。 瑞典圆狐滑动法 原理:均质的粘性土坡失去稳定是由于滑动土体绕圆心发生转动。把 滑动土体当成一个刚体,滑动土体的重量W,将使土体绕圆心O旋转, 滑动力矩为M、=W。对于饱和粘土,在不排水条件下,p=0,滑动 面AC上粘聚力产生抗滑力矩C·L·R 土质学与土力学 33-5 吉林大学建设工程学院
土质学与土力学 33—5 吉林大学建设工程学院 粘性土由于粘聚力的存在,粘性土坡不像无粘性土坡一样仅沿坡面表面 滑动。均质粘性土坡的滑动面近似于圆柱面,在工程设计中常假定滑动面为 圆弧面。建立在这一假定基础上的土坡稳定分析方法称为瑞典圆弧滑动法。 原理:均质的粘性土坡失去稳定是由于滑动土体绕圆心发生转动。把 滑动土体当成一个刚体,滑动土体的重量W,将使土体绕圆心O旋转, 滑动力矩为Ms =Wx。对于饱和粘土,在不排水条件下,u=0,滑动 面AC上粘聚力产生抗滑力矩 cu LR 第3节 粘性土土坡的稳定分析 瑞典圆弧滑动法