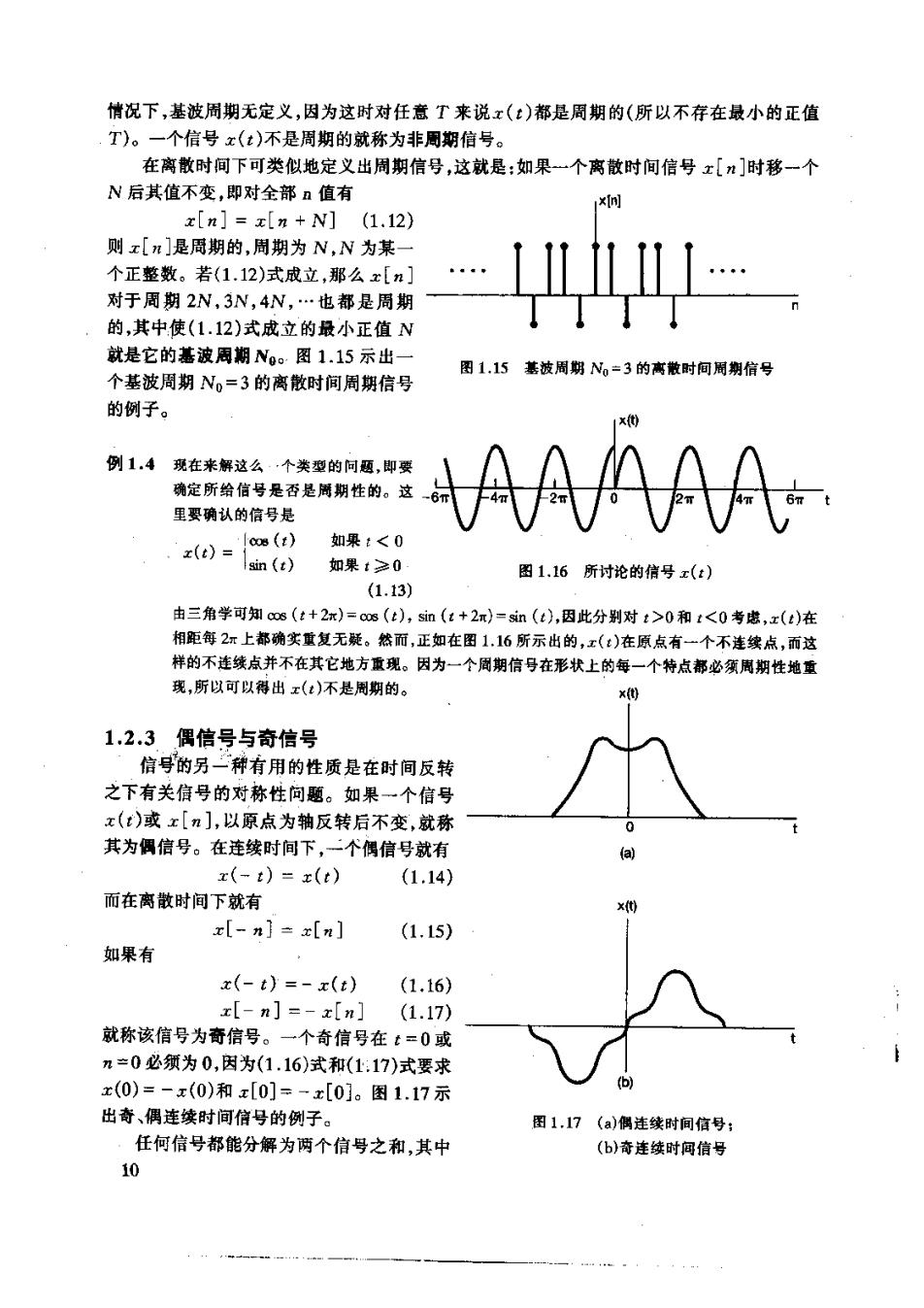
情况下,基波周期无定义,因为这时对任意T来说x(:)都是周期的(所以不存在最小的正值 T)。一个信号x(:)不是周期的就称为非周期信号。 在离散时间下可类似地定义出周期信号,这就是:如果一个离散时间信号x[n]时移一个 N后其值不变,即对全部n值有 x[n]=x[n+N](1.12) 则x[m]是周期的,周期为N,N为某 个正整数。若(1.12)式成立,那么x[n] 对于周期2N,3N,4N,.也都是周期 的,其中使(1.12)式成立的最小正值N 就是它的基波周期N0。图1.15示出 图1.15基被周期N。=3的离散时何周期信号 个基波周期N0=3的离散时间周期信号 的例子。 例1.4现在来解这么,个类型的问题,即安 确定所给信号是否是周期性的。 这 里要确认的信号是 NAAAA x(t)= 如果:<0 如果t≥0 图1.16所讨论的信号x(t) (1.13) 由三角学可知cs(t+2x)=os(),s血(+2)=sn(d),因此分别对:>0和<0考感,x()在 相距每2上都确实重复无疑。 然而 正如在图1.16所示出的,x()在原点有一个不连续点,而这 样的不连线点 不在其它地方重现。因为一个园期信号在形状上的每一个特点都必衡周期性地重 现,所以可以得出x()不是周期的。 1.2.3偶信号与奇信号 信号的另二种有用的性质是在时间反转 之下有关信号的对称性问题。如果一个信号 z()或x[n],以原点为轴反转后不变,就称 其为偶信号。在连续时间下,二个偶信号就有 x(-t)=x(t) (1.14) 而在离散时间下就有 x[-n]÷x[t] (1.15) 如果有 x(-t)=-x(t) (1.16) x[-n]=-x[n](1.17) 就称该信号为奇信号。一个奇信号在:=0或 n=0必须为0,因为(1.16)式和(1:17)式要求 x(0)=-x(0)和x[0]=-x[0]。图1.17示 出奇、偶连续时间信号的例子。 图1.17(a)侧连续时间信号: 任何信号都能分解为两个信号之和,其中 (6)奇连续时闻信号 10

之一为偶信号,另一个为奇信号。为此考 虑下列信号 x(t)川=[x(t)+x(-t] (1.18) x(t)川=[x(t)-z(-t)] (1.19 6{x(t),似x(:)1分别称为x(t)的偶 部和奇部。很简单地就可确认偶部是偶 a时图 信号,而奇部是奇信号,且x(t)就是两者 之和。在离傲时间下上球结论也完会成 立。图1.18示出一个离散时间信号奇偶 .t 分解的例子。 1.3指数信号与正弦信号 这一节和下一节要介绍几个基本的 连续时间和离散时间信号。这样做不仅 仅是因为这些信号经常出现,更重要的是 它们可以用作基本的信号构造单元来构 成其它许多信号。 1.3.1连续时间复指数信号与正弦 图1.18离散时间信号奇偶分解的例子 信号 连续时间复指数信号具有如下形式: r(t)=Ce (1.20) 式中C和口一般为复数。根据这些参数值的不同,复指数信号可有几种不同的特征。 实指数信号 如图1.19所示,若C和a都是实数(这时x(:)就称为实指数信号】,就有两种类型的特 性。若a是正实数,那么x(t)随t的增加而指数增长。这种类型的信号可以用来描述原子燥 炸或复杂化学反应中的链锁反应等很多不同的物理过程。若a是负实数,则x(:)随:的增加 而指数衰诚。这类信号也可用来描述诸如放射性衰变、RC电路以及有阻尼的机械系统的响 应等范围 广泛的各种现象。特别是,如同在习题2.61和2.62中所指出的,图1.1电路和图 1.2中的汽车,它们的自然响应都是指数在减的。对于a=0,x(t)就为一常数 周期复指数和正弦信号 第二种重要的复指数信号是将α限制为纯虚数,特别是考虑如下信号: 11
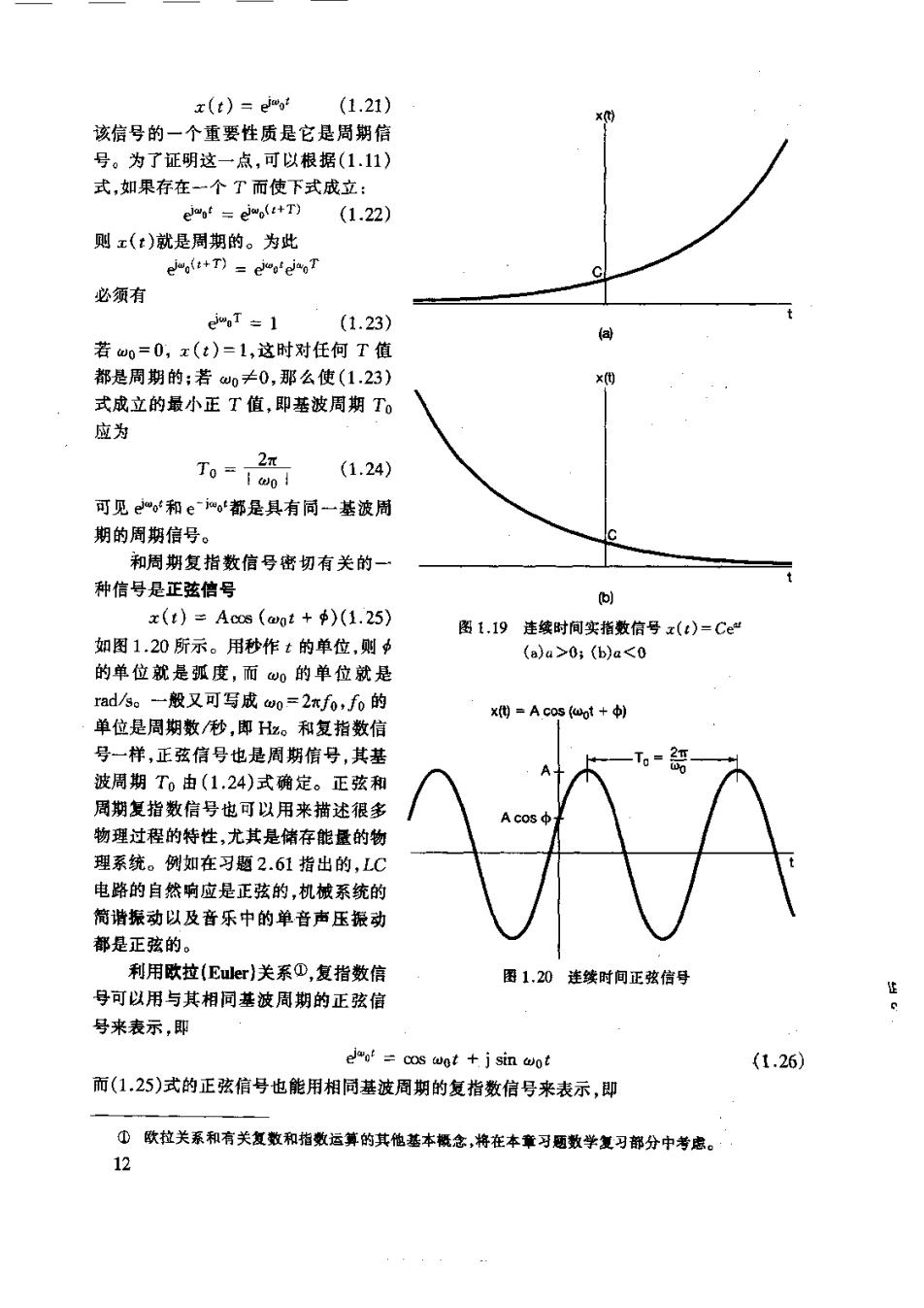
z(t)=em, (1.21) 该信号的一个重要性质是它是周期信 号。为了证明这一点,可以根据(1.11) 式,如果存在一个T而使下式成立: ju。‘=cjwo4+T) (1.22) 则x()就是周期的。为此 e+T)=cg'cisoT 必须有 (1.23) 若o=0,x(t)=1,这时对任何T值 都是周期的:若0≠0,那么使(1.23) x( 式成立的最小正T值,即基被周期T0 应为 2x T0=1 (1.24) 可见e,和emo'都是具有同一基波周 期的周期信号。 和周期复指数信号密切有关的一 种信号是正兹倍号 bl x(t)=Acs(aot+)(1.25) 图1.19连续时间实指数信号x()=Ce 如图1.20所示。用秒作t的单位.则 Ba>0b)a<0 的单位就是弧度,而0的单位就是 rads。一般又可写成0=2xf0,f0的 单位是周期数秒,即Hz。和复指数信 x用=Acos0l+ 号一样,正弦信号也是周期信号,其基 一T=3 波周期T)由(1.24)式确定。正弦和 周期复指数信号也可以用来描述很多 物理过程的特性,尤其是储存能量的物 理系统。例如在习题2.61指出的,LC 电路的自然响应是正弦的,机械系统的 简谐振动以及音乐中的单音声压振动 都是正弦的。 利用欧拉(Eer)关系①,复指数信 图1,20连续时间正弦信号 号可以用与其相同基波周期的正弦信 号来表示,即 =cos wot +j sin (1.26 而(1.25)式的正弦信号也能用相同基波周期的复指数信号来表示,即 ①欧拉关系和有关复数 指数运算的其他基本凝念,将在本章习题数学复习都分中考虑
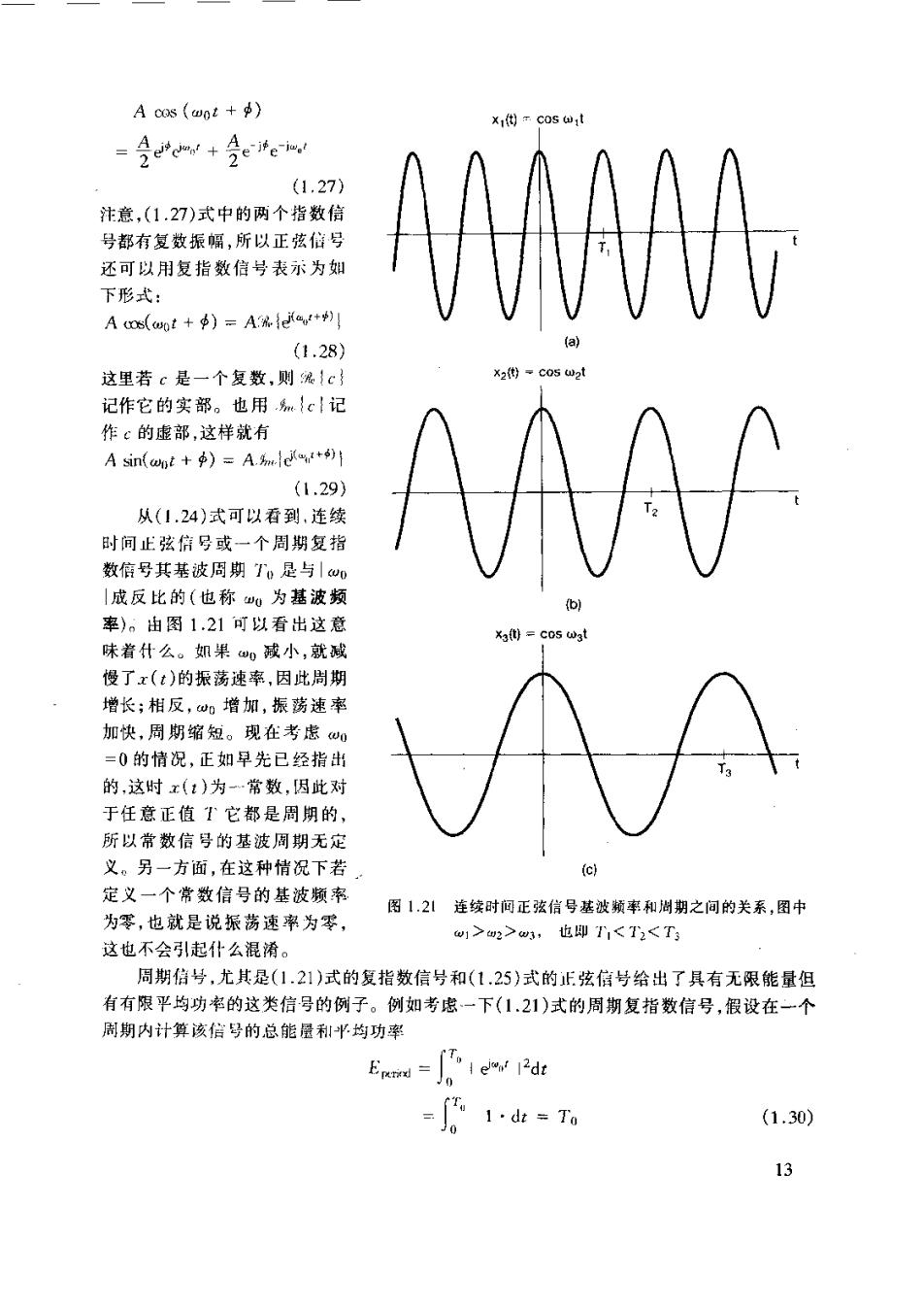
A oos (wnt+) oy te (1.27) 汁章(127)式中的两个指数倍 号都有复数振幅,所以正弦信号 还可以用复指数信号表示:为如 下形式: A cos(wot+=A (1.28) 这里若c是一个复数,则%1c 记作它的实部。也用{c记 作的部这样就有 A sin(apt=A. (1.29》 从(1.24)式可以看到,连续 时间正弦信号或一个周期复指 数信号其基波周期T是与引w, 成反比的(也称为基波频 率)。由图1.21可以看出这意 味着什么。如果酸小,就 慢了x()的振荡速率,因此周期 增长;相反,增加,振荡速率 加快,周期缩短。现在考虑 =0的情况,正如早先已经指出 的,这时x(:)为常数,因此对 于任意正值T它都是周期的, 所以常数信号的基波周期无定 义。另一方面,在这种情况下若 定义一个常数信号的基波频率 为零,也就是说振荡速率为零, 图1.21连续时闷正弦信号基波顿率和尚期之间的关系,图中 1>2>w3,也即T<T2<T3 这也不会引起什么混滑 周期信号,尤其是(1.21)式的复指数信号和(1.25》式的正弦信号给出了具有无限能量但 有有限平均功的这类信号的例子。例如考虑一下(1.21)式的周期复指数信号,假设在一个 周期内计算该信号的总能层和半均功率 = 1·d=T (1.30) 13

Pam=六Eou=1 (1.31) 因为随着:从一∞到+∞,有无穷多个周期,所以在整个全部时间内积分其总能量就是无限 大,该信号的每个周期都完全是一样的,因为在每个周期内信号的平均功率等于1,所以在多 个周期上平均也总是得到1的平均功率。这就是说,周期复指数信号具有有限平均功率等于 p=1w2a=1 (1.32) 在习题1.3中还给出了另外儿个有关计算周期和非周期信号能量和功率的例子。 周期复指数信号在讨论信号与系统的大部分问题中都起着十分重要的作用,部分原因是 由于对许多其它信号来说,它们可用作极其有用的信号基本构造单元。同时,一组成谐波关系 的复指数信母也是很有用的:也就是周蝴复指数信母的售合该衡合内的全部信县都是周期 的,且有一个公共周期T。对一个复指数信号“要成为具有周期为T。的周期信号的必要条 件是 eo=1 (1.33) 这就意味着wT0是2π的倍数,即 WTo=2xk, =0,±1,±2,. (1.34) 由此,若定义 = (1.35) 可以得出,为满足(1.34)式,w必须是0的整倍数。这就是说,一个成谐被关系的复指数信号 的集合就是一组其基波频率是某一正频率的整倍数的周期复指数信号,即 克(t)=co',k=0,±1,±2,. (1.36) 若k=0,4(:)就是一个带数;面对任何其它的表值,(:)是周期的,其基波颜率为如0,基 波周期为 (1.37) 因为在任何长度为T。的时间间隔内,恰好通过了|个基波周期,所以第次谐波:(:)对 T。来说仍然是周期的。 这里用的术语“谐被”与在音乐中所用的意思是相同的,即由声压振动得到的各种音调其 频率都是某一基波颗率的整倍数。例如,小提琴上的一根弦的振动模式就能够当作一组成谐 波关系的周期指数信号的加权和。在第3章将看到,利用(1,36)式成谐波关系的信号作为基 本构造单元可以构成各种各样的周期信号。 例1.5 有时希塑把两个复指数的和化成单一的复指数和单一的正弦函数的乘积来表示。例如我们要想画 出下面信号的模 x(t)=e+ei (1.38) 为此可以首先将(138)试右边的两个复指数进行因式分解,其具体作法是将右边和式的两个指数 中的须率求得它们的平均值,然后作为公共因 子提出来,为此可得 (2)e(e-s+e.s) (1.39) 根据厥拉关系,上式可写成 14