
其平均功率为 g0业=a+R) (1.3) 相类似,对于图1.2中的汽车,由于摩擦所耗散的瞬时功率是p(t)=m(t),然后就可以按 (1.2)式和(1.3)式来定义在其一段时间内的总能量和平均功率。 利用这些简单的实际例子作为楔子,就可以对任何连续时间信号x(:)或离散时间信号 x[:]采用类似的功率和能量的术语。然面,不久将会看到,往往把信号看作具有复数值更为 方便,这时在t1≤t≤t2内的总能量对于一个连缕时间信号x(t)来说就定义为 作1x)2d (1.4) 这里|x记作x(可能为复散)的模。其平均功率将(1,4)式用2~1除就可得到。相类似,在 1≤n≤n2内的离散时间信号x[n]的总能量就是 克![]2 (1.5) 将其除以”2一”1+1就得到在该区间内的平均功率。要牢记的是,这里所用的“功率”和“能 量”与(1.4)式和(1.5)式中的量是否与真正的物理量相联系是无关的①。尽管如此,我们仍发 现采用这些术语在一般意义上是方便的。 再者,在很多系统中关心的是信号在一个无穷区间内(即-∞<t<+∞或-0<n<+ ∞)的功率和能量,在这些情况下,将总能量定义成按(1,4)式和(1.5)式,将其区间趋于无穷的 极限来考虑,在连续时间情况下就是 Ew△,lxe)at-∫广1xe)dt (1.6) 而在离散时间情况下就是 E金照2n]2=艺1zmJp (1.7) 注意,对某些信号(1.6)式的积分,或(1.7)式的求和可能不收敛,譬如若x(t)或x[n]在全部 时间内都为某-一非零的常数值就是这样。这样的信号具有无限的能量,而E。<∞的信号具 有有限的能量 关于在无限区间内的平均功率,可以类似的方式分别定义为 P.()idt (1.8) 和 [] P4m2N+1,之 (1.9) 利用这些定义就可以区分三种重要的信号。其中之一是信号具有有限的总能量,即E。<∞。 这种信号的平均功率必须为零,因为在连续时间情况下,由(1.8)式可看出 器特整製提器黄输器器
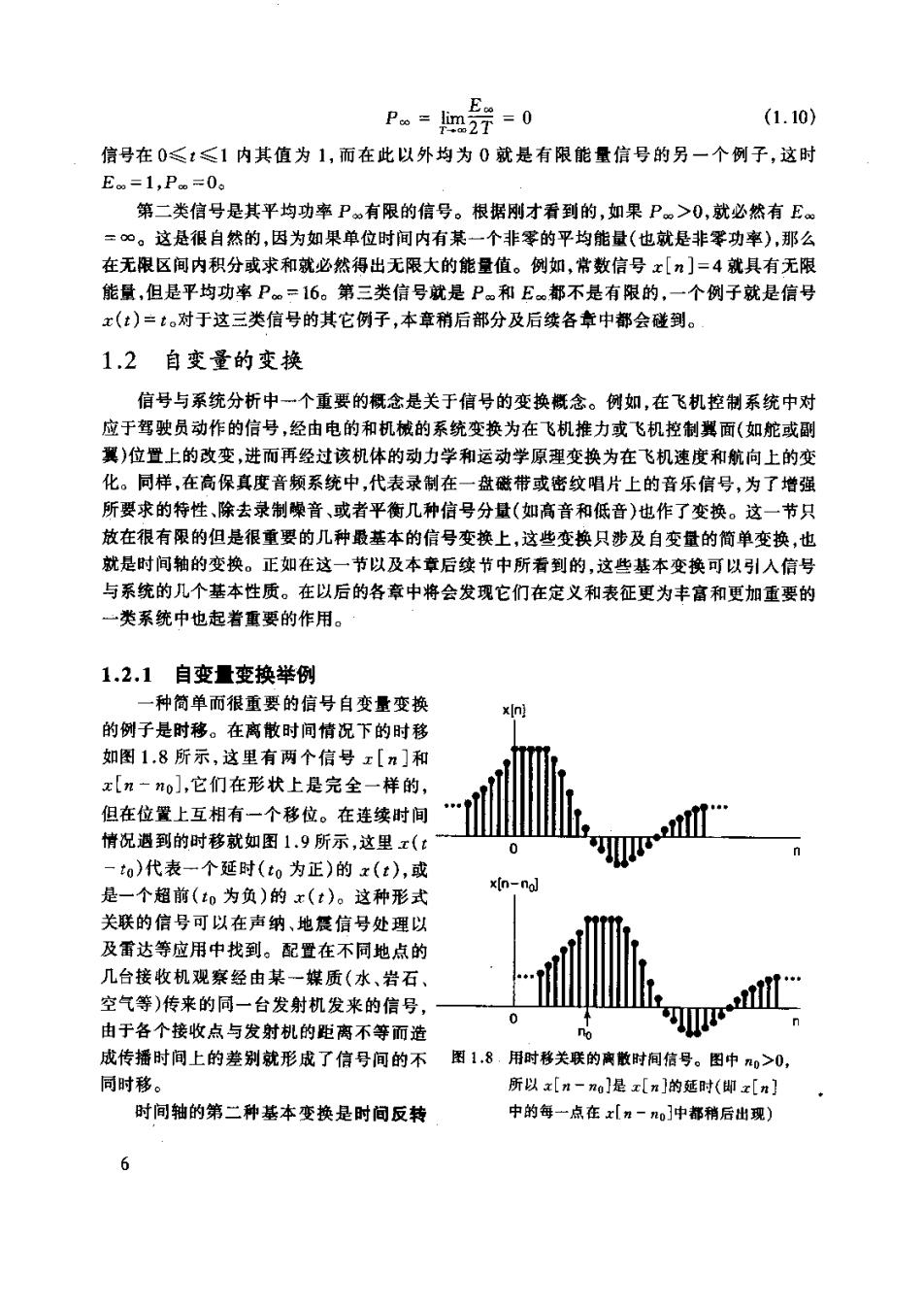
Pm=m2器=0 (1.10) 信号在0≤:≤1内其值为1,而在此以外均为0就是有限能量信号的另一个例子,这时 Em=1,Po=0。 第二类信号是其平均功率P有限的信号。根据刚才看到的,如果P>0,就必然有E =©。这是很自然的,因为如果单位时间内有某一个非零的平均能量(也就是非零功率),那么 在无限区间内积分或求和就必然得出无限大的能量值。例如,常数信号x[n]=4就具有无限 能质,但是平均功率P=16。第三类信号就是Pm和E都不是有限的,一个例子就是信号 x(t)=:。对于这三类信号的其它例子,本章稍后部分及后续各幸中都会碰到。 1.2 自变量的变换 信号与系统分析中一个重要的概念是关于信号的变换概念。例如,在飞机控制系统中对 应于驾驶员动作的信号,经由电的和机械的系统变换为在飞机推力或飞机控制翼面(如舵或副 翼)位置上的改变,进而再经过该机体的动力学和运动学原理变换为在飞机速度和航向上的变 化。同样,在高保真度音系统中,代表录制在一盘磁带或密纹唱片上的音乐信号,为了增强 所要求的特性、除去录制噪音、或者平衡几种信号分量(如高音和低音)也作了变换。这一节只 放在很有限的但是很重要的几种最基本的信号变换上,这些变换只莎及自变量的简单变换,也 就是时间轴的变换。正如在这一节以及本章后续节中所看到的,这些基本变换可以引入信号 与系统的儿个基本性质。在以后的各章中将会发现它们在定义和表征更为丰富和更加重要的 类系统中也起重要的作用。 1.2.1自变量变换举例 一种简单而很重要的信号自变量变换 的例子是时移。在离散时间情况下的时移 如图1.8所示,这里有两个信号x[n]和 x[n一no],它们在形状上是完全一样的 但在位置上互相有一个移位。在连续时间 情况遇到的时移就如图1.9所示,这里x(: -t0)代表一个延时(to为正)的x(t),或 是一个超前(o为负)的x(t)。这种形式 关联的信号可以在声纳、地震信号处理以 及雷达等应用中找到。配置在不同地点的 几台接收机观察经由某一煤质(水、岩石 空气等)传来的同一台发射机发来的信号 由于各个接收点与发射机的距离不等而造 成传播时间上的差别就形成了信号间的不 图1.8.用时移关联的离散时同佑号。图中0>0 同时移。 所以x[n-a是x[n]的延时(即x[n] 时间轴的第二种基本变换是时间反转 中的每一点在x[m一]中都稍后出现) 6

(time reversal)。例如在图1.10中,x[-#]就是将x[n]以n=0为轴反转而得到的。同样图 1.11中,x(-t)也是从信号x(:)以=0为轴反转而得的。这样,如果x(:)是代表一盘录制 的声音磁带的话,那么x(一)就代表同样一盘磁带倒过来放(即从末尾向前倒放)的结果。第 三种基本变换是时间尺度变换(time scaling)。在图1.l2中示出了x(t),x(2t)和x(t2)三 个信号,这三个信号是与自变量的线性尺度变换联系者的。倘若我们再一次把x(:)想象为 盘录音磁带的话,那么x(2:)将是这盘磁带以两倍的速度放音的结果,而x(:2)则代表原磁 带将放音速度降低一半。 1.9用时移关联的连续时间信号。图 中o<0,所以x(t-t)就是- (b) 超前的x(:)(即在x(:)中的每 点在1-)中都提前出) 图1.10(a)离敢时间信号x: 《b)x[#]以#-0为轴反转后的x[一n] 图1.1(a)连续时间信号x(t)小: 图1.12用时间尺度变换关联的连续时间信号 (b)x()以t=0为轴反转后的x(-)
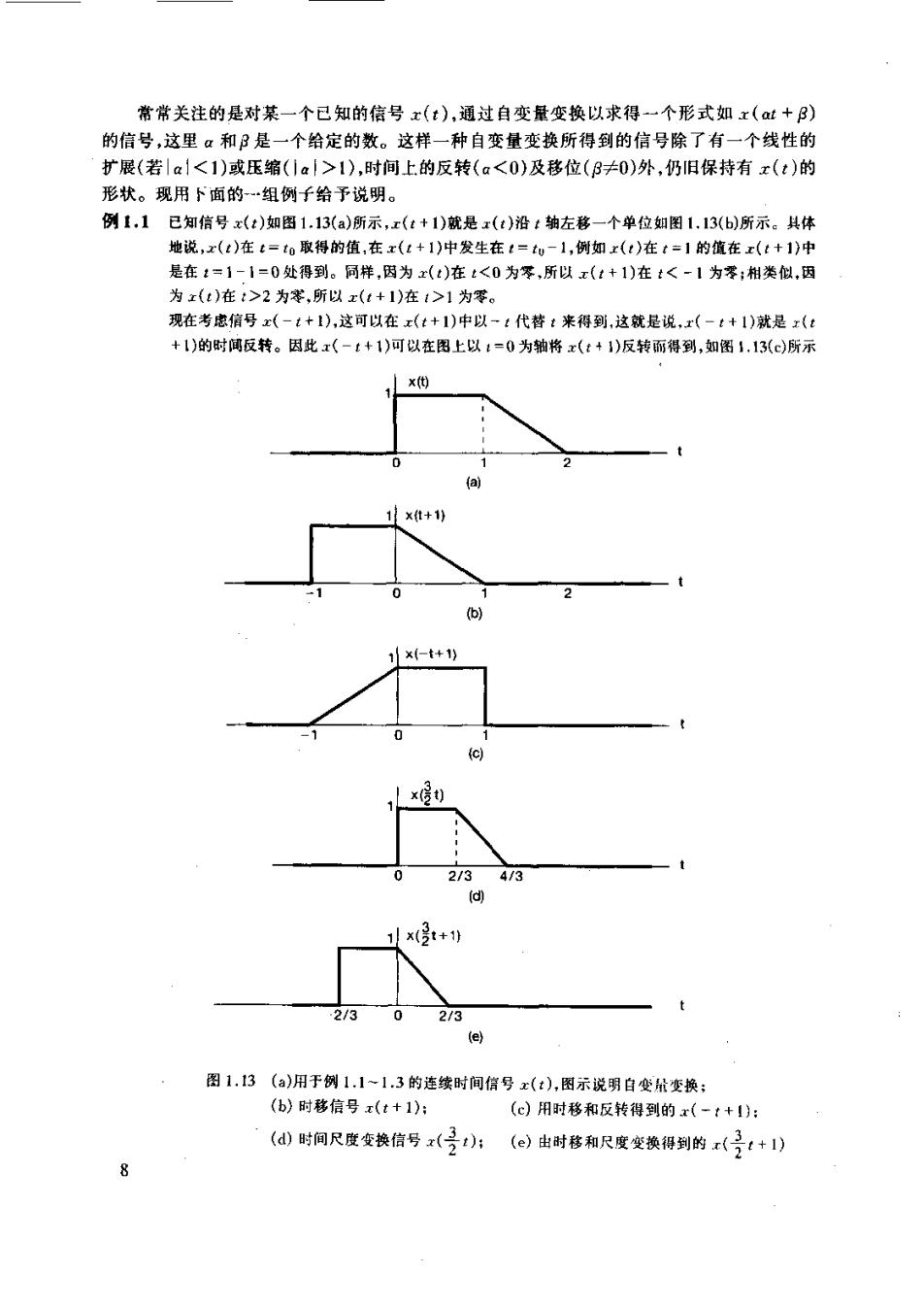
常常关注的是对某一个已知的信号x(t),通过自变量变换以求得一个形式如x(吐+B) 的信号,这里α和是一个给定的数。这样一种自变量变换所得到的信号除了有一个线性的 扩展(若|a1<1)或压缩(a>1),时间上的反转(a<0)及移位(B≠0)外,仍旧保持有x(t)的 形状。现用下面的一组例给予说明。 例1.1已知信号x(z)如图1.13(a)所示,x(t+1)就是x(t)沿:轴左移一个单位如图1.13(6)所示。其体 地说,x(t)在t=t0取得的值,在x(t+1)中发生在=-1,例如x(:)在t=1的值在x(t+1)中 是在:=1-1=0处得到。同样,因为x()在<0为,所以x(t+1)在t人-1为零;相类似,因 为x()在:>2为零,所以x+1)在1>1为零 现在考虑信号x(-t+1),这可以在x(t+1)中以-1代替:来得到,这就是说,x(-t+1)就是(t +1)的时闻反转。因此x(-1+1)可以在图上以:=0为轴将x(:+1)反转而得到,如图1.13(c)所示 x代 +1 2/3 t+ 图1.3(a)用于例1.1-1,3的连续时间号x(t),图示说明自变变换: (b)时移信号x(t+1): (c)用时移和反转得到的x(-t+I: (d)时间尺度变换信号x(号):(e)由时移和尺度变换得到的x(子:+1)

例1,2已知信号x(:)如图1.13()所示,信号x(号)就相应于x()以因子23作线性时间压缩,如图 1.13()所示。具体一点就是x(:)在1=t0所取得的值,在x(号t)中是在t=子o时刻得到。例 如,x(:)在1=1时的值,在x(号)中是在t=子(1)=子求得。同样,因为x(:)在t<0为零,所 以有x(号)在t<0也为零;因为x()在>2为零,所以x(号)就在t>43时为零。 例1,3假设对于一个给定信号x(t),趣看看自变量变换的效果,以求得一个形如x(+3)的信号,这里 ?,P都是已知的某个数。为此,一种有条不素的途径是首先根据日的值将x《)延时或超前,然后 再银据。的值来对这个已经惩时或超前的信号进行时同尺度变换和/成时阀反转。如果|<1 就将该已延时或超前的信号进行线性扩展:如果。>1,就实行战压罐,若。<0就再作时 间反转。 为了说明这个办法,看看x(号:+1)是怎么由图1.13(a)的x()求得的。因为日=1,所以首先将 x()超前1(即左移1),如图1.13(b)所示。因为a=32.所以就应将图1.13(b)已左移的信号线 性压笔,压馏因子是23,于是就得到如图1.13(e)所示的信号,这就是x(号:+1)。 自变量变换除了在表示一些物理现象(如声纳信号的时移、磁带的快放或倒放等)中的应 用外,它在信号与系统分析中是极为有用的。在1.6节和第2章都将应用自变量变换来引入 和分析系统的性质。这些变换在定义和研究信号的某些重要性质上也是很重要的。 1.2.2周期信号 在全书中都会常常遇到的一类重要信号就是周期信号。一个周期连续时间信号x(:)具 有这样的性质,即存在一个正值的T,对全部:来说,有 x(t)=x(t+T) (1.11) 换句话说,当一个周期信号时移T后其值不变。这时就说x(:)是一个周期信号,周期为T。 周期的连续时间信号出现在各种场合。例如在习题2.61中所说明的具有能量储存系统的自 然响应,像无电阻损耗的理想LC电路和无摩擦损耗的理想机械系统的自然响应都是周期的; 而且事实上它们都是由一些基本的周期信号所组成的,这些都将在1.3节讨论。 图114连续时间周期信号 图1.14给出了一个周期连续时间信号的例子。从该图或者从(1,11)式都能很快得出:如 果x(:)是周期的,周期为T,那么对全部:和任意整数m来说就有x(t)=x(:+mT),由此 x()对于周期2T,3T,4T,.等等都是周期的。对于使(1.11)式成立的最小正值T称为 x(t)的基波周期Ta。除了r(:)为一个常数外,基本周期的定义都成立;在x()为一常数的