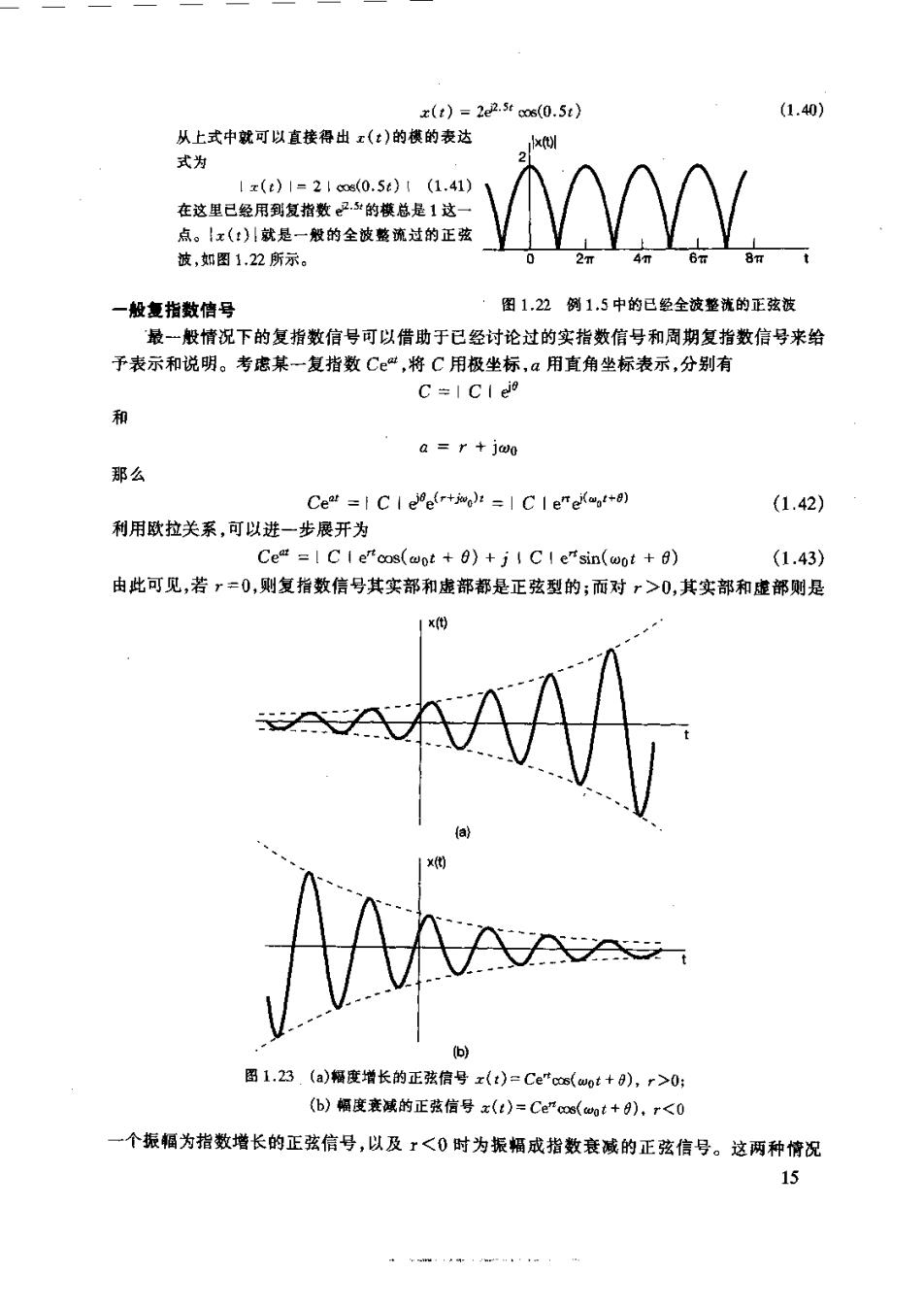
x(t)=22.5tco6(0.5t) (1.40) 从上式中就可以直接得出x(:)的模的表达 式为 1x(t)1=21(0.56)1(1.41) 在这里已经用到复指数2的模总是1这 点。!x(:)川就是一般的全波整流过的正弦 放,如图1.22所示。 一般复指数信号 图1,22例15中的已经全液整的正弦被 最一般情祝下的复指数信号可以借助于已经讨论过的实指数信号和周期复指数信号来给 予表示和说明。考虑某一复指数Ce“,将C用极坐标,a用直角坐标表示,分别有 C=IC I e 和 a r jwo 那么 Cear =Cle(rtis):=Cl eeoo+0) (1.42) 利用欧拉关系,可以进一步展开为 Ceat =I C I e"oos(wpt +0)+j Cle"sin(wot+) (1.43 由此可见,若r=0,则复指数信号其实部和虚部都是正弦型的;而对r>0,其实部和虚部则是 (b) 图1.23.(a)幅度增长的正弦信号x(:)=Ce*cs(aot+0),r>0: (b)幅度衰诚的正弦信号x(:)=Ceos(cot+),r<0 一个振辐为指数增长的正弦信号,以及r<0时为振桶成指数衰减的正弦信号。这两种情况 15

如图1.23所示,图中的虚线对应于函数±1C引e。由(1.42)式知道|C引e是复指数信号的据 犒,可见C®起着一种振荡变化的包络作用,也就是说每次振荡的峰值正好落在这两条虚线 上。这样,包络线给我们提供了一个十分方便的工具,使得我们可以看出振荡辅度的变化趋 数 具有指数衰诚振幅的正弦信号常称为阻尼正弦振满,RLC电路和包括有阻尼和恢复力在 内的机城系统(例如汽车或展系统)的响应都是这样一个指数衰诚振荡的例子。这样一类系统 都具有这样的过程:随着在振荡衰减的过程中,由电阻、摩擦等阻力消耗掉能量。在习题2.61 和2.62中还能见到这样的系统,以及它们有阻尼的正弦自然响应的例子。 1.3.2离散时间复指数信号与正弦信号 与连续时间情况下一样,一种重要的离散时间信号是复指数信号或序列,定义为 xn]=Ca (1.44) 这里C和α一般均为复数。若令a=,则有另一种表示形式为 x「t1=Cc0# (1.45) 虽然从形式上看,(1.45)式更加类似于连续时间复指数信号的表达式(1.20)式,但是在离散时 间情况下,往往把离散时间复指数序列写成(1.44)式更为方便和实用些。 实指数信号 如果C和a都是实数,那么就会有如图1.24所示的几种特性。若!a>1,信号随n指数 增长;la<1,则随n指数衰减。另外,若a是正的话,则C的全部值都具有同一符号;而当 a为负时,则x(n]的值符号交替变化。同时也注意到若a=1,x[n]就是一个常数;而当 a一-1时,x[m]的值就在+C和一C之间交替改变。实离散时间指数序列可以用来描述诸 如人口增长作为“代”的西数、投资总回收作日、月、或季度的函数等这样一些问题。 正弦信号 如果将(1.45)式中的局限为纯虚数(即1a=1)的话,就可以得到另一个重要的复指数 序列。具体地考虑如下序列: x[n]=eo" (1.46) 和连续时间情况一样,这个信号是与正弦信号密切相关的,即 x[n】=Acos(aon+) (1.47) 若取:无量纲的话,那么0和的章纲都应是弧度。图1,25中示出了三个正弦序列的例 子。 和前面作法一样,利用欧拉公式可以将复指数和正弦序列联系起来为 (1.48) Acos(won+p)=号ee,n+号eie (1.49) (1.46)式和(1.47)式的信号就是在离散时间信号中具有无限总能量,而有有限平均功率的例 子。因为1,1=1,(1.46)式中信号的每个样本在信号能量中的贡献都是1。因此,在-∞ 16
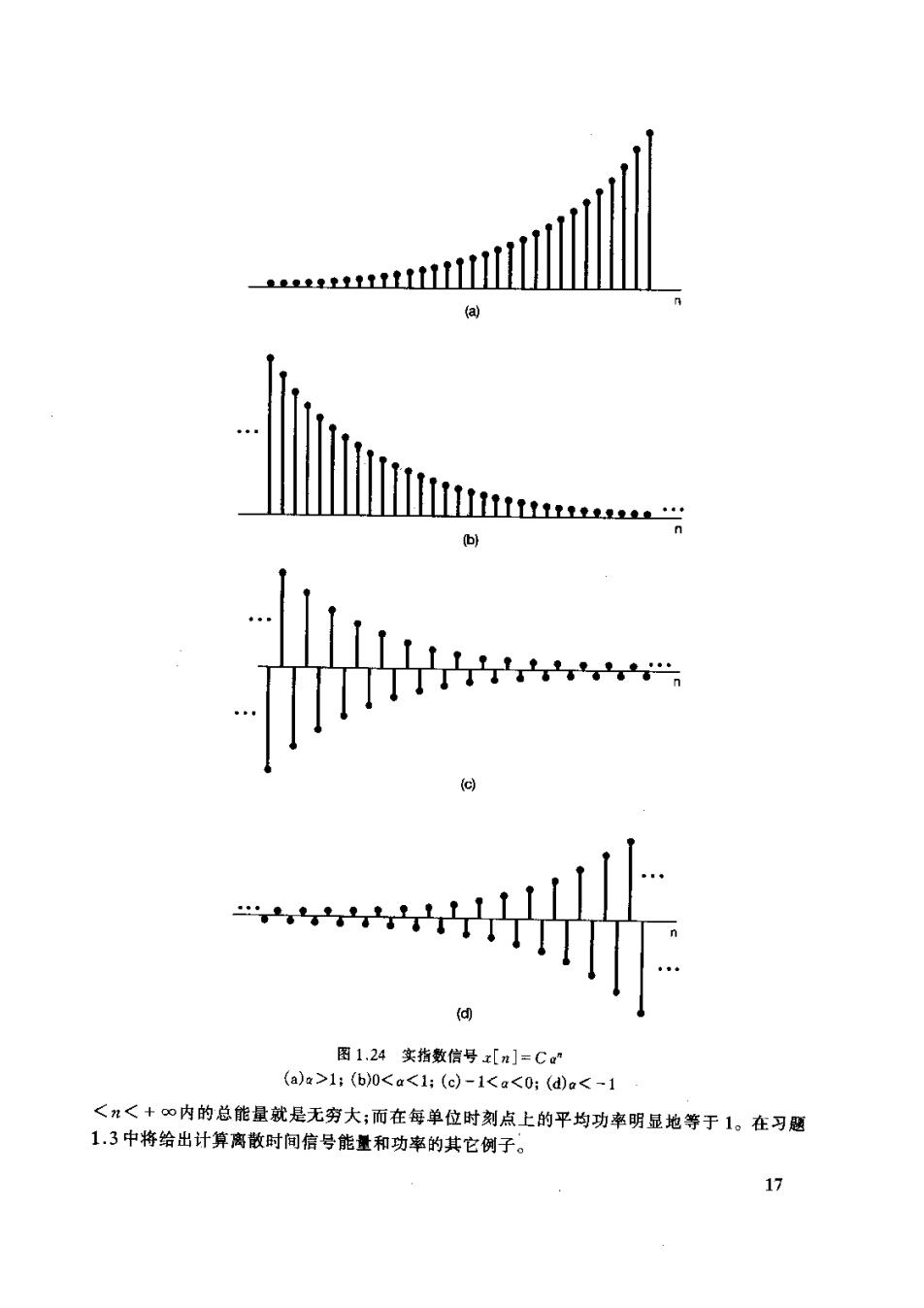
-片 图1,24实指数信号x[n]=C (aa>1:(b)0<a<1:(d)-1<a<0:(d)a<-1 <n<+∞内的总能量就是无穷大;而在每单位时刻点上的平均功率明显地等于1。在习题 1.3中将给出计算离散时间信号能量和功率的其它例子。 17

x阿=cosn6) 图1.25离散时间正弦信号 一般复指数信号 一般离散时间复指数信号可以用实指数和正弦信号来表示。将C和。均以极坐标形式 给出,即 C=

a=lal emo 则有 Ca"=1 Cll a l"oos(won +)+j!Clla l"sin(won +8) (1.50 于是,对|a=1,复指数序列的实都和虚部都是正弦序列。对|a|<1,其实部和虚部为正弦序 列乘以一个按指数衰减的序列。对1.1>1,则乘以一个按指数增长的序列。图1.26示出了 这些信号的例子。 . iii 图1.26(®)增长的离散时间正弦信号:(b)减的离散时间正弦信号 1.3.3离散时间复指数序列的周期性质 虽然在连续时间和离散时间信号之间有很多相似之处,但是也存在一些重要的差别。其 中之一就是来看看离散时间指数信号e,”。在1.3.1节,与其对应的连线时间信号。,具有 以下两个性质:(1)w0愈大,信号振荡的速率就愈高:(2)e对任何值都是周期的。现在, 将在这两点上来考装一下,就会看到在这两个性质上,两者是肯定不一样的。 第一个性质的不同直接来自于离散时间和连续时间复指数信号之间另一个极为重要的不 同之处。为此,研究一下顿率为0+2π的离散时间复指数信号: (1.51) 从(1.51)式说明,离散时间复指数信号在领率0+2π与频率0时是完全一样的。这一点和 连续时间复指数信号。是完全不同的,在那里,不同的就对应着不同的信号;而在离散时 19