
11.2.3不稳定系统的稳定 (596) 11.2.4米样数裙反系统 (599) 11,2.5装踪系统. (600 11.2.6反绩引起的不稳定 (602】 11.3线性反情系统的根轨速分析法 (604 11.3.1 604 11.3.2闭环极点方程 1605 11.3,3根轨迹的端点:K=0和K|■+四时的闲环板,点 (606 11.3.4角判据. (607 11.3.5根轨迹的性质 (610 1.4奈查斯特稿定性判据 (615) 11.4,1图线性质 (616) 11.4.2连续时间LTI反情系就的奈查斯特判搭, (618 1.4.3离散时间LT1反馈系统的奈奎斯特判抵 11.5增益和相住裕度 6 624) 11.6 小结 (631) 习那44. (631】 附录部分分式展开 1661 (671) 第一部分基本题答案. .(680j

第1章信号与系统 1.0引言 在崩面绪论中已经提到,信号与系统概念出现在极为广泛的各种领城中。然而,在本书中 将会看到,其中存在着一种分析体系,也就是说一种描述信号与系统的语言和一整套分析它们 的强有力的方法,而这种语言和方法都能很好地应用于这些领域中所要解决的问题。本章就 是从引人信号与系统的数学描述及其表示人手来建立这样一种分析体系的。紧随其后的几 章,凭借这个基础来建立和描述另一些概念和方法,而这些又会大大加强对信号与系统问题的 理解,以及在分析和解决涉及多个方面的信号与系统问题的能力。 1.1连续时间和离散时间信号 1.1.1举例与数学表示 信号可以描述范圈极为广泛的一类物理现象。 虽然信号可以用许多方式来表示,但是在所有的情 况下,信号所包含的信息总是寄高在某种变化形式 的波形之中。考虑一下图1.1这个简单电路,此时 电压源,和电容器上的电压u,的变化形式都是可 以作为信号的例子。类似地,示于图1.2的外作用 力f及所得到的汽车速度。随时间的变化也都是 信号的例子。作为另一个例子,考虑一下人的声道 图1.1含有电压源和电容器 系统,该系统根据在声压上的起伏变化而产生语音 电压,的简单电路 信号。图1.3示出某一段语音信号的录音被形,它 是通过拾音器来感受到声压的变化,然后再转换为某种电 信号。由图可见,不同的语音相应有不同的声压变化被形 并声道系统产生的可懂语言就对应着一串特定的被形 另外,示于图1.4是一幅黑白照片,这时整个照片上各点的 亮度变化波形才是面重要的。 图12一部汽车。∫系来自发动 在数学上,信号可以表示为一个或者多个变量的函数。 机的外加力,风系正比于 例如,一个语音信号就可以表示为声压随时间变化的函数: 汽车速渡的章擦力 一张黑白照片就可以用亮度随二维空间变量变化的函数来表示。本书的讨论范围仅限于单 变量的函数,而且为了方便起见,以后在讨论中一般总是用时间来表示自变量,尽管在某些具 体应用中自变量不一定是时间。例如,在地球物理学研究中,用于研究地球结构的一些物理量 像密度、气腺度和电阻率等就是随地球深度变化的信号:在气象观察中,有关气压,温度和风速 1
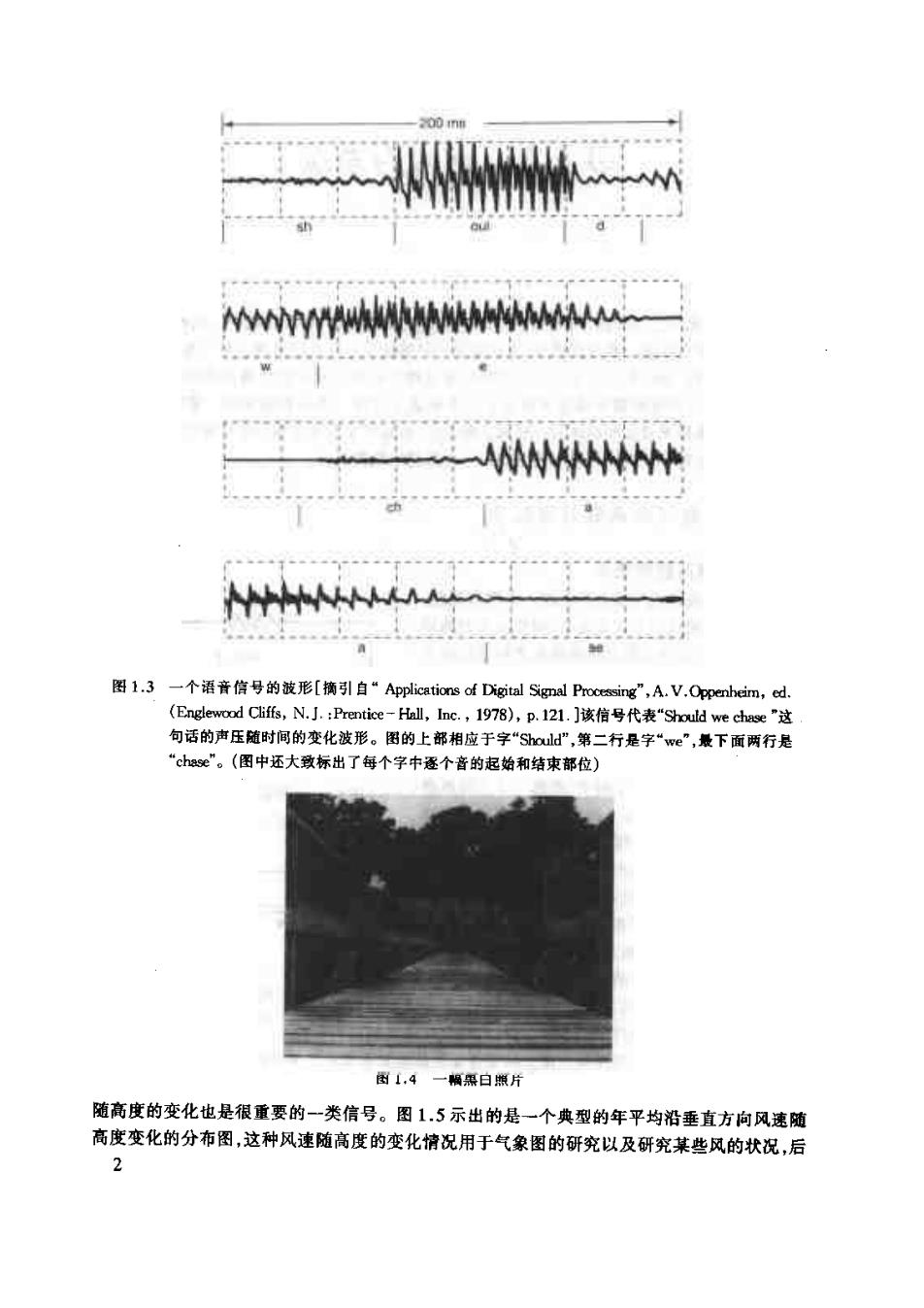
WWWWW 图1.3一个语音信号的波形[摘引自“Applications of Digital Signal Procing”,AV.Oppenbeim,cd. (Englewood Cliffs,N.J.:Prentice-Hnl,lnc.,1978),P.121.]该信号代表“Should 句话的声压随时间的变化波形。国的上部相应于字 hould”,第 二行是字“w心”,最下面两行是 "chae”。(图中还大致标出 每个字中逐个音的起始和结束位) 图1.4一幕白照片 随高度的变化也是很重要的一类信号。图1.5示出的是一个典型的年平均沿垂直方向风速随 高度变化的分布图,这种风速随高度的变化情况用于气象图的研究以及研究某些风的状况,后
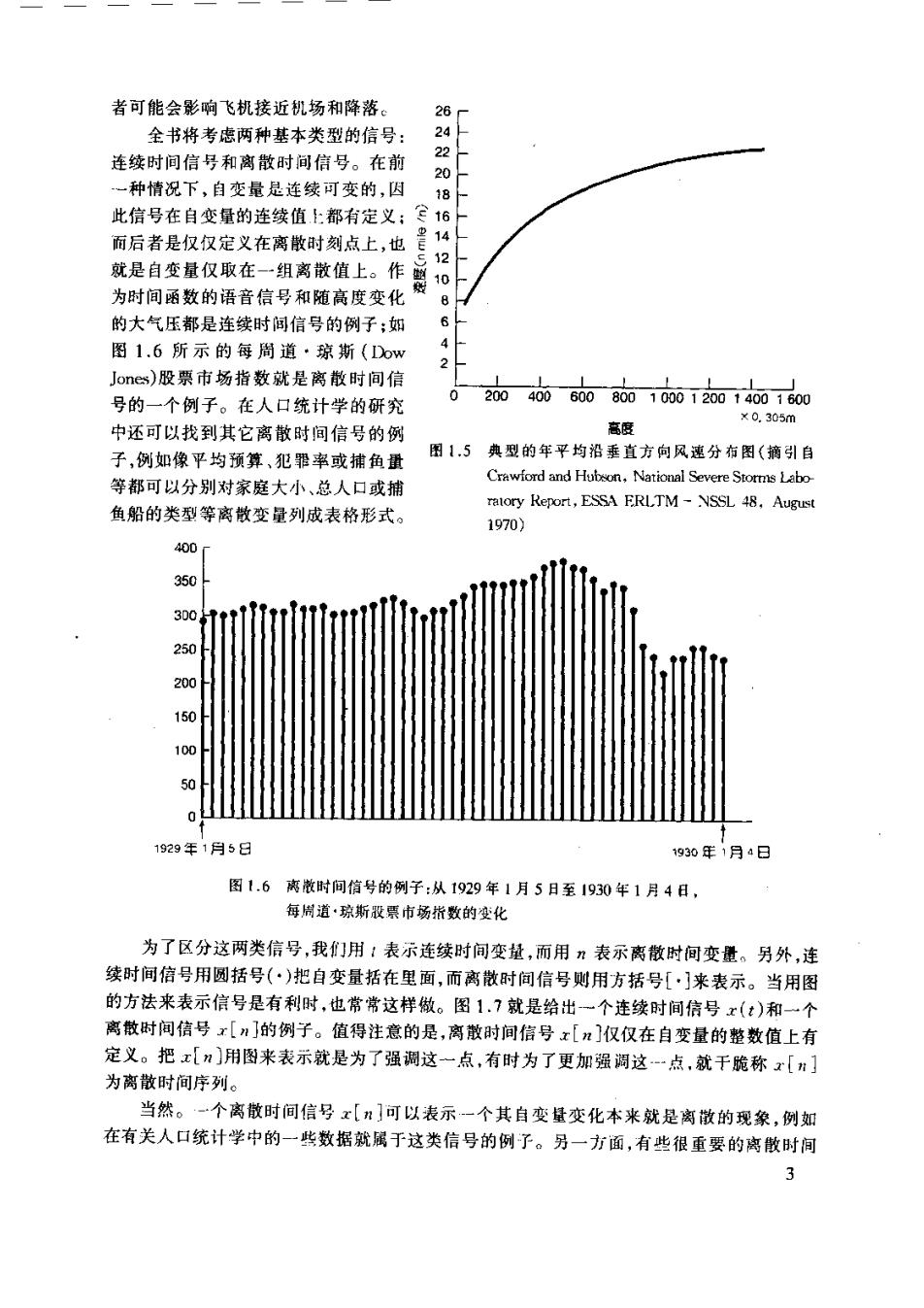
者可能会影响飞机接近机场和降落。 26 全书将考虑两种基本类型的信号: 连续时间信号和离散时间信号。在前 一种情况下,自变量是连续可变的,因 此信号在自变量的连续值上都有定义: 而后者是仅仅定义在离散时刻点上,也 就是自变量仅取在-一组离散值上。作 为时间函数的语音信号和随高度变化 的大气压都是连续时闯信号的例子:如 图1.6所示的每周道·琼斯(Dow Jones)股票市场指数就是离散时间信 号的一个例子。在人口统计学的研究 204096d0a001001201400160 X0.305m 中还可以找到其它离散时间信号的例 高 子,例如像平均预算,犯罪率或捕角重 困1.5典型的年平均沿垂直方向风速分布图(摘引自 等都可以分别对家庭大小、总人口或捕 Crawiord and Hubon.National Severe Storms Labo 鱼船的类型等离散变量列成表格形式。 ratory Report,ESSA ERLTM-NSSL 48.August 1970) 400 350 300 2 200 150 100 0 929年1月5日 930年1月4日 图1.6离散时间信号的例子:从1929年1月5日至1930年1月4日, 每周道·琼斯股票市场指数的化 为了区分这两类信号,我们用!表示连续时间变量,而用”表示离散时何变量。另外,连 续时间信号用圆括号(·)把自变量括在里面,而离散时间信号则用方括号[·】来表示。当用图 的方法来表示信号是有利时,也常常这样做。图1.7就是给出一个连续时间信号x(t)和一个 离散时间信号x[J的例子。值得注意的是,离散时间信号x[n]仅仅在自变量的整数值上有 定义。把x[n]用图来表示就是为了强调这一点,有时为了更加强调这一点,就干脆称[] 为离散时间序列。 当然。一个离做时间信号x[n]可以表示一个其自变量变化本来就是离放的现象,例如 在有关人口统计学中 一些数据就属于这类信号的例子。另一方面,有些很重要的离散时间 3

b 图1.7信号的图形表示:(a)连续时间信号:6)离散时间信号 信号则是通过对连续时间信号的采样而得到的,这时该离散时间信号x[n】则代表了一个自 变量是连续变化的连续时间信号在相继的离散时刻点上的样本值。由于近代数字处理器在速 度、计算能力及灵活性等方面的进展,因此被用来实现许多这样的实际系统,其范围涉及从数 字自动驾驶仪到一般的数字音频系统。.这样的系统都要求利用代表连续时间信号经采样过的 离散时间样本序列,这就是飞机的位置、速度和航向,或是音颍系统的语音和音乐。同样,报纸 以及本书中所用的照片实际上也都是由很多细小的点格所组成的,其中每一点就代表着相应 于原照片上该点亮度的采样。无论这些离散时间信号来源是什么,信号x[π]总是在n的整 数值上有定义,因此像所谓一个数字语音信号的第32个样本,以及对某一家庭的27个家庭 成员的平均预算等等都是毫无意义的。 本书大部分都采用分别地,但是并行地讨论离散时间信号和连续时间信号,以使我们能在一种 信号类型中所获得的细节有助于对另一种信号类型的理解。到第7章再回到采样问题中来,这样 我们就可以把连续时间信号和离散时间信号的概念结合起来,以披露这两种信号之间的关系。 1.1.2信号能量与功率 从到目前为止所给出的例子可以看到,信号可以表示范围很广的一些现象。在很多(但不 是全部)应用中,所考虑的信号是直接与在某一物理系统中具有功率和能量的一些物理量有关 的。例如,若()和(2)分别是阻值为R的某-.电阻上的电压和电流,那么其瞬时功率就是 p()=()i(t)=京2(t〉 (1.1) 在时间间隔t4≤t≤红内消耗的总能量就是 p)d-最:)r (1.2) A