
§1.3平面点集的一般概念 ·15· 故用公式(1.15)计算得 之=[2(cos0+isin0)门]3=2(cos 2ki sin 3 k=0,1,2. 所以方程之=2有3个解,它们是 ,(-日+.(- 2 2 [注在复数中2开3次方根有3个值,它们的模都是2的3次方 根中取正实数的那一个,即算术根.] §1.3乎面点集的一般概念 §1.3.1开集与闭集 在第一节中已经说过,对于一个复数与它所对应的平面上.的点我 们将不加区分,因此点可以用复数表示,而复数可看作点.对于一些特 殊的平面点集,我们将采用复数所满足的等式或不等式来表示 平面上以z为中心,(任意的正数)为半径的开圆表示为: |z-2。|<6, 称它为z的邻域,面称由不等式0<|z一z。{<8所确定的点集为。的 去心邻域. 设G为一平面点集: (1)。为G中任意一点.如果存在之的一个邻域,该邻域内的所 有点都属于G,那么称。为G的内点.如果G内的个点都是它的内 点,那么称G为开集, (2)平面上不属于G的点的全体称为G的余集,记作G①,开集 的余集称为闭集。 (3)是一点,若在。的任一邻域内既有(G的点又有(G的点,则 ①G的余集,在集合论中,有时记为CG
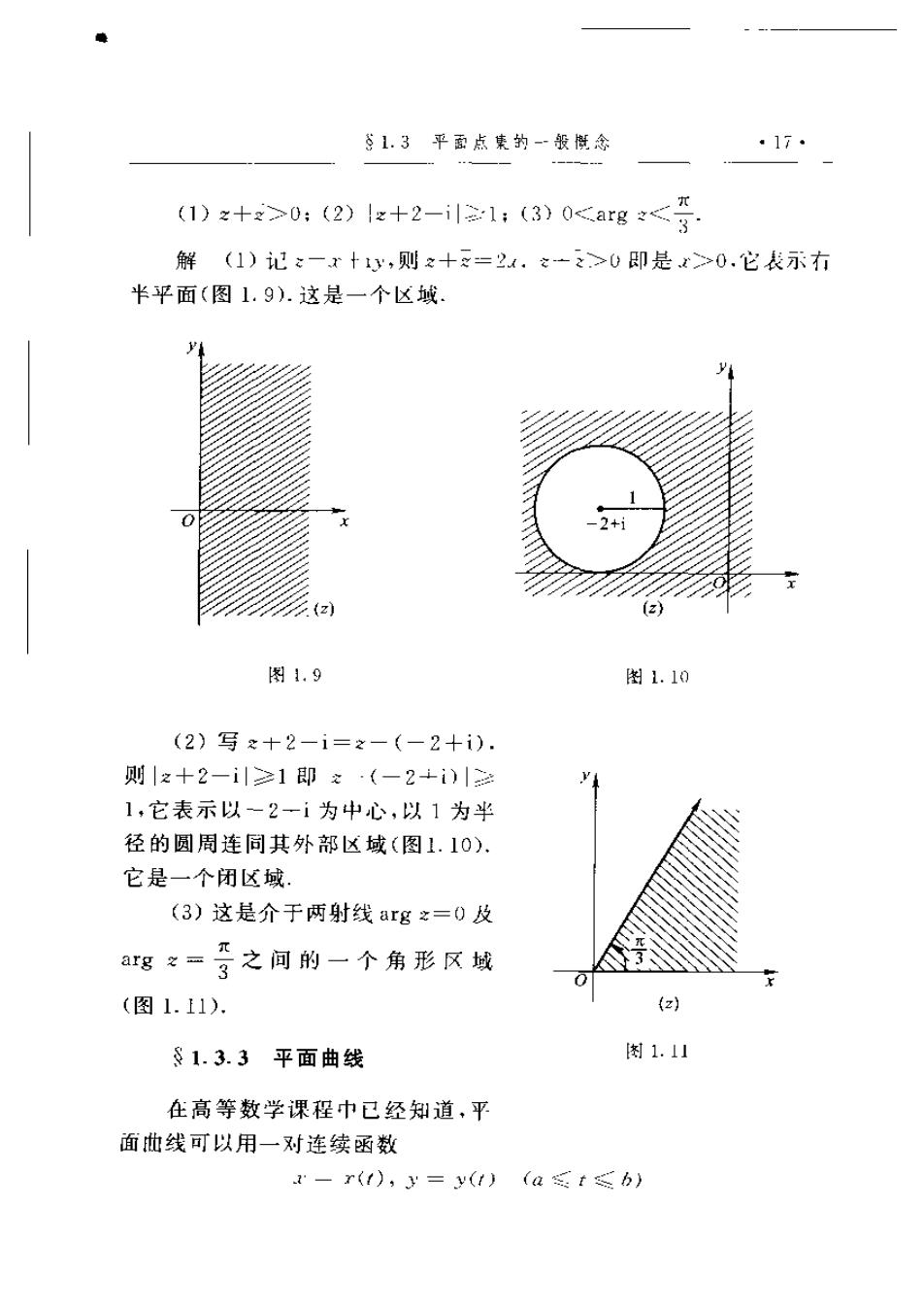
§1.3平面点集的-般概念 ·17. (1)z+>0:(2)z+2-i≥1:(3)0<arg2<g 解(1)记x一x十y,则之十=2.之一>0即是x≥0.它表示右 半平面(图1.9).这是一个区蜮。 2+i z 图1.9 图1.10 (2)写之+2-i=x-(-2+i). 则|之十2一i川≥1即之·(一2+i)| 1,它表示以一2一i为中心,以1为半 径的圆周连同其外部区域(图1.10). 它是一个闭区域 (3)这是介于两射线arg之=0及 ag:=子之间刷的一个角形风域 (图1.11). (z) 81.3.3平面曲线 刻1.11 在高等数学课程巾已经知道,平 面地线可以用一对连续函数 一r(1),y=y(1)(atb)

典 ·18· 第一章复数与复变函数 来表示(称为曲线的参数方程表示).我们现在用实变数的复值函数 之(t)来表示,即 (t)=x(t)+iy(t)(atb) 例如,以坐标原点为中心,以《为半径的圆周,其参数方程可表示为 r =ucos t,y=asin t (0 2). 写成复数的形式即为 e-u(cost十isin1)(0ts2π). 又如,平面上连接点(x1y)与(x:)的直线段,其参数方程可表示为 x二x1十(2一T)t,y=y1+(:-,)t(0f1). 从复平面上看,这就是连接点,=x1十iy,与点=x十i:的直线段. 故其复数形式的参数方程可表示为 z=1十(g2一21)t(0签11) 除了参数表示以外,通常我们还用动点?所满足的关系式来表示 曲线.例如把以之一0为中心,以4为半径的圆周,表示成为x|=::平 行于虚轴且通过点之=1的直线,从1一i到1+i的一段可表示成 Rez=1(1≤Im≤1)等等. 如果在区间at≤b上x(t)和y(t》都是连续的.且对于1的每一 个值、有 [x(t)]+[y'(t)]≠0. 那么这曲线称为光滑的,由几段依次相接的光滑曲线所组成的曲线称 为分段光滑曲线 设C:之=之(t)(a≤t≤b)为一条连续曲线,2(a)与z(b)分别称为( 的起点与终点,对于满足<t:b、a≤t2≤五的t1与t2,当t,≠1:而有 z(t1)一z(t2)时,点z(t1)称为曲线(的重点.没有重点的连续曲线(, 称为简单曲线或若尔当(Jordan)曲线.如果简单曲线C的起点与终点 重合,即之(a)=z(),那么曲线C称为简单闭曲线(图1.12()).由此 可知,简单曲线自身不会相交.图1.12(c)与1.12(d)都不是简单曲线. 若尔当曲线定理任一简单闭曲线将平面分成两个区域.它们都 以该曲线为边界.其中…个为有界区域,称为该简单州曲线的内部:另 一个为无界区域,称为外部:
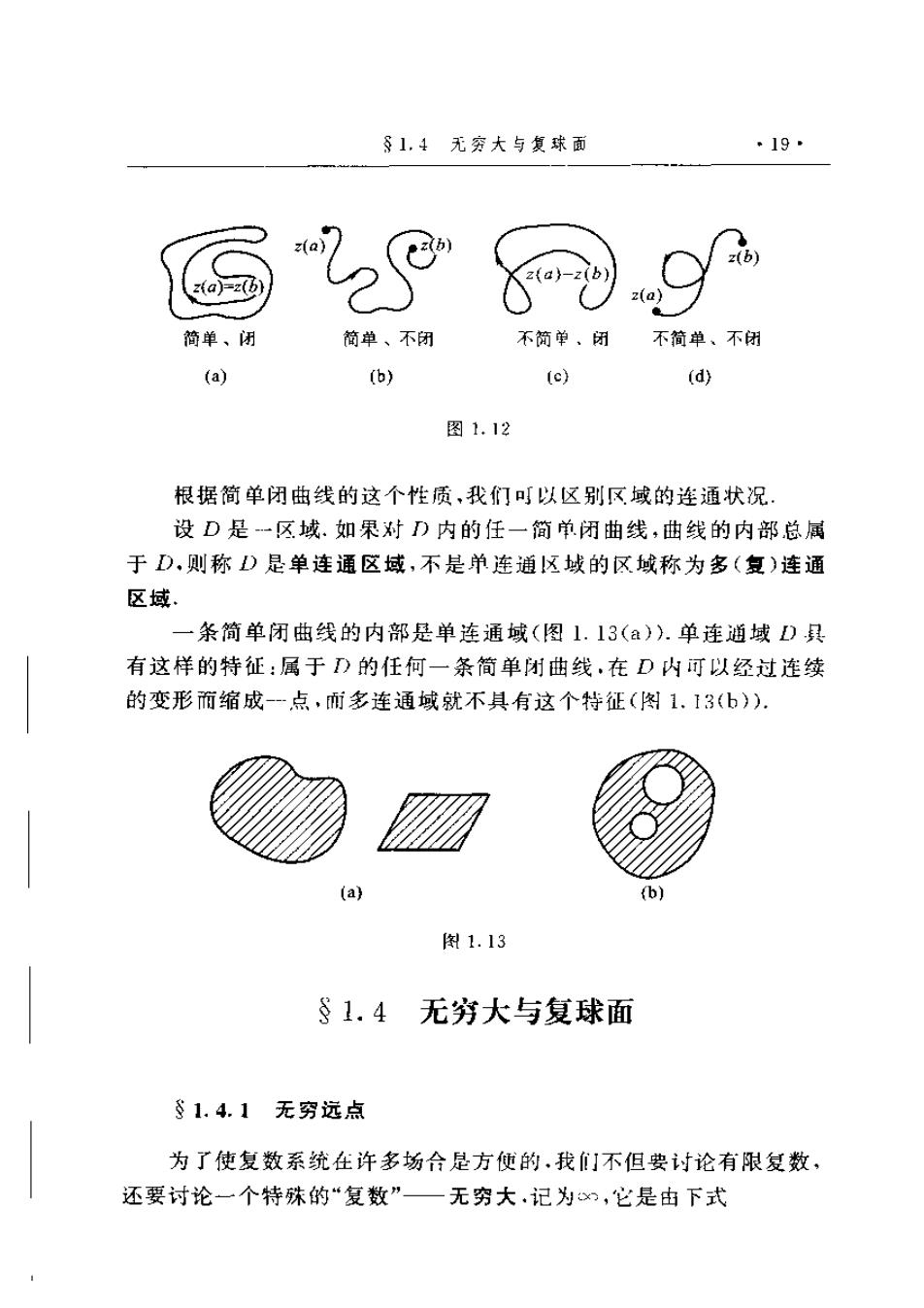
§1,4无穷大与复球面 ·19 xa)2(b) z{d》-z z(a) 简单、闭 简单、不闭 不简单,闭 不简单、不闭 (a) (b) (c) (d) 图1.12 根据简单闭曲线的这个性质,我们可以区别区域的连通状况! 设D是一区域.如果对D内的任一简单闭曲线,曲线的内部总属 于D,则称)是单连通区域,不是单连通区域的区域称为多(复)连通 区域 一条简单闭曲线的内部是单连通域(图1.13(a)).单连通域)县 有这样的特征:属于D的任何一条简单闭曲线,在D内可以经过连续 的变形而缩成点,而多连通域就不具有这个特征(图1.13(b)). (a} (b) 图1.13 §1.4无穷大与复球面 §1.4.1无穷远点 为了使复数系统在许多场合是方便的,我】不但要讨论有限复数, 还要讨论一个特殊的“复数”一无穷大·记为x,它是由下式

·20· 第一章复数与复变函数 1 0 来定义的.它和有限数的四则运算定义如下: (加法)a十cx=x0十a=x (azoo) (减法)9一u=x、a一x=x (a≠∞) (乘法) a·=cx·a= (a≠0)》 (除法) 8=0,9=∞ (a≠3) 在这种定义下,一向不能以0为除数的除法,现在可能了.但要注意, X士Cx, 0·,0·0, 8 都无意义· 对于复数∞而言,其模规定为+x,而实部、虚部和辐角均没有意 义.对于其它的每-个复数z,都有之!<十×,相比较而言称之为有限 复数 在复平面上没有一点与∞相对应,但我」可设想复平面上有一理 想点与它对应,此点称为无穷远点.复平面加上无穷远点称为扩充复 平面,扩充复平面上的每一条直线都通过无穷远点, [注包括无穷远点自身在内且满足z>M的所有点的集合·其 中实数M>0,称为无穷远点的邻域.换言之,无穷远点的邻域是包括 无穷远点自身在内的圆周引z=M的外部.不包括无穷远点自身在内, 仅满足|z>M的所有点的集合,称为无穷远的去心邻域,它可表示为 M<z<+o.] §1.4.2复球面 我们知道,把复数表示成复平面上的点或向量,都是由于实际需要 而采取的表示方法(正如同数学是从实践中产生).由于实际需要还可 以用其他方法表示复数,例如,在地图制图学中考虑到球面与平面上点 的对应关系,即把地球投影到平面上去进行研究.这种方法叫做测地投 影法.我们利用这种方法,以建立全体复数与球面上的点之间的一一对 应关系,于是用球面上的点来表示复数,进而确立了∞的几何意义