
·2 第一章复数与复变函数 以看作纯虚数0i. 设1=x,十iy1与2=x2十iy2是两个复数.如果x1=x2y=y,则 称,与2相等.由此得出,对于复数之=x+y,之=0当且仅当 x=y=0. 设之=x十iy是一个复数,称x一iy为之的共轭复数,记作.易知 ()=之.共轭复数有很多用处,后文将逐步介绍 §1.1.2复数的四则运算 设之1=x1十iy1z2=x2十iy2是两个复数.定义复数的加法为: 之:+22=(x1+x2)+i(y1+y2). (1.1) 复数的减法是加法的逆运算.如果存在复数心使之1=之,十之,则 之=z1一22·因此得到 21-z2=(x1-x2)+i(y1一y2). (1.2) 定义复数的乘法为: z1·22二(r1x2y1y2)+i(x:y+2ey1). (1.3) 例如 (2-31)(4+5i)=[2·4-(-3)·5] +[2·5+(-3)·] =23-2i. 由乘法定义可验证 i·i=(0+1·i)(0+1·i)=-1. 复数的滁法是乘法的逆运算.当2≠0时,我们说:“,除以之,得 到商x”,意思就是 21=22·2 从这个式子我们来求之.记之=x十iy.由于 x,+iy=(x2+iy2)(x+iy) =(x2x-y2y)+i(x2y+xy2). 根据两个复数相等的定义,得到 I=x -y2y,y,=Ty+ry2

4 第一章复数与复变函数 e分红十动,m8一a- 例1.1设之,之2是任意两个复数,求证: 2Re(zz2)=2:22十z1z2 证 利用公式Re之=号(2十x)可算得 2Re(x122)=之1z2十(222) =1之2十之182之22十212 学习了以:两段以后,读者可仔细体会,以加深对复数的认识.最 初当给出复数概念时,我们所知道的复数是什么?复数无非是一个实数 x同另一个实数y用“”及“+”连接而写成“x+y”这样一个形式的东 西,“”是什么,“十”是什么意思,都未加说明.后来,介绍了复数与实数 的关系,复数与纯虚数的关系,又介绍了复数加法的定义.这样,我们也 就可以把x十iy看成实数x同纯虚数iy相加.其后,又定义了复数乘 法.利用复数的加法与乘法,现在已可将复数之=x十y真正理解为虚 数i乘y,然后再加上x的结果(注意x=x十i0,y=y+i0,i=0十1i): 之=(x+0)+(0+1·i)(y+0i)=x+iy. 历史上,当人们第一次引进一1的平方根并把它当作“数”的时候,是把 它作为想像中的数,所以称为“虚数”,后来就把形如x十y的数叫做复 数,意思是“复合”起来的数. §1.1.3复平面 一个复数x十iy可唯一地对应一个 有序实数对(x,y).而有序实数对与坐标 y 平面上的点是一一对应的.所以,复数 ◆+iy 全体与坐标平面上的点的全体形成一一 对应.现在我们直截了当地把坐标平面上 的点写成x十iy(图1.1),那么,横轴上 的点就表示实数.纵轴上的点就表示纯虚 数.整个坐标平面可称为复(数)平面.今 图1.1

$1.2复数的三角表示 45 后我们索性将复数与复平面的点不加区分,这种点,数等同将给我们带 米许多方便.在点、数等同的观点下,一个复数集合就是一个平面点集. 因此,很自然地.某些持殊的平面点集就叮以用复数所满足的某种关系 式来老示.例如、 i2:1mg20} 与 {z:0≤Re之1,0sImg1} 分别表示上:半平面与以0,1,1±i,i为顶点的正方形 §1.2 复数的三角表示 S.2.1复数的模与辐角 上面说过,复数与平面上的点作成一-·对应,这是将复数实部与虚 部分别看作直角丝标系下点的横坐标与纵坐标.除此以外,复数还可以 同平面向量作成对应、只要将复数的实部与 虚部分别看作向量的水平分量与铅垂分量就 行了.所以我们也可以把复数与平面向量等 x+iy 同起来.不过要注意,向量具有平移不变性, x+iy 即其起点可安放在任意一点.如果把向量的 起点放在(复平面的)坐标原点,则此向量及 0 向量的终点在上述两种对应下恰好对应同- 个复数(图1.2). 图1.2 如果之是一个不为0的复数,我们把它所对应向量的长度叫做之 的模,记作|2|:把它所对应向量的方向角叫做之的辐角.辐角有无穷多 个值,其中任意两个值相差2π的整数倍.今后,我们用记号Ag之作为 之的辐角的一般表小,意思是它可以不受限制地取之的辐角的任意值、 再用记号arg之表示x的所有辐角中介于一元与π之间(包括π)的那一 个角,并把它称为之的主辐角,即一π<rg之≤π(顺便指出、有的书:

·6* 第一章复数与复变函数 把z的所有辐角中的非负最小值作为主辐角,也用记号rg之表示.这 样便有0≤arg之<2π).所以 Arg之=arg之十2kπ, Arg Z Arg z arg z (2) 图1.3 及是任意的整数(图1.3).当之=0时,「2|=0,这时辐角没有意义.对于 共轭复数,我们有之|=必|以及arg之=-arg之(z≠0且不为负实数, 对负实数有arg之=arg之=x).对z÷x十iy易验证 lz=√2+y, 因此 z2=x2+y2=之之, 由此推出 对于一个不为0的复数g=x十iy,它的实部与虚部同它的模与辐 角之间有如下的关系,一方面有 x=zcos Arg之,y=!zsin Arg z; 另一方面,反过来有 iz=+y. 从而有明显的不等式 1x|≤z|,{y|≤|z|,z|≤{x|+{yl
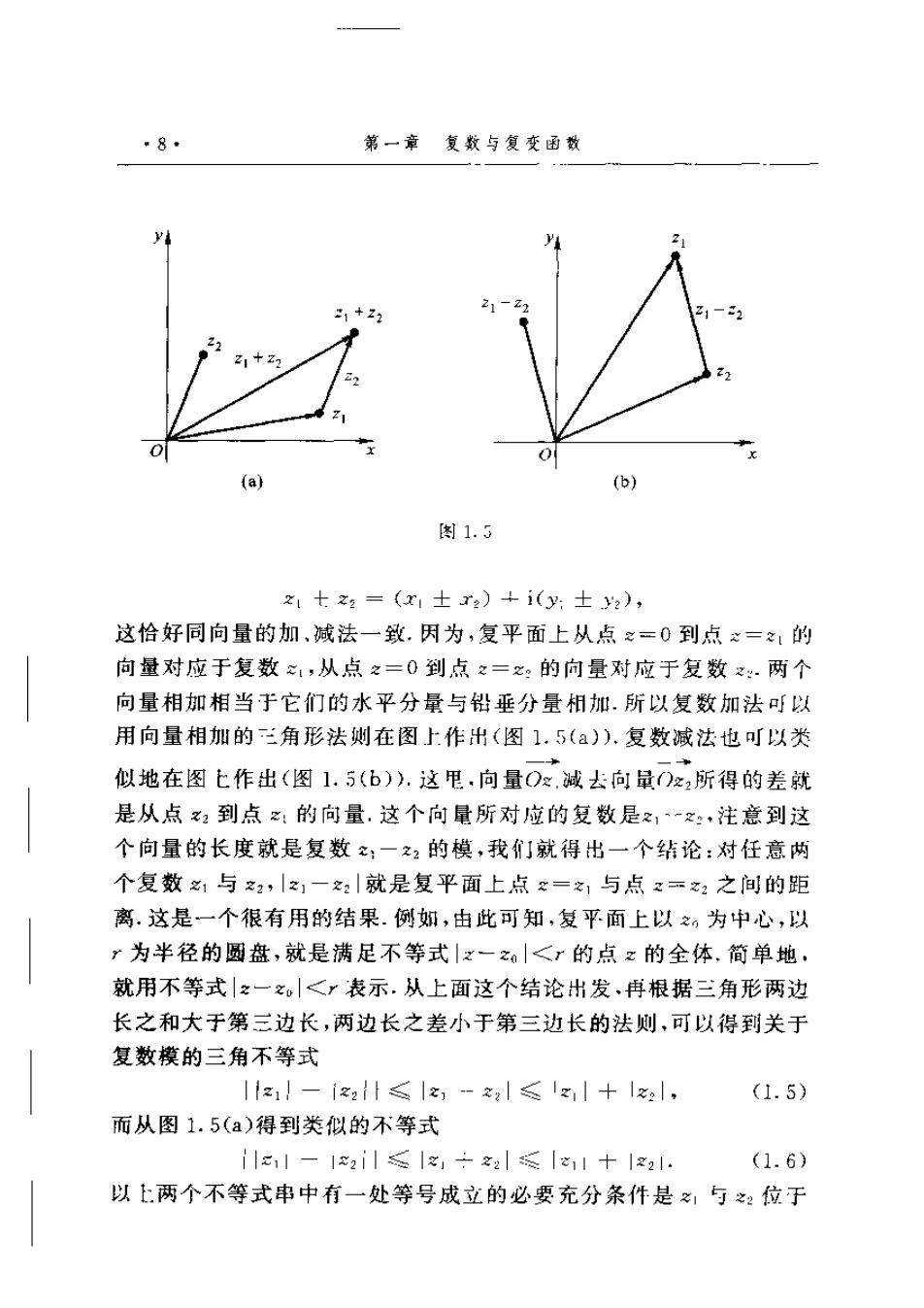
▣8 第一章复数与复变函数 2 1+2 (a) (b) 图1.5 z1tz=(x1士r2)+i(y:士y2), 这恰好同向量的加,减法一致.因为,复平面上从点之=0到点心=1的 向量对应于复数,从点之=0到点之=x。的向量对应于复数.两个 向量相加相当于它们的水平分量与铅垂分量相加.所以复数加法可以 用向量相加的三角形法则在图上作出(图1.5(a)).复数减法也可以类 似地在图飞作出(图1.5(b).这甩,向量Ox,减去向量)z2所得的差就 是从点2到点:的向量.这个向量所对应的复数是一,注意到这 个向量的长度就是复数之:一之2的模,我们就得出一个结论:对任意两 个复数之,与之2,之1一|就是复平面上点g=之1与点z=之2之间的距 离.这是一个很有用的结果.例如,由此可知,复平面上以,为中心,以 r为半径的圆盘,就是满足不等式|z一z|<r的点x的全体.简单地, 就用不等式z一之<y表示.从上面这个结论出发,再根据三角形两边 长之和大于第三边长,两边长之差小于第三边长的法则,可以得到关于 复数模的三角不等式 |1z1-i22l≤|z1-2|≤lz|+||, (1.5) 而从图1.5(a)得到类似的不等式 l11-12i||z1÷22||11十|21 (1.6) 以上两个不等式串中有一处等号成立的必要充分条件是,与位于