
3-8Fx=30+4(式中F的单位为N, 的单位为s)的合外力作用在质量m=10 kg 的物体上,试求:(1)在开始2s内此力的冲量:(2)若冲量/=300N-s,此力作用的时间;(3)若物体的初速度v=10m?s,方向与Fx相同,在1=6.86s时,此物体的速度02分析本题可由冲量的定义式I=Fdt,求变力的冲量,继而根据动量定理求物体的速度02解(1)由分析知1= J(30 + 4h)d = 301 +2 =68 N s(2)由/=300=301+2F,解此方程可得1=6.86s(另一解不合题意已舍去)(3)由动量定理,有1=m02-moi由(2)可知1=6.86s时1=300Ns,将1、m及0i代入可得 I+ mol =40 m-s-303-9高空作业时系安全带是非常必要的。假如一质量为51.0kg的人,在操作时不慎从高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来,已知此时人离原处的距离为2.0m,安全带弹性缓冲作用时间为0.50s:求安全带对人的平均冲力。分析从人受力的情况来看,可分两个阶段:在开始下落的过程中,只受重力作用,人体可看成是作自由落体运动;在安全带保护的缓冲过程中,则人体同时受重力和安全带冲力的作用,其合力是一变力,且作用时间很短。为求安全带的冲力,可以从缓冲时间内,人体运动状态(动量)的改变来分析,即运用动量定理来讨论。事实上,动量定理也可应用于整个过程。但是这时必须分清重力和安全带冲力作用的时间是不同的;而在过程的初态和末态,人体的速度均为零。这样,运用动量定理仍可得到相同的结果.解1以人为研究对象,按分析中的两个阶段进行讨论.在自由落体运动过程中,人跌落至2 m处时的速度为0 = /2gh()在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有(2)(F + P)t= m0, - mo)由式(1)、(2)可得安全带对人的平均冲力大小为4(mo) +A/2gh =1.14×10 NF=mg+=mgNtA解2从整个过程来讨论。根据动量定理有F=mg/2h/g+mg=1.14×10°N3-11如图所示,在水平地面上,有一横截面S=0.20m的直角弯管,管中有流速为u=
3 -8 Fx =30+4t(式中Fx 的单位为N,t 的单位为s)的合外力作用在质量m=10 kg 的物 体上,试求:(1) 在开始2s 内此力的冲量;(2) 若冲量I =300 N·s,此力作用的时间;(3) 若 物体的初速度v1 =10 m·s-1 ,方向与Fx 相同,在t=6.86s时,此物体的速度v2 . 分析 本题可由冲量的定义式 = 2 1 d t t I F t ,求变力的冲量,继而根据动量定理求物体的 速度v2. 解 (1) 由分析知 (30 4 )d 30 2 68 N s 2 0 2 2 0 = + = + = I t t t t (2) 由I =300 =30t +2t 2 ,解此方程可得 t =6.86 s(另一解不合题意已舍去) (3) 由动量定理,有 I =m v2- m v1 由(2)可知t =6.86 s 时I =300 N·s ,将I、m 及v1代入可得 1 1 2 40 m s − = + = m I mv v 3 -9 高空作业时系安全带是非常必要的.假如一质量为51.0 kg 的人,在操作时不慎从 高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来.已知此时人离原处的距离为2.0 m ,安全带弹性缓冲作用时间为0.50 s .求安全带对人的平均冲力. 分析 从人受力的情况来看,可分两个阶段:在开始下落的过程中,只受重力作用,人体可 看成是作自由落体运动;在安全带保护的缓冲过程中,则人体同时受重力和安全带冲力的作 用,其合力是一变力,且作用时间很短.为求安全带的冲力,可以从缓冲时间内,人体运动状态 (动量)的改变来分析,即运用动量定理来讨论.事实上,动量定理也可应用于整个过程.但是, 这时必须分清重力和安全带冲力作用的时间是不同的;而在过程的初态和末态,人体的速度 均为零.这样,运用动量定理仍可得到相同的结果. 解1 以人为研究对象,按分析中的两个阶段进行讨论.在自由落体运动过程中,人跌落至 2 m 处时的速度为 v1 = 2gh (1) 在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有 ( )Δ mv2 mv1 F + P t = − (2) 由式(1)、(2)可得安全带对人的平均冲力大小为 ( ) 1.14 10 N Δ Δ 2 Δ 3 = + = + = t gh mg t Δ m F mg v 解2 从整个过程来讨论.根据动量定理有 2 / 1.14 10 N Δ 3 = h g + mg = t mg F 3 -11 如图所示,在水平地面上,有一横截面S =0.20 m2 的直角弯管,管中有流速为v =

3.0ms的水通过,求弯管所受力的大小和方向题3-11图分析对于弯曲部分AB 段内的水而言,由于流速一定,在时间A1 内,从其一端流入的水量等于从另一端流出的水量.因此,对这部分水来说,在时间A1 内动量的增量也就是流入与流出水的动量的增量Ap=Am(B-0A):此动量的变化是管壁在Ai时间内对其作用冲量I的结果。依据动量定理可求得该段水受到管壁的冲力F;由牛顿第三定律,自然就得到水流对管壁的作用力F"=-F解在Ar时间内,从管一端流入(或流出)水的质量为Am =poSA,弯曲部分AB 的水的动量的增量则为Ap=Am(DB-DA) =pDSAI(UB-DA)依据动量定理I=Ap,得到管壁对这部分水的平均冲力F==SA(O-a)从而可得水流对管壁作用力的大小为F =-F=-V2pSb2 =-2.5x10 N作用力的方向则沿直角平分线指向弯管外侧。3-12一作斜抛运动的物体,在最高点炸裂为质量相等的两块,最高点距离地面为19.6m。爆炸1.00s后,第一块落到爆炸点正下方的地面上,此处距抛出点的水平距离为1.00×10m.问第二块落在距抛出点多远的地面上:(设空气的阻力不计)22题3-12图分析根据抛体运动规律,物体在最高点处的位置坐标和速度是易求的。因此,若能求出第二块碎片抛出的速度,按抛体运动的规律就可求得落地
3.0 m·s-1 的水通过,求弯管所受力的大小和方向. 分析 对于弯曲部分AB 段内的水而言,由于流速一定,在时间Δt 内,从其一端流入的水 量等于从另一端流出的水量.因此,对这部分水来说,在时间Δt 内动量的增量也就是流入与流 出水的动量的增量Δp=Δm(vB -vA );此动量的变化是管壁在Δt时间内对其作用冲量I 的结 果.依据动量定理可求得该段水受到管壁的冲力F;由牛顿第三定律,自然就得到水流对管壁 的作用力F′=-F. 解 在Δt 时间内,从管一端流入(或流出) 水的质量为Δm =ρυSΔt,弯曲部分AB 的水的 动量的增量则为 Δp=Δm(vB -vA ) =ρυSΔt (vB -vA ) 依据动量定理I =Δp,得到管壁对这部分水的平均冲力 ( ) B A ρS t t = = vΔ v − v Δ I F 从而可得水流对管壁作用力的大小为 2 2.5 10 N 2 3 F = −F = − ρSv = − 作用力的方向则沿直角平分线指向弯管外侧. 3 -12 一作斜抛运动的物体,在最高点炸裂为质量相等的两块,最高点距离地面为19.6 m.爆炸1.00 s 后,第一块落到爆炸点正下方的地面上,此处距抛出点的水平距离为1.00×102 m.问第二块落在距抛出点多远的地面上.(设空气的阻力不计) 分析 根据抛体运动规律,物体在最高点处的位置坐标和速度是易求的.因此,若能求出 第二块碎片抛出的速度,按抛体运动的规律就可求得落地

的位置。为此,分析物体在最高点处爆炸的过程,由于爆炸力属内力,且远大于重力,因此,重力的冲量可忽略,物体爆炸过程中应满足动量守恒。由于炸裂后第一块碎片抛出的速度可由落体运动求出,由动量守恒定律可得炸裂后第二块碎片抛出的速度,进一步求出落地位置解取如图示坐标,根据抛体运动的规律,爆炸前,物体在最高点A的速度的水平分量为-(1)物体爆炸后,第一块碎片竖直落下的运动方程为J=h-o1-,gt当该碎片落地时,有y=0,1=t,则由上式得爆炸后第一块碎片抛出的速度h-↓gi(2) U1=1又根据动量守恒定律,在最高点处有mOor==mO2(3)0=--mo,+mo2y(4)联立解式(1)、(2)、(3))和(4),可得爆炸后第二块碎片抛出时的速度分量分别为100m.s02x = 200x = 23h-igf=14.7m·s02, = 0f爆炸后,第二块碎片作斜抛运动,其运动方程为(5)X2=X +V22y=h+2y2-gt(6) 落地时,J2=0,由式(5)、(6)可解得第二块碎片落地点的水平位置x2 =500m*3-15一质量均匀柔软的绳竖直的悬挂着,绳的下端刚好触到水平桌面上.如果把绳的上端放开,绳将落在桌面上。试证明:在绳下落过程中的任意时刻,作用于桌面上的压力等于已落到桌面上绳的重量的三倍
的位置.为此,分析物体在最高点处爆炸的过程,由于爆炸力属内力,且远大于重力,因此, 重力的冲量可忽略,物体爆炸过程中应满足动量守恒.由于炸裂后第一块碎片抛出的速度可 由落体运动求出,由动量守恒定律可得炸裂后第二块碎片抛出的速度,进一步求出落地位置. 解 取如图示坐标,根据抛体运动的规律,爆炸前,物体在最高点A 的速度的水平分量为 h g x t x x 2 1 0 1 v0 = = (1) 物体爆炸后,第一块碎片竖直落下的运动方程为 2 1 1 2 1 y = h − v t − gt 当该碎片落地时,有y1 =0,t =t1 ,则由上式得爆炸后第一块碎片抛出的速度 1 2 1 2 1 t h − gt v = (2) 又根据动量守恒定律,在最高点处有 m 0x m 2x 2 1 v = v (3) m 1 m 2 y 2 1 2 1 0 = − v + v (4) 联立解式(1)、(2)、(3) 和(4),可得爆炸后第二块碎片抛出时的速度分量分别为 1 2 0 1 100 m s 2 2 2 − = = = h g x v x v x 1 1 2 1 2 1 14.7 m s 2 1 − = − = = t h gt v y v 爆炸后,第二块碎片作斜抛运动,其运动方程为 2 1 2 2 x x v t = + x (5) 2 2 2 2 2 2 1 y h t gt = + v y − (6) 落地时,y2 =0,由式(5)、(6)可解得第二块碎片落地点的水平位置 x2 =500 m *3 -15 一质量均匀柔软的绳竖直的悬挂着,绳的下端刚好触到水平桌面上.如果把绳的 上端放开,绳将落在桌面上.试证明:在绳下落过程中的任意时刻,作用于桌面上的压力等于 已落到桌面上绳的重量的三倍.
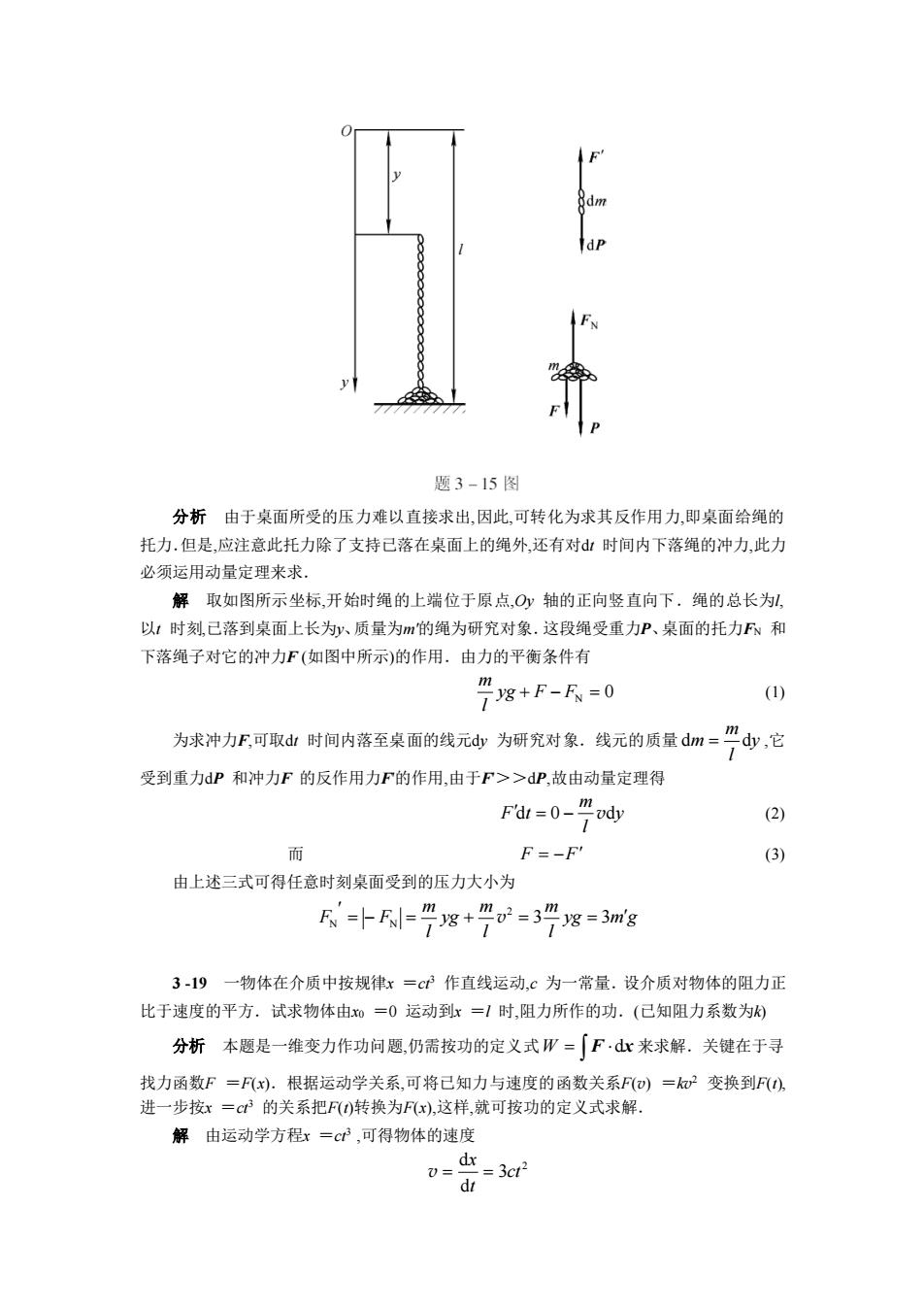
1aBanIdpFN题3-15图分析由于桌面所受的压力难以直接求出,因此,可转化为求其反作用力,即桌面给绳的托力.但是,应注意此托力除了支持已落在桌面上的绳外,还有对d时间内下落绳的冲力,此力必须运用动量定理来求.解取如图所示坐标,开始时绳的上端位于原点,Oy轴的正向竖直向下:绳的总长为1,以t时刻,已落到桌面上长为y、质量为m的绳为研究对象.这段绳受重力P、桌面的托力FN和下落绳子对它的冲力F(如图中所示)的作用:由力的平衡条件有F39+F-R,-0(1)为求冲力F,可取dt时间内落至桌面的线元dy为研究对象。线元的质量dm="dy,它受到重力dP 和冲力F 的反作用力F的作用,由于F>>dP,故由动量定理得F'dt=0-"ody(2) IF=-F(3)由上述三式可得任意时刻桌面受到的压力大小为F"=-F/-" yg+"0 =3"yg=3mg一物体在介质中按规律x=ci作直线运动,c为一常量.设介质对物体的阻力正3-19比于速度的平方。试求物体由xo=0运动到x=1时,阻力所作的功。(已知阻力系数为k)分析本题是一维变力作功问题,仍需按功的定义式W=『F·dx来求解。关键在于寻找力函数F=F(c)。根据运动学关系,可将已知力与速度的函数关系F(o)=ko变换到F(0),进一步按x=cF的关系把F(0)转换为F(x),这样,就可按功的定义式求解。解由运动学方程x=cF,可得物体的速度dx=3cf0=dt
分析 由于桌面所受的压力难以直接求出,因此,可转化为求其反作用力,即桌面给绳的 托力.但是,应注意此托力除了支持已落在桌面上的绳外,还有对dt 时间内下落绳的冲力,此力 必须运用动量定理来求. 解 取如图所示坐标,开始时绳的上端位于原点,Oy 轴的正向竖直向下.绳的总长为l, 以t 时刻,已落到桌面上长为y、质量为m′的绳为研究对象.这段绳受重力P、桌面的托力FN 和 下落绳子对它的冲力F (如图中所示)的作用.由力的平衡条件有 yg + F − FN = 0 l m (1) 为求冲力F,可取dt 时间内落至桌面的线元dy 为研究对象.线元的质量 y l m dm = d ,它 受到重力dP 和冲力F 的反作用力F′的作用,由于F′>>dP,故由动量定理得 y l m Fdt = 0 − vd (2) 而 F = −F (3) 由上述三式可得任意时刻桌面受到的压力大小为 yg m g l m l m yg l m F = − F = + = = 3 3 2 N N v 3 -19 一物体在介质中按规律x =ct3 作直线运动,c 为一常量.设介质对物体的阻力正 比于速度的平方.试求物体由x0 =0 运动到x =l 时,阻力所作的功.(已知阻力系数为k) 分析 本题是一维变力作功问题,仍需按功的定义式 W = F dx 来求解.关键在于寻 找力函数F =F(x).根据运动学关系,可将已知力与速度的函数关系F(v) =kv 2 变换到F(t), 进一步按x =ct3 的关系把F(t)转换为F(x),这样,就可按功的定义式求解. 解 由运动学方程x =ct3 ,可得物体的速度 2 3 d d ct t x v = =

按题意及上述关系,物体所受阻力的大小为F=ko2=9kctt=9kc2/34/3则阻力的功为27kc2137W=[F.dx W=I"F.dx=Jcos180°dx=-I'9kc/3/dx =-3-20一人从10.0m深的井中提水,起始桶中装有10.0kg的水,由于水桶漏水,每升高1.00m要漏去0.20kg的水。水桶被匀速地从井中提到井口,求所作的功.题3-20图分析由于水桶在匀速上提过程中,拉力必须始终与水桶重力相平衡。水桶重力因漏水而随提升高度而变,因此,拉力作功实为变力作功。由于拉力作功也就是克服重力的功,因此只要能写出重力随高度变化的关系,拉力作功即可题3-20图求出.解水桶在匀速上提过程中,α=0,拉力与水桶重力平衡,有F+P=0在图示所取坐标下,水桶重力随位置的变化关系为P =mg-agy其中α=0.2kg/m,人对水桶的拉力的功为W= [F-dy= [ (mg-agy)ly= 882 J3-26质量为m的地球卫星,沿半径为3Re的圆轨道运动,RE为地球的半径:已知地球的质量为mE。求:(1)卫星的动能;(2)卫星的引力势能;(3)卫星的机械能分析根据势能和动能的定义,只需知道卫星的所在位置和绕地球运动的速率,其势能和动能即可算出。由于卫星在地球引力作用下作圆周运动,由此可算得卫星绕地球运动的速率和动能,由于卫星的引力势能是属于系统(卫星和地球)的,要确定特定位置的势能时,必须规
按题意及上述关系,物体所受阻力的大小为 2 2 4 2 / 3 4 / 3 F = kv = 9kc t = 9kc x 则阻力的功为 W = F dx 4 / 3 2 / 3 7 / 3 0 2 / 3 0 7 27 W d cos 180 dx 9k c x dx k c l l o l = = = − = − F x 3 -20 一人从10.0 m 深的井中提水,起始桶中装有10.0 kg 的水,由于水桶漏水,每升高 1.00 m 要漏去0.20 kg 的水.水桶被匀速地从井中提到井口,求所作的功. 分析 由于水桶在匀速上提过程中,拉力必须始终与水桶重力相平衡.水桶重力因漏水 而随提升高度而变,因此,拉力作功实为变力作功.由于拉力作功也就是克服重力的功,因此, 只要能写出重力随高度变化的关系,拉力作功即可题3 -20 图求出. 解 水桶在匀速上提过程中,a =0,拉力与水桶重力平衡,有 F +P =0 在图示所取坐标下,水桶重力随位置的变化关系为 P =mg -αgy 其中α=0.2 kg/m,人对水桶的拉力的功为 d ( )d 882 J 10 0 0 = = − = W mg agy y l F y 3 -26 一质量为m 的地球卫星,沿半径为3RE 的圆轨道运动,RE 为地球的半径.已知地 球的质量为mE.求:(1) 卫星的动能;(2) 卫星的引力势能;(3) 卫星的机械能. 分析 根据势能和动能的定义,只需知道卫星的所在位置和绕地球运动的速率,其势能和 动能即可算出.由于卫星在地球引力作用下作圆周运动,由此可算得卫星绕地球运动的速率 和动能.由于卫星的引力势能是属于系统(卫星和地球)的,要确定特定位置的势能时,必须规