
11-8在双缝干涉实验中,两缝间距为0.30mm,用单色光垂直照射双缝,在离缝1.20m的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间的距离为22.78mm。问所用光的波长为多少,是什么颜色的光?分析与解在双缝干涉中,屏上暗纹位置由x=(2k+1)决定,式中α为双缝到屏的距离,d为双缝间距。所谓第5条暗纹是指对应k=4的那一级暗纹。由于条纹对称,2278mm,那么由暗纹公式即可求得波长。此外,因该暗纹到中央明纹中心的距离x=入求入射光波长.应注意两个第5条双缝干涉是等间距的,故也可用条纹间距公式Ax略纹之间所包合的相邻条纹间隔数为9(不是10,为什么?),故Ax=278mm。号,把k=4x=278×10-m以及d、值代解1屏上暗纹的位置x=%(2k+1),入,可得1=632.8nm,为红光解 2 屏上相暗较(或明纹)间距Ax=%元,把Ax-2,×10-m,以及 d、d值代入,可得入=632.8nm.11-9在双缝干涉实验中,用波长入=546.1mm的单色光照射,双缝与屏的距离d=300mm,测得中央明纹两侧的两个第五级明条纹的间距为12.2mm,求双缝间的距离分析双缝干涉在屏上形成的条纹是上下对称且等间隔的。如果设两明纹间隔为Ar,则由中央明纹两侧第五级明纹间距xs-xs=10Ax可求出Ar.再由公式Ar=da/d即可求出双缝间距d.解根据分析:Ar=(xsxs)/10=1.22×103m双缝间距:d =d^ / Ar =1.34×104m11-10一个微波发射器置于岸上,离水面高度为d,对岸在离水面h高度处放置一接收器,水面宽度为D,且D》d,D》h,如图所示。发射器向对面发射波长为入的微波,且入>d,求接收器测到极大值时,至少离地多高?分析由发射器直接发射的微波与经水面反射后的微波相遇可互相干涉,这种干涉与劳埃德镜实验完全相同。形成的干涉结果与缝距为2d,缝屏间距为D的双缝干涉相似,如图(b)所示,但要注意的是和劳埃德镜实验一样,由于从水面上反射的光存在半波损失,使得两束光在屏上相遇产生的光程差为2dsinO+入/2,而不是2dsino
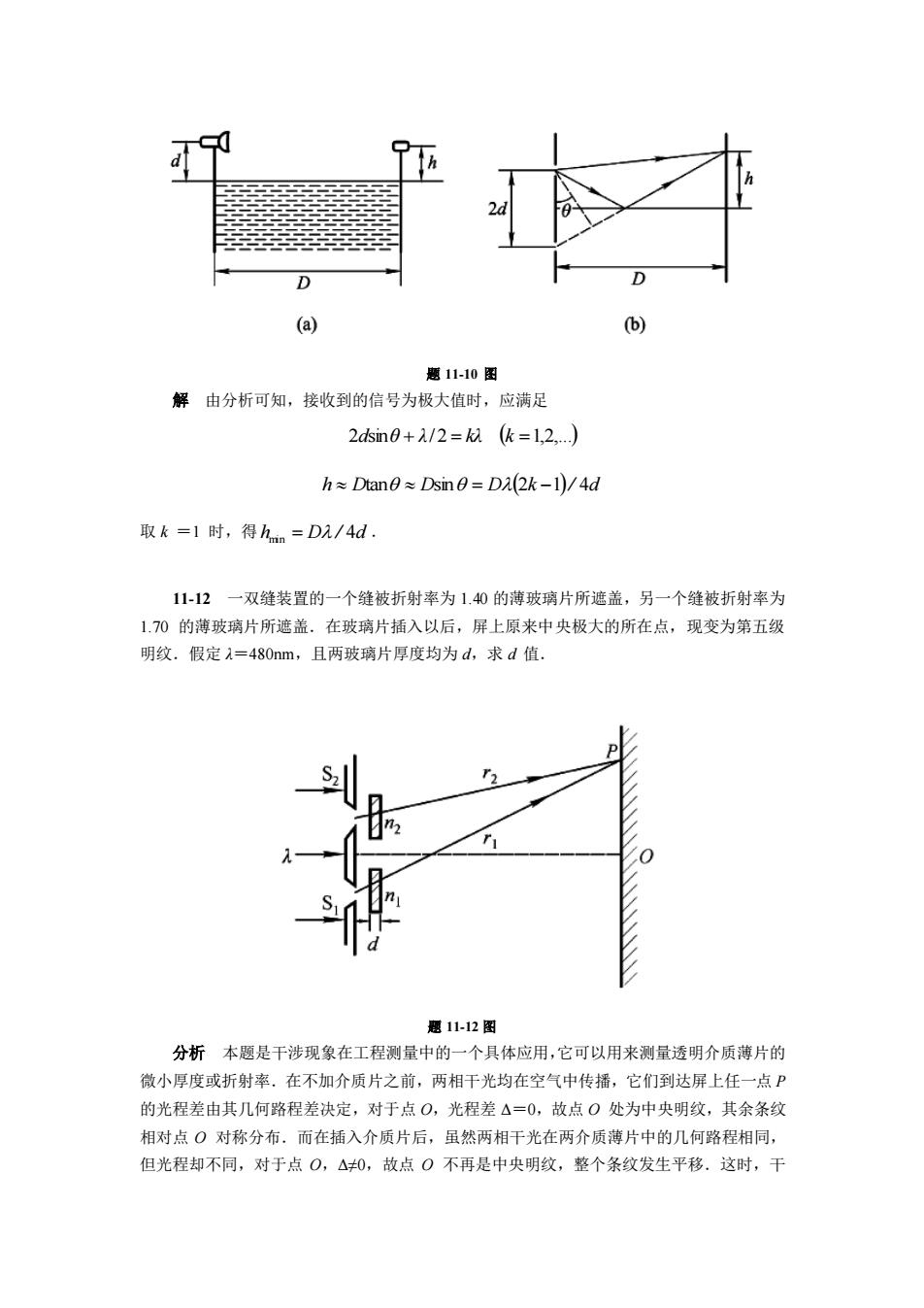
11-8 在双缝干涉实验中,两缝间距为 0.30 mm,用单色光垂直照射双缝,在离缝 1.20m 的屏上测得中央明纹一侧第 5 条暗纹与另一侧第 5 条暗纹间的距离为 22.78 mm.问所用光 的波长为多少,是什么颜色的光? 分析与解 在双缝干涉中,屏上暗纹位置由 ( ) 2 2 1 + = k d d x 决定,式中 d′为双缝到 屏的距离,d 为双缝间距.所谓第 5 条暗纹是指对应 k =4 的那一级暗纹.由于条纹对称, 该暗纹到中央明纹中心的距离 mm 2 22.78 x = ,那么由暗纹公式即可求得波长 λ.此外,因 双缝干涉是等间距的,故也可用条纹间距公式 d d x = 求入射光波长.应注意两个第 5 条 暗纹之间所包含的相邻条纹间隔数为 9(不是 10,为什么?),故 mm 9 22.78 x = 。 解 1 屏上暗纹的位置 ( ) 2 2 1 + = k d d x ,把 10 m 2 22 78 4 −3 = = . k ,x 以及 d、d′值代 入,可得 λ=632.8 nm,为红光. 解 2 屏上相邻暗纹(或明纹)间距 ' d x d = ,把 22.78 3 10 m 9 x − = ,以及 d、d′ 值代入,可得 λ=632.8 nm. 11-9 在双缝干涉实验中,用波长 λ=546.1 nm 的单色光照射,双缝与屏的距离 d′= 300mm.测得中央明纹两侧的两个第五级明条纹的间距为 12.2mm,求双缝间的距离. 分析 双缝干涉在屏上形成的条纹是上下对称且等间隔的.如果设两明纹间隔为 Δx, 则由中央明纹两侧第五级明纹间距 x5 -x-5 =10Δx 可求出 Δx.再由公式 Δx =d′λ/d 即可 求出双缝间距 d. 解 根据分析:Δx =(x5 -x-5)/10 =1.22×10-3 m 双缝间距: d =d′λ/Δx =1.34 ×10-4 m 11-10 一个微波发射器置于岸上,离水面高度为 d,对岸在离水面 h 高度处放置一接 收器,水面宽度为 D,且 D d D h , ,如图所示.发射器向对面发射波长为 λ 的微波, 且 λ>d,求接收器测到极大值时,至少离地多高? 分析 由发射器直接发射的微波与经水面反射后的微波相遇可互相干涉,这种干涉与劳 埃德镜实验完全相同.形成的干涉结果与缝距为 2d,缝屏间距为 D 的双缝干涉相似,如图 (b)所示,但要注意的是和劳埃德镜实验一样,由于从水面上反射的光存在半波损失,使 得两束光在屏上相遇产生的光程差为 2dsinθ + λ/2 ,而不是 2dsinθ .
YRTh鑫DD(a)(b) 题 11-10 图解由分析可知,接收到的信号为极大值时,应满足2dsin+^/2= ka (k=1,2..)h ~ Dtan ~ Dsin Q = Da(2k -1)/ 4d 取k=1 时,得hm=Da/4d.11-12一双缝装置的一个缝被折射率为1.40的薄玻璃片所遮盖,另一个缝被折射率为1.70的薄玻璃片所遮盖,在玻璃片插入以后,屏上原来中央极大的所在点,现变为第五级明纹,假定入=480nm,且两玻璃片厚度均为d,求d值题 11-12 图分析本题是干涉现象在工程测量中的一个具体应用,它可以用来测量透明介质薄片的微小厚度或折射率。在不加介质片之前,两相干光均在空气中传播,它们到达屏上任一点P的光程差由其几何路程差决定,对于点O,光程差A=0,故点O处为中央明纹,其余条纹相对点○对称分布。而在插入介质片后,虽然两相干光在两介质薄片中的几何路程相同,但光程却不同,对于点O,#0,故点0不再是中央明纹,整个条纹发生平移。这时,干
题 11-10 图 解 由分析可知,接收到的信号为极大值时,应满足 2dsinθ + λ/2 = kλ (k =1,2,.) h Dtan Dsin = D(2k −1)/ 4d 取 k =1 时,得 hmin = D / 4d . 11-12 一双缝装置的一个缝被折射率为 1.40 的薄玻璃片所遮盖,另一个缝被折射率为 1.70 的薄玻璃片所遮盖.在玻璃片插入以后,屏上原来中央极大的所在点,现变为第五级 明纹.假定 λ=480nm,且两玻璃片厚度均为 d,求 d 值. 题 11-12 图 分析 本题是干涉现象在工程测量中的一个具体应用,它可以用来测量透明介质薄片的 微小厚度或折射率.在不加介质片之前,两相干光均在空气中传播,它们到达屏上任一点 P 的光程差由其几何路程差决定,对于点 O,光程差 Δ=0,故点 O 处为中央明纹,其余条纹 相对点 O 对称分布.而在插入介质片后,虽然两相干光在两介质薄片中的几何路程相同, 但光程却不同,对于点 O,Δ≠0,故点 O 不再是中央明纹,整个条纹发生平移.这时,干

涉条纹空间分布的变化完全取决于光程差的变化,因此,对于屏上某点P(明纹或暗纹位置只要计算出插入介质片前后光程差的变化,即可知道其干涉条纹的变化情况.插入介质前的光程差A=n—r2=kia(对应ki级明纹),插入介质后的光程差 A2(m-1)d+n]-[(m2-1)d+]=k(对应k级明纹).光程差的变化量为=(kz-k)d式中(k2一k)可以理解为移过点P的条纹数(本题为5)因此,对于这类问题,求解光程差的变化量是解题的关键解由上述分析可知,两介质片插入前后,对于原中央明纹所在点O,有4,-A,=(n -n)d=52将有关数据代入可得28.0 μmn,-n.11-14在折射率ns=1.52的照相机镜头表面涂有一层折射率m2=1.38的MgF2增透膜,若此膜仅适用于波长入=550nm的光,则此膜的最小厚度为多少2分析在薄膜干涉中,膜的材料及厚度都将对两反射光(或两透射光)的光程差产生影响,从而可使某些波长的光在反射(或透射)中得到加强或减弱,这种选择性使薄膜干涉在工程技术上有很多应用.本题所述的增透膜,就是希望波长入=550nm的光在透射中得到加强,从而得到所希望的照相效果(因感光底片对此波长附近的光最为敏感),具体求解时应注意在d>0的前提下,k取最小的允许值,解1因干涉的互补性,波长为550nm的光在透射中得到加强,则在反射中一定减弱,两反射光的光程差42=2m2d,由干涉相消条件△z=(2k+1),得d=@k+1)/m取k=0,则dmin=99.6nm解2由于空气的折射率ni=1,且有m<n2<ns,则对透射光而言,两相干光的光程差△,=2n,d+,由干涉加强条件A=k,得d=(2k+1) 4n取k=1,则膜的最小厚度dmin=99.6nm.11-15利用空气劈尖测细丝直径.如图所示,已知1=589.3nm,=2.888×10-2m测得30条条纹的总宽度为4.259×10m,求细丝直径d
涉条纹空间分布的变化完全取决于光程差的变化.因此,对于屏上某点 P(明纹或暗纹位置), 只要计算出 插入介质片前后光程差的变化,即可知道其干涉条纹的变化情况. 插入介质前的光程差 Δ1 =r1 -r 2 =k1 (对应 λ k1 级明纹),插入介质后的光程差 Δ2 = [(n1-1)d +r1 ]-[(n2 -1)d +r2 ]=k2 λ(对应 k2 级明纹).光程差的变化量为 Δ2 -Δ1 =(n2 -n1 )d =(k2 -k1 )λ 式中(k2 -k1 )可以理解为移过点 P 的条纹数(本题为 5).因此,对于这类问题,求解 光程差的变化量是解题的关键. 解 由上述分析可知,两介质片插入前后,对于原中央明纹所在点 O,有 2 − 1 = (n2 − n1 )d = 5 将有关数据代入可得 8 0 μm 5 2 1 = . − = n n d 11-14 在折射率 n3 =1.52 的照相机镜头表面涂有一层折射率 n2 =1.38 的 MgF2 增透 膜,若此膜仅适用于波长 λ=550nm 的光,则此膜的最小厚度为多少? 分析 在薄膜干涉中,膜的材料及厚度都将对两反射光(或两透射光)的光程差产生影 响,从而可使某些波长的光在反射(或透射)中得到加强或减弱,这种选择性使薄膜干涉在 工程技术上有很多应用.本题所述的增透膜,就是希望波长 λ=550nm 的光在透射中得到加 强,从而得到所希望的照相效果(因感光底片对此波长附近的光最为敏感).具体求解时应 注意在 d>0 的前提下,k 取最小的允许值. 解 1 因干涉的互补性,波长为 550nm 的光在透射中得到加强,则在反射中一定减弱, 两反射光的光程差 Δ2 =2n2 d,由干涉相消条件 ( ) 2 2 2 1 = k + ,得 ( ) 4 2 2 1 n d k = + 取 k =0,则 dmin =99.6nm. 解 2 由于空气的折射率 n1 =1,且有 n1 <n2 <n3 ,则对透射光而言,两相干光的 光程差 2 1 2 2 = n d + ,由干涉加强条件 Δ1 =kλ,得 ( ) 4 2 2 1 n d k = + 取 k =1,则膜的最小厚度 dmin =99.6nm. 11-15 利用空气劈尖测细丝直径.如图所示,已知 λ=589.3 nm,L =2.888 ×10-2m, 测得 30 条条纹的总宽度为 4.259 ×10-3 m,求细丝直径 d.

分析在应用劈尖干涉公式d=2%L时,应注意相邻条纹的间距b是N条条纹的宽度Ax除以(N-1):对空气劈尖n解“由分析知,相邻条纹间距b-:则细丝直径为N2(N-1 =5.75x×10~ md :T2nb2nAr题 11-15 图11—20在利用牛顿环测未知单色光波长的实验中,当用已知波长为589.3nm的钠黄光垂直照射时,测得第一和第四暗环的距离为Ar4.00×10-3m:当用波长未知的单色光重直照射时,测得第一和第四暗环的距离为Ar=3.85×10m,求该单色光的波长,分析牛顿环装置产生的干涉暗环半径r=VkR,其中k=0,1,2..,k=0,对应牛顿环中心的暗斑,k=1和K=4则对应第一和第四暗环,由它们之间的间距Ar=-=R,可知rαV,据此可按题中的测量方法求出未知波长"解根据分析有Ar*"=546 nm故未知光波长11-21在牛顿环实验中,当透镜与玻璃之间充以某种液体时,第10个亮环的直径由1.40×10-2m变为 1.27×10-2m,试求这种液体的折射率分析 当透镜与平板玻璃间充满某种液体(m2 >1),且满足 ml >m2 ,m2 <m 或 m<m>m时,在厚度为d的地方,两相干光的光程差为△=2n,d+·由此可推导出牛顿M和明环半径r=1R,这里明、暗环半径和充入的介质折环暗环半径r=Yn,2射率 n2有关。有兴趣的读者可自行推导。必须指出,在牛顿环中,若介质不均匀或分析的是透射光而不是反射光,那么关于暗环、明环半径的公式与教材中的公式是不同的,不能随意套用。解当透镜与玻璃之间为空气时,k级明纹的直径为
分析 在应用劈尖干涉公式 L nb d 2 = 时,应注意相邻条纹的间距 b 是 N 条条纹的 宽度 Δx 除以(N -1).对空气劈尖 n =1. 解 由分析知,相邻条纹间距 −1 = N x b ,则细丝直径为 ( ) 5 75 10 m 2 1 2 −5 = − = = . n x N L nb d 题 11-15 图 11 -20 在利用牛顿环测未知单色光波长的实验中,当用已知波长为 589.3 nm 的钠黄 光垂直照射时,测得第一和第四暗环的距离为 Δr =4.00 ×10-3 m;当用波长未知的单色光垂 直照射时,测得第一和第四暗环的距离为 Δr′=3.85 ×10-3 m,求该单色光的波长. 分析 牛顿环装置产生的干涉暗环半径 r = kR ,其中 k =0,1,2.,k =0,对应 牛顿环中心的暗斑,k=1 和 k =4 则对应第一和第四暗环,由它们之间的间距 r = r4 − r1 = R ,可知 r ,据此可按题中的测量方法求出未知波长 λ′. 解 根据分析有 = r r 故未知光波长 λ′=546 nm 11-21 在牛顿环实验中,当透镜与玻璃之间充以某种液体时,第 10 个亮环的直径由 1.40×10-2 m 变为 1.27 ×10-2 m,试求这种液体的折射率. 分析 当透镜与平板玻璃间充满某种液体(n2 >1),且满足 n1 >n2 ,n2 <n3 或 n1 <n2 , n2 >n3 时,在厚度为 d 的地方,两相干光的光程差为 2 2 2 = n d + .由此可推导出牛顿 环暗环半径 n2 kR r = 和明环半径 2 2 1 n R r k = − ,这里明、暗环半径和充入的介质折 射率 n2 有关.有兴趣的读者可自行推导.必须指出,在牛顿环中,若介质不均匀或分析的 是透射光而不是反射光,那么关于暗环、明环半径的公式与教材中的公式是不同的,不能随 意套用. 解 当透镜与玻璃之间为空气时,k 级明纹的直径为

d,=2r,=2k-R当透镜与玻璃之间为液体时,k级明纹的直径1RAd,=2r,=222解上述两式得(4) =1.22n=d11-23把折射率n=1.40的薄膜放入迈克耳孙干涉仪的一臂,如果由此产生了7.0条条纹的移动,求膜厚。设入射光的波长为589nm分析迈克耳孙干涉仪中的干涉现象可以等效为薄膜干涉(两平面镜相互垂直)和劈尖干涉(两平面镜不垂直)两种情况,本题属于后一种情况.在干涉仪一臂中插入介质片后两束相干光的光程差改变了,相当于在观察者视野内的空气劈尖的厚度改变了,从而引起干涉条纹的移动.解插入厚度为d的介质片后,两相干光光程差的改变量为2(n-1)d,从而引起N条条纹的移动,根据劈尖干涉加强的条件,有2(n-1)d=Na,得d=NaNad=2/n-1=5.154x10-°m11-24如图所示,狭缝的宽度b=0.60mm,透镜焦距=0.40m,有一与狭缝平行的屏放置在透镜焦平面处,若以单色平行光垂直照射狭缝,则在屏上离点O为x=1.4mm处的点P,看到的是衍射明条纹。试求:(1)该入射光的波长:(2)点P条纹的级数:(3)从点P看来对该光波而言,狭缝处的波阵面可作半波带的数目分析单缝衍射中的明纹条件为bsing=(2k+1),在观察点P确定(即确定)后,由于k只能取整数值,故满足上式的入只可取若干不连续的值,对照可见光的波长范围可确定入射光波长的取值,此外,如点P处的明纹级次为k,则狭缝处的波阵面可以划分的半波带数目为(2k+1),它们都与观察点P有关,越大,可以划分的半波带数目也越大。.根据单缝衍解(1)透镜到屏的距离为d,由于d>>b,对点P而言,有sinβ~射明纹条件bsing=(2k+1)=,有等=2k+哈1将b、d(d-p)、x的值代入,并考虑可见光波长的上、下限值,有
dk rk k R = = − 2 1 2 2 当透镜与玻璃之间为液体时,k 级明纹的直径为 2 2 1 2 2 R d r k k k = = − 解上述两式得 1 22 2 2 = . = k k d d n 11-23 把折射率 n =1.40 的薄膜放入迈克耳孙干涉仪的一臂,如果由此产生了 7.0 条 条纹的移动,求膜厚.设入射光的波长为 589 nm. 分析 迈克耳孙干涉仪中的干涉现象可以等效为薄膜干涉(两平面镜相互垂直)和劈尖 干涉(两平面镜不垂直)两种情况,本题属于后一种情况.在干涉仪一臂中插入介质片后, 两束相干光的光程差改变了,相当于在观察者视野内的空气劈尖的厚度改变了,从而引起干 涉条纹的移动. 解 插入厚度为 d 的介质片后,两相干光光程差的改变量为 2(n -1)d,从而引起 N 条条纹的移动,根据劈尖干涉加强的条件,有 2(n -1)d=Nλ,得 d= Nλ ( ) 5 154 10 m 2 1 −6 = − = . n N d 11-24 如图所示,狭缝的宽度 b =0.60 mm,透镜焦距 f =0.40m,有一与狭缝平行的 屏放置在透镜焦平面处.若以单色平行光垂直照射狭缝,则在屏上离点 O 为 x =1.4 mm 处 的点 P,看到的是衍射明条纹.试求:(1) 该入射光的波长;(2) 点 P 条纹的级数;(3) 从点 P 看来对该光波而言,狭缝处的波阵面可作半波带的数目. 分析 单缝衍射中的明纹条件为 ( ) 2 sin 2 1 b = k + ,在观察点 P 确定(即 φ 确定) 后,由于 k 只能取整数值,故满足上式的 λ 只可取若干不连续的值,对照可见光的波长范 围可确定入射光波长的取值.此外,如点 P 处的明纹级次为 k,则狭缝处的波阵面可以划 分的半波带数目为(2k +1),它们都与观察点 P 有关,φ 越大,可以划分的半波带数目 也越大. 解 (1) 透镜到屏的距离为 d,由于 d >>b,对点 P 而言,有 d x sin .根据单缝衍 射明纹条件 ( ) 2 sin 2 1 b = k + ,有 ( ) 2 2 1 = k + d bx 将 b、d(d≈f)、x 的值代入,并考虑可见光波长的上、下限值,有