
4一10如图(a)所示,圆盘的质量为m,半径为R.求:(1)以O为中心,将半径为R/2的部分挖去,剩余部分对0O轴的转动惯量:(2)剩余部分对OO轴(即通过圆盘边缘且平行于盘中心轴)的转动惯量O.(b)(a)题4-10图分析由于转动惯量的可加性,求解第一问可有两种方法:一是由定义式J=「r~dm计算,式中dm可取半径为r、宽度为dr窄圆环;二是用补偿法可将剩余部分的转动惯量看成是原大圆盘和挖去的小圆盘对同一轴的转动惯量的差值。至于第二问需用到平行轴定理解挖去后的圆盘如图(b)所示。(1)解1由分析知Jo- ram-r最2mdr-rar-0mR解2整个圆盘对00轴转动惯量为J,mR2,挖去的小圆盘对00轴转动惯量2RmR2,由分析知,剩余部分对00轴的转动惯量为元R2元2J =J,-J2=-10mR?(2)由平行轴定理,乘剩余部分对00轴的转动惯量为Jo=号mR+m-()]-号m元一4-11用落体观察法测定飞轮的转动惯量,是将半径为R的飞轮支承在O点上,然后在绕过飞轮的绳子的一端挂一质量为m的重物,令重物以初速度为零下落,带动飞轮转动(如图)。记下重物下落的距离和时间,就可算出飞轮的转动惯量。试写出它的计算式。(假设轴
4 -10 如图(a)所示,圆盘的质量为m,半径为R.求:(1) 以O为中心,将半径为R/2 的 部分挖去,剩余部分对OO 轴的转动惯量;(2) 剩余部分对O′O′轴(即通过圆盘边缘且平行 于盘中心轴)的转动惯量. 分析 由于转动惯量的可加性,求解第一问可有两种方法:一是由定义式 J r dm 2 = 计算, 式中dm 可取半径为r、宽度为dr 窄圆环;二是用补偿法可将剩余部分的转动惯量看成是原 大圆盘和挖去的小圆盘对同一轴的转动惯量的差值.至于第二问需用到平行轴定理. 解 挖去后的圆盘如图(b)所示. (1) 解1 由分析知 2 / 2 3 2 2 / 2 2 2 0 32 15 d 2 2π d π d r r mR R m r r R m J r m r R R R R = = = = 解2 整个圆盘对OO 轴转动惯量为 2 1 2 1 J = mR ,挖去的小圆盘对OO 轴转动惯量 2 2 2 2 2 32 1 2 2 π 2 π 1 mR R R R m J = = ,由分析知,剩余部分对OO 轴的转动惯量为 2 0 1 2 32 15 J = J − J = mR (2) 由平行轴定理,剩余部分对O′O′轴的转动惯量为 2 2 2 2 2 0 32 39 2 π 32 π 15 R mR R R m J mR m = = + − 4 -11 用落体观察法测定飞轮的转动惯量,是将半径为R 的飞轮支承在O点上,然后在绕 过飞轮的绳子的一端挂一质量为m 的重物,令重物以初速度为零下落,带动飞轮转动(如 图).记下重物下落的距离和时间,就可算出飞轮的转动惯量.试写出它的计算式.(假设轴

承间无摩擦)。题4-11图分析在运动过程中,飞轮和重物的运动形式是不同的。飞轮作定轴转动,而重物是作落体运动,它们之间有着内在的联系。由于绳子不可伸长,并且质量可以忽略。这样,飞轮的转动惯量,就可根据转动定律和牛顿定律联合来确定,其中重物的加速度,可通过它下落时的匀加速运动规律来确定.该题也可用功能关系来处理。将飞轮、重物和地球视为系统,绳子张力作用于飞轮、重物的功之和为零,系统的机械能守恒。利用匀加速运动的路程、速度和加速度关系,以及线速度和角速度的关系,代入机械能守恒方程中即可解得,解1设绳子的拉力为Ft,对飞轮而言,根据转动定律,有()FR=Ja而对重物而言,由牛顿定律,有(2) mg-F,=ma由于绳子不可伸长,因此,有(3)α= Rα重物作匀加速下落,则有h=jar?(4)由上述各式可解得飞轮的转动惯量为gtJ =mR2h解2根据系统的机械能守恒定律,有+Jo=0(1)-mgh+而线速度和角速度的关系为0= Ro(2) 又根据重物作匀加速运动时,有0=at(3)
承间无摩擦). 分析 在运动过程中,飞轮和重物的运动形式是不同的.飞轮作定轴转动,而重物是作落体 运动,它们之间有着内在的联系.由于绳子不可伸长,并且质量可以忽略.这样,飞轮的转 动惯量,就可根据转动定律和牛顿定律联合来确定,其中重物的加速度,可通过它下落时的 匀加速运动规律来确定. 该题也可用功能关系来处理.将飞轮、重物和地球视为系统,绳子张力作用于飞轮、重 物的功之和为零,系统的机械能守恒.利用匀加速运动的路程、速度和加速度关系,以及线 速度和角速度的关系,代入机械能守恒方程中即可解得. 解1 设绳子的拉力为FT,对飞轮而言,根据转动定律,有 FTR = Jα (1) 而对重物而言,由牛顿定律,有 mg − FT = ma (2) 由于绳子不可伸长,因此,有 a = Rα (3) 重物作匀加速下落,则有 2 2 1 h = at (4) 由上述各式可解得飞轮的转动惯量为 = −1 2 2 2 h gt J mR 解2 根据系统的机械能守恒定律,有 0 2 1 2 1 2 2 − mgh + mv + Jω = (1′) 而线速度和角速度的关系为 v = Rω (2′) 又根据重物作匀加速运动时,有 v = at (3′)
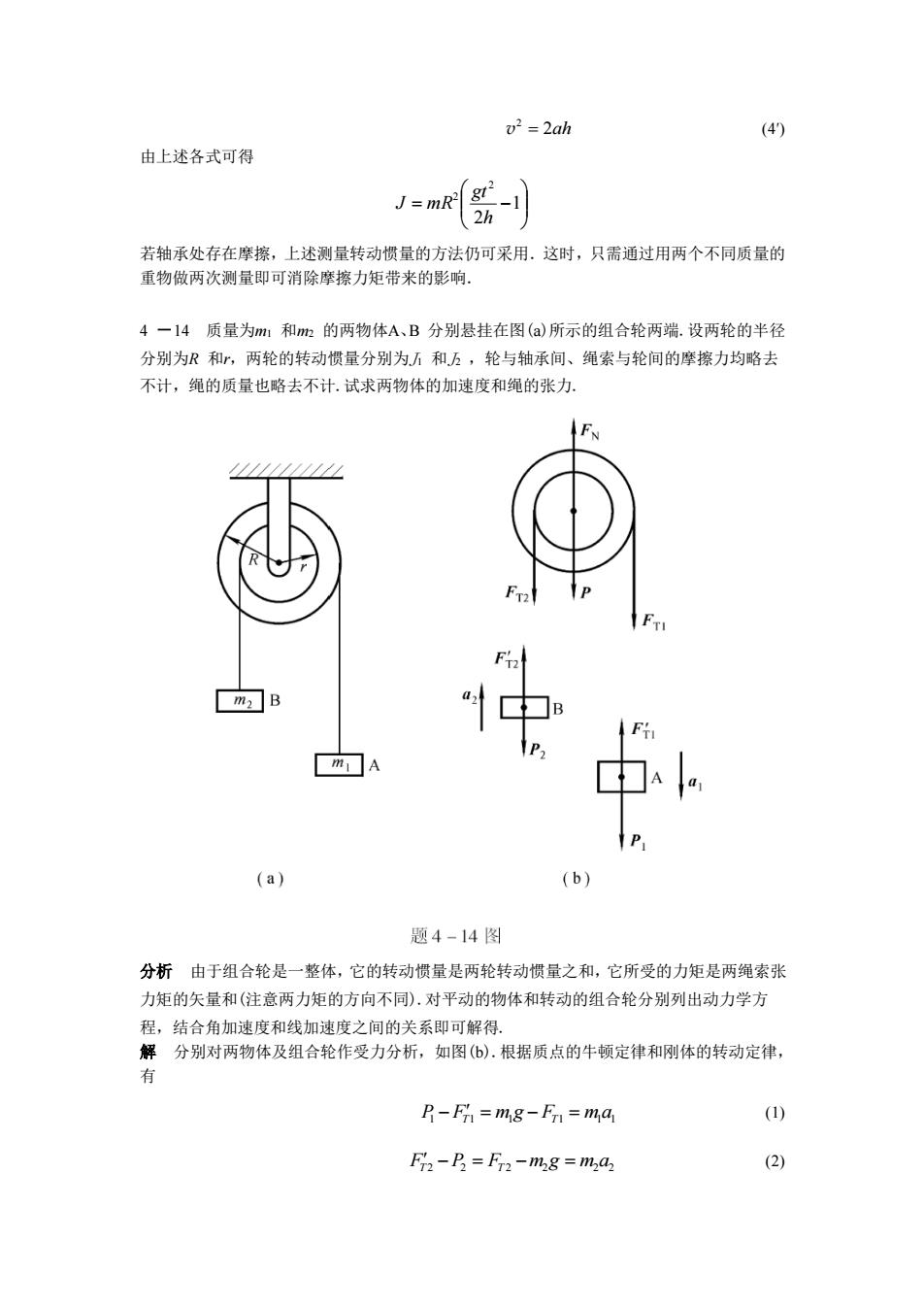
0?=2ah(4)由上述各式可得g=mR2h若轴承处存在摩擦,上述测量转动惯量的方法仍可采用。这时,只需通过用两个不同质量的重物做两次测量即可消除摩擦力矩带来的影响4-14质量为ml和m2的两物体A、B分别悬挂在图(a)所示的组合轮两端.设两轮的半径分别为R和r,两轮的转动惯量分别为万和.,轮与轴承间、绳索与轮间的摩擦力均略去不计,绳的质量也略去不计.试求两物体的加速度和绳的张力。FNAFf2中mBFTAA(a)(b)题4-14图分析由于组合轮是一整体,它的转动惯量是两轮转动惯量之和,它所受的力矩是两绳索张力矩的矢量和(注意两力矩的方向不同).对平动的物体和转动的组合轮分别列出动力学方程,结合角加速度和线加速度之间的关系即可解得。解分别对两物体及组合轮作受力分析,如图(b).根据质点的牛顿定律和刚体的转动定律,有()P-Fr=mg-Fr=mai(2)Ff2-P = Ff2 -mg = ma2
2ah 2 v = (4′) 由上述各式可得 = −1 2 2 2 h gt J mR 若轴承处存在摩擦,上述测量转动惯量的方法仍可采用.这时,只需通过用两个不同质量的 重物做两次测量即可消除摩擦力矩带来的影响. 4 -14 质量为m1 和m2 的两物体A、B 分别悬挂在图(a)所示的组合轮两端.设两轮的半径 分别为R 和r,两轮的转动惯量分别为J1 和J2 ,轮与轴承间、绳索与轮间的摩擦力均略去 不计,绳的质量也略去不计.试求两物体的加速度和绳的张力. 分析 由于组合轮是一整体,它的转动惯量是两轮转动惯量之和,它所受的力矩是两绳索张 力矩的矢量和(注意两力矩的方向不同).对平动的物体和转动的组合轮分别列出动力学方 程,结合角加速度和线加速度之间的关系即可解得. 解 分别对两物体及组合轮作受力分析,如图(b).根据质点的牛顿定律和刚体的转动定律, 有 P1 FT1 = m1g − FT1 = m1a1 − (1) FT 2 −P2 = FT 2 −m2g = m2a2 (2)

(3)FnR-Frar=(I+J,)aFr = Fn,Ff2 = Fr2(4)由角加速度和线加速度之间的关系,有α = Rα(5) a, =ra(6)解上述方程组,可得m,R-m,ra="J+J.+mR+m,rgRm,R-m,J,+J+mR+mrJ+J.+mr?+mRJ+J,+mR+mrJ+J,+mR+mRFr2:m.gJ.+J,+m,R+mr24一18如图所示,一通风机的转动部分以初角速度oo绕其轴转动,空气的阻力矩与角速度成正比,比例系数C为一常量.若转动部分对其轴的转动惯量为J,间:(1)经过多少时间后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转?题4-18图分析由于空气的阻力矩与角速度成正比,由转动定律可知,在变力矩作用下,通风机叶片的转动是变角加速转动,因此,在讨论转动的运动学关系时,必须从角加速度和角速度的定义出发,通过积分的方法去解。解(1)通风机叶片所受的阻力矩为M=-C,由转动定律M=Jα,可得叶片的角加速度为
FT1R− FT 2 r = (J1 + J2 )α (3) FT1 = FT1 , FT 2 = FT 2 (4) 由角加速度和线加速度之间的关系,有 a1 = Rα (5) a2 = rα (6) 解上述方程组,可得 gR J J m R m r m R m r a 2 2 2 1 2 1 1 2 1 + + + − = gr J J m R m r m R m r a 2 2 2 1 2 1 1 2 2 + + + − = m g J J m R m r J J m r m Rr FT 2 1 2 2 1 2 1 2 2 1 2 1 1 + + + + + + = m g J J m R m r J J m R m Rr FT 2 2 2 2 1 2 1 1 2 1 2 1 2 + + + + + + = 4 -18 如图所示,一通风机的转动部分以初角速度ω0 绕其轴转动,空气的阻力矩与角速 度成正比,比例系数C 为一常量.若转动部分对其轴的转动惯量为J,问:(1) 经过多少时 间后其转动角速度减少为初角速度的一半?(2) 在此时间内共转过多少转? 分析 由于空气的阻力矩与角速度成正比,由转动定律可知,在变力矩作用下,通风机叶片 的转动是变角加速转动,因此,在讨论转动的运动学关系时,必须从角加速度和角速度的定 义出发,通过积分的方法去解. 解 (1) 通风机叶片所受的阻力矩为M =-Cω,由转动定律M =Jα,可得叶片的角加速度 为

()J根据初始条件对式(1)积分,有%-1-5a由于C 和J均为常量,得=W,e-arlJ(2) 当角速度由00→1200时,转动所需的时间为1==n2(2)根据初始条件对式(2)积分,有'do=lae-adt0-2即在时间内所转过的圈数为_ JooN=21-4nc4一21在光滑的水平面上有一木杆,其质量m1=1.0kg,长1=40cm,可绕通过其中点并与之垂直的轴转动.一质量为m2=10g的子弹,以v=2.0X102㎡=s-的速度射入杆端,其方向与杆及轴正交.若子弹陷入杆中,试求所得到的角速度,2题4-21图分析子弹与杆相互作用的瞬间,可将子弹视为绕轴的转动.这样,子弹射入杆前的角速度可表示为の,子弹陷入杆后,它们将一起以角速度の’转动.若将子弹和杆视为系统,因系统不受外力矩作用,故系统的角动量守恒.由角动量守恒定律可解得杆的角速度.解根据角动量守恒定理J.=(,+J.)a式中J,=m,(1/2)为子弹绕轴的转动惯量,J2为子弹在陷入杆前的角动量,=20/l为子弹在此刻绕轴的角速度.J,=m72/12为杆绕轴的转动惯量.可得杆的角速度为
J Cω t ω α = = − d d (1) 根据初始条件对式(1)积分,有 t J C ω ω ω t ω d d 0 0 = − 由于C 和J 均为常量,得 Ct J ω ω e / 0 − = (2) 当角速度由ω0 → 12 ω0 时,转动所需的时间为 ln 2 C J t = (2) 根据初始条件对式(2)积分,有 θ ω e t Ct J θ t d d / 0 0 0 − = 即 C Jω θ 2 0 = 在时间t 内所转过的圈数为 C θ Jω N 2π 4π 0 = = 4 -21 在光滑的水平面上有一木杆,其质量m1 =1.0 kg,长l =40cm,可绕通过其中点 并与之垂直的轴转动.一质量为m2 =10g 的子弹,以v =2.0×10 2 m· s -1 的速度射入杆端, 其方向与杆及轴正交.若子弹陷入杆中,试求所得到的角速度. 分析 子弹与杆相互作用的瞬间,可将子弹视为绕轴的转动.这样,子弹射入杆前的角速度 可表示为ω,子弹陷入杆后,它们将一起以角速度ω′ 转动.若将子弹和杆视为系统,因系统 不受外力矩作用,故系统的角动量守恒.由角动量守恒定律可解得杆的角速度. 解 根据角动量守恒定理 J ω = (J + J )ω 2 1 2 式中 ( ) 2 J 2 = m2 l / 2 为子弹绕轴的转动惯量,J2ω为子弹在陷入杆前的角动量,ω=2v/l 为子 弹在此刻绕轴的角速度. /12 2 1 1 J = m l 为杆绕轴的转动惯量.可得杆的角速度为