
④ 求N(A) ∴.N(A=B(A)+jC(A) 2sm+-(导学汀 =X2 PN=0 由此题可见,求非线性环节的描述函数只要这固定四步。 同学们可以研究一下,具有什么特点的非线性环节C的结果 是0,什么时候不为0,当C=0时,pw=0且 B=x,=N(A) 下面我们通过例2来说明一类复杂的非线性环节描述函数 的求法。所谓复杂非线性环节,通常是指含有两个或以上非 线性环节
线性环节。 的求法。所谓复杂非线性环节,通常是指含有两个或以上非 下面我们通过例 来说明一类复杂的非线性环节描述函数 是 ,什么时候不为 ,当 时, 且 同学们可以研究一下,具有什么特点的非线性环节 的结果 由此题可见,求非线性环节的描述函数只要这固定四步。 求 2 ( ) 0 0 0 0 0 [sin 1 ( ) ] 2 ( ) ( ) ( ) ( ) 2 1 2 1 2 1 1 B x N A C C x A A A k N A B A j C A N A N N = = = = = = = + − = + − ④

例2求 M -M y=x 描述函数。 解:① 设x(t)=Asin wt,.设法求出y(t)的分段表示的数学模型 M+Asin wt 显然:x0=-M+Asin wi 0<wt<π π<wt<2π y0- (M+Asin wt)3 0<wt<元 (-M+Asin wt)3 π<wt<2π 注意:表示成wt的变换范围段,是因为要对wt作积分
注意:表示成 的变换范围段,是因为要对 作积分 显然: 设 设法求出 的分段表示的数学模型 w t w t M A w t w t M A w t w t y t M A w t w t M A w t w t x t x t A w t y t − + + = − + + = = ( sin ) 2 ( sin ) 0 ( ) sin 2 sin 0 ( ) ( ) sin , ( ) 3 3 2 2 例2 求 描述函数。 解:①

解:② 计算B、C B号贰snidow) [3w4++] C-忌子为asm =0 ③ 求N(A: N(A=4 A 4M3M+4+ A π
0 ( ) cos ( ) 2 8 8 6 3 4 ( )sin ( ) 2 0 2 2 2 3 3 0 2 = = = + + + = y t wtd wt A C A A A M M A M y t wtd wt A B 解:② 计算B、C ③ 2 2 3 8 8 6 3 4 ( ) ( ): A A M M A M N A N A = + + + 求
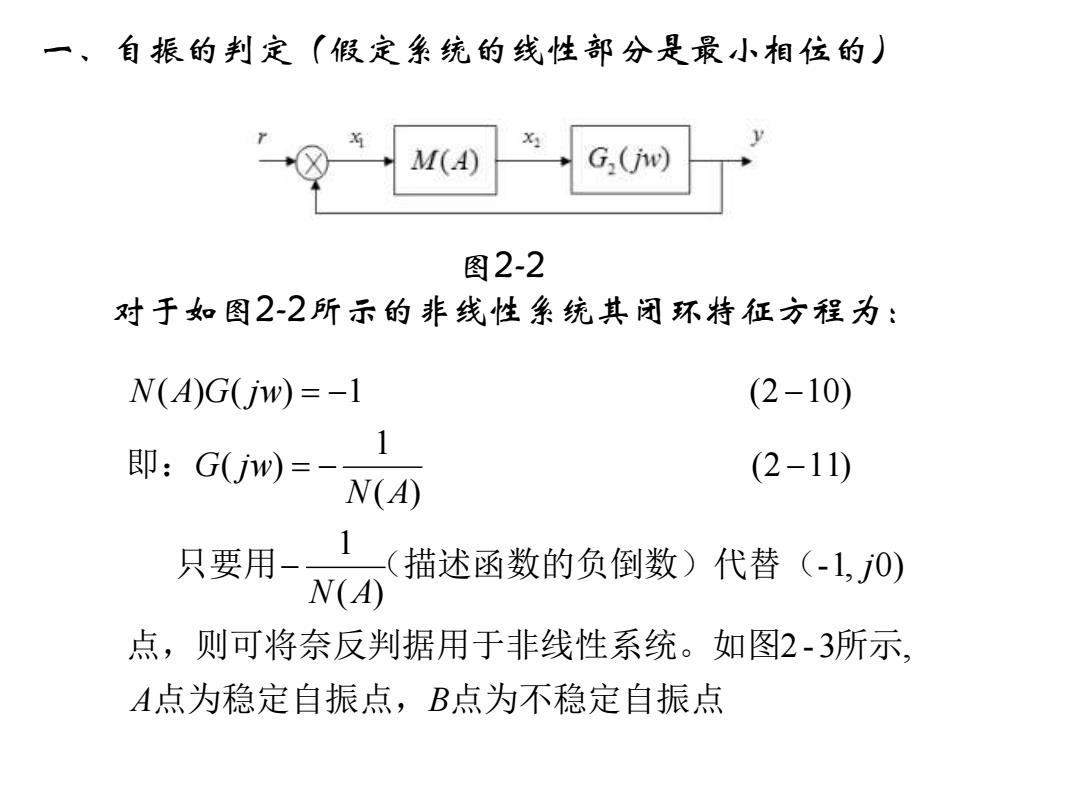
一、自振的判定(假定系统的线性部分是最小相位的) X: M(A) G,(jw) 图2-2 对于如图2-2所示的非线性条统其闭环特征方程为: N(A)G(jw)=-1 (2-10) 即:G(jw)=- N(A) (2-11) 只要用- 描述函数的负倒数)代替(-1,0) N(A) 点,则可将奈反判据用于非线性系统。如图2-3所示 A点为稳定自振点,B点为不稳定自振点
一、自振的判定(假定系统的线性部分是最小相位的) 图2-2 对于如图2-2所示的非线性系统其闭环特征方程为: 点为稳定自振点, 点为不稳定自振点 点,则可将奈反判据用于非线性系统。如图 所示 只要用 (描述函数的负倒数)代替( 即: A B j N A N A G j w N A G j w 2 -3 , -1, 0) ( ) 1 (2 11) ( ) 1 ( ) ( ) ( ) 1 (2 10) − = − − = − −
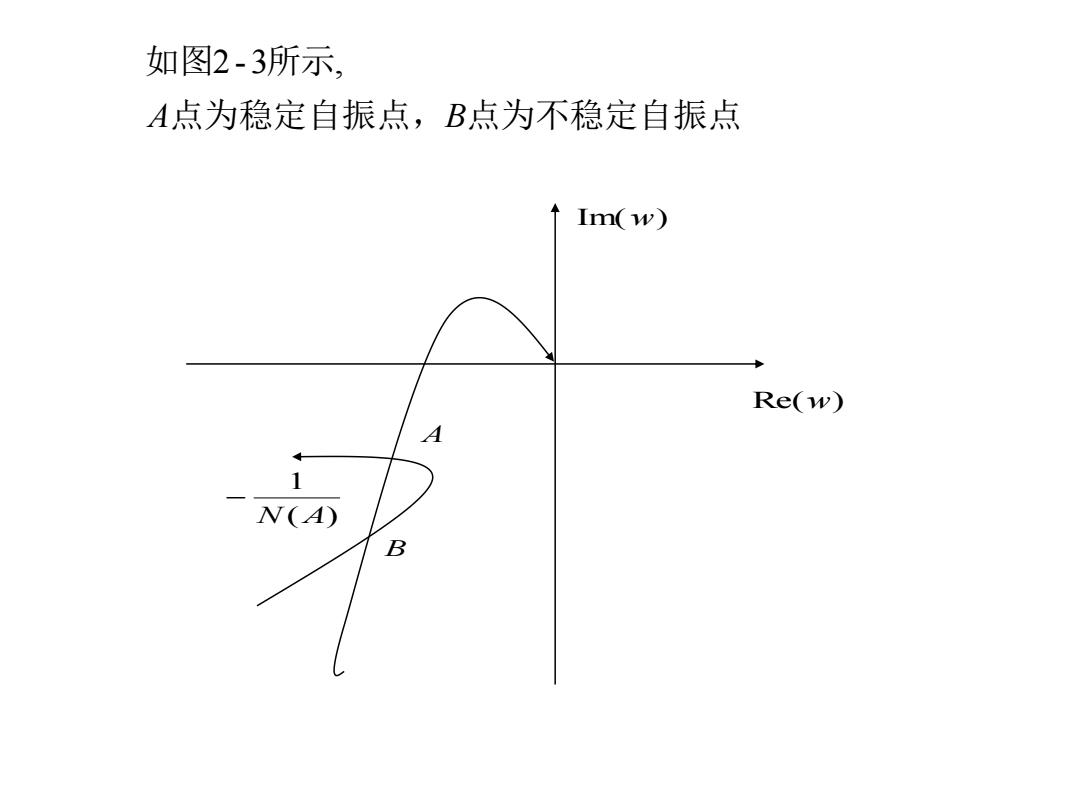
如图2-3所示 A点为稳定自振点,B点为不稳定自振点 ↑Im(w) Re(w) A -N(A) B
点为稳定自振点, 点为不稳定自振点 如图 所示 A B 2 -3 , Im(w) Re(w) A B ( ) 1 N A −