
二、怎样确定自振点的A和W? 例1: K s(s+1)0.2s+1) (1)判定K取何值时系统会有自振? (2)当k=10时,求自振的A和W. 解: 0我0子m 求1 和G(jw)的极坐标图 N(A) 并画出、1 N(A) -1 π A≥1 N(4) 2 h-1 "AA\ -42
二、怎样确定自振点的A和W? 例1: (1) 判定K取何值时系统会有自振? (2) 当k=10时,求自振的A和W. 解: (1) ⅰ = + − − 2 1 1 1 1 1 sin 2 ( ) ( ) A A A N A N A 求 1 1 1 1 1 sin 1 2 - ( ) -1 ( ) ( ) -1 ( ) -1 2 1 + − = − A A A A N A G j w N A N A 求 并画出 和 的极坐标图 s(s +1)(0.2s +1) 1 K 1 -1 -1 —
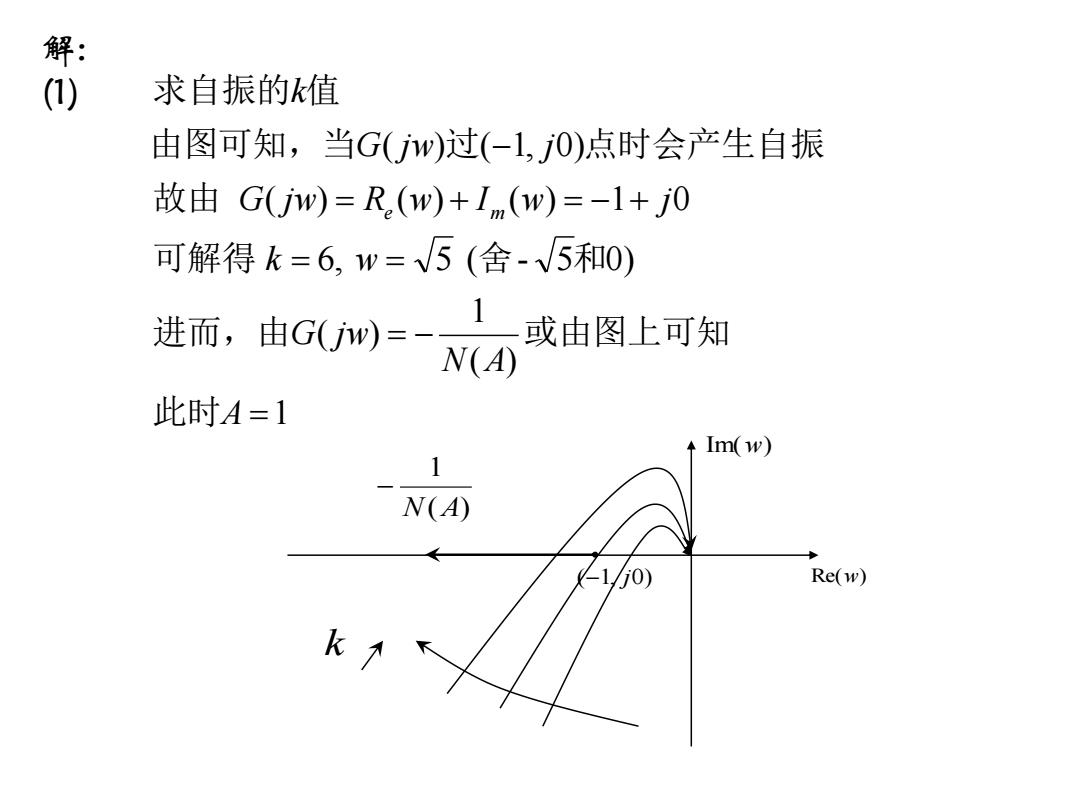
解: (1) 求自振的k值 由图可知,当G(w)过(-1,0)点时会产生自振 故由G(jw)=R(w)+Im(w)=-1+j0 可解得k=6,w=V5(舍-√5和0) 进而,出Gm)=- 1- 或由图上可知 N(A) 此时A=1 Im(w) N(A) -10) Re(w) k
解 : (1) ⅲ 1 ( ) 1 ( ) 6, 5 ( - 5 0) ( ) ( ) ( ) 1 0 ( ) ( 1, 0) = = − = = = + = − + − A N A G j w k w G j w R w I w j G j w j k e m 此时 进而,由 或由图上可知 可解得 舍 和 故由 由图可知,当 过 点时会产生自振 求自振的 值k ( ) 1 N A − (− 1 , j 0 ) Im( w ) Re( w )

解: 10 (2)当k=10时,由G(jw)= jw(jw+1)(0.2jw+1) 1 N(A) 可解得:w=√5(舍-√5和0)A=23 对于非线性系统的线性部分是最小的相位系统,判定稳定性 的方法是看G(w)和-、1 的极坐标曲线是否相交、交点是 N(A) 否稳定。并用上例方法求出A和w。这里需要特别说明的是相 平面分析方法是一种近似分析方法
解 : (2) 平面分析方法是一种近似分析方法。 否稳定。并用上例方法求出 和 。这里需要特别说明的是相 的方法是看 和 的极坐标曲线是否相交、交点是 对于非线性系统的线性部分是最小的相位系统,判定稳定性 可解得: 舍 和 、 当 时,由 A w N A G j ww A N A j w j w j w k G j w( ) 1 ( ) 5 ( - 5 0) 2 3 ( ) 1 ( 1)(0.2 1) 10 10 ( ) − = = = − + + = =

3相平面分析法 相平面分析方法仅适用于低维空间(1、2、3维空间),条件为: (①)只能分析一、二阶系统(线性部分)。(2)系统响应的高阶分量 不可忽略。即线性系统部分的低通滤波性不够好。(3)系统输入 r(t)≠0或非sin wti函数。 3.1相平面的绘制及其概念 3.2二阶线性系统的相平面图及其特性 3.3奇点、与极限环 3.4线性控制系统分析实例 3.5由相轨迹求时域解的问题
3 相平面分析法 3.1 相平面的绘制及其概念 3.2 二阶线性系统的相平面图及其特性 3.3 奇点与极限环 3.4 线性控制系统分析实例 3.5 由相轨迹求时域解的问题 或非 函数。 不可忽略。即线性系统部分的低通滤波性不够好。 系统输入 只能分析一、二阶系统 线性部分 。 系统响应的高阶分量 相平面分析方法仅适用于低维空间 、、维空间 条件为: r(t) 0 sin wt (3) (1) ( ) (2) (1 2 3 ),

3.1相平面的绘制及其概念 设某二阶非线性系统方程为: x。+a1(xxe)x。+a(xxe)x。=0 (3-1) 令:x=x,y=元。则: x=y (3-2) y=-a(xy)y-ao(xy)x 如果以X为横轴,以y为纵轴建立一个平面—状态平 面(相平面),平面上的某一点(X,y)均为时间函数,它 们在相平面上随时间变化形成的轨迹称之为相轨迹。其绘 制方法有两种: y 相平面 (0,0) X
3.1 相平面的绘制及其概念 (3 2) ( ) ( ) ( ) ( ) 0 (3 1) 1 0 1 0 − = − − = = = + + = − y a x y y a x y x x y x x y x x a x x x a x x x c c c c c c c c c 令: , 则: 设某二阶非线性系统方程为: 如果以x为横轴,以y为纵轴建立一个平面——状态平 面(相平面),平面上的某一点(x,y)均为时间函数,它 们在相平面上随时间变化形成的轨迹称之为相轨迹。其绘 制方法有两种: x y 相平面 (0,0)