
描述函数分析的前提条件是: (I)r(t)=0,x=Asin wt即描述函数是研究简谐自振荡的近似方法。 (2)非线性元件不是时间函数,且关于原点对称。 (3)G(0w)是具有好的低通滤波性。 当x,=Asin wt,则x2=f(Asin wt).将x,展成傅里叶级数: 2x+(B.sin kwt+cg cos kwt) (2-1) k=0 则:x=广x(t)t=0(关于原点对称) (2-2) &-子s0smw (2-3) C-2s0 )eoskd网y 7
描述函数分析的前提条件是: (1) 即描述函数是研究简谐自振荡的近似方法。 (2) 非线性元件不是时间函数,且关于原点对称。 (3) G(jw)是具有好的低通滤波性。 r(t) 0, x Asin wt = 1 = (2 3) ( ) cos ( ) 2 ( )sin ( ) 2 : ( ) 0 ( ) (2 2) ( sin cos ) (2 1) sin , ( sin ). 0 2 0 2 0 2 0 2 0 1 2 2 − = = = = − = + + − = = − = C x t kwtd wt B x t kwtd wt x x t dt x x B kwt c kwt x A wt x f A wt x k k n k k k 则 关于原点对称 当 则 将 展成傅里叶级数:

.G(w)具有低通率波性」 .x2≈B1 sin wt+C cos wt (2-4) 即:x2(t)=x2sin(wt+pv) (2-5) 其中:x=VB+Cw=g B 在此意义上,可用频率特性方法表示N(A)特性,即: M0=是40-号+月=风0+00 (2-6) 至此,可归纳出关于原点对称的奇函数的非线性元件 描述函数的求法: 描述函数:N(A)=B(A)+jC(A) (2-7) 其中:小新x0sn (2-8) c0-子s0 cw0 2
= − = − = + − = = + = + − = + = = + − + − − 0 2 0 2 2 1 1 1 2 1 1 1 2 2 1 2 2 2 1 1 ( ) cos ( ) (2 9) 2 ( ) ( )sin ( ) (2 8) 2 ( ) ( ) ( ) ( ) (2 7) , ( ) ( ) ( ) (2 6) , ( ) , : : ( ) sin( ) (2 5) sin cos (2 4) ( ) , x t wtd w t A C A x t wtd w t A B A N A B A j C A B A j C A A C j A B A x N A N A B C x B C t g x t x w t x B w t C w t G j w N N N 其中: 描述函数: 描述函数的求法: 至此 可归纳出关于原点对称的奇函数的非线性元件 在此意义上 可用频率特性方法表示 特性 即: 其中 即 具有低通率波性

二、典型非线性元件的描述函数 例1:试求饱和特性 X2 a X 的描述函数。 解:①设x(t)=Asin wt 用图解法求出该非线性环节输出量的波形
二、典型非线性元件的描述函数 例1:试求饱和特性 的描述函数。 解:①设 用图解法求出该非线性环节输出量 的波形 x (t) Asin wt 1 = 2 x
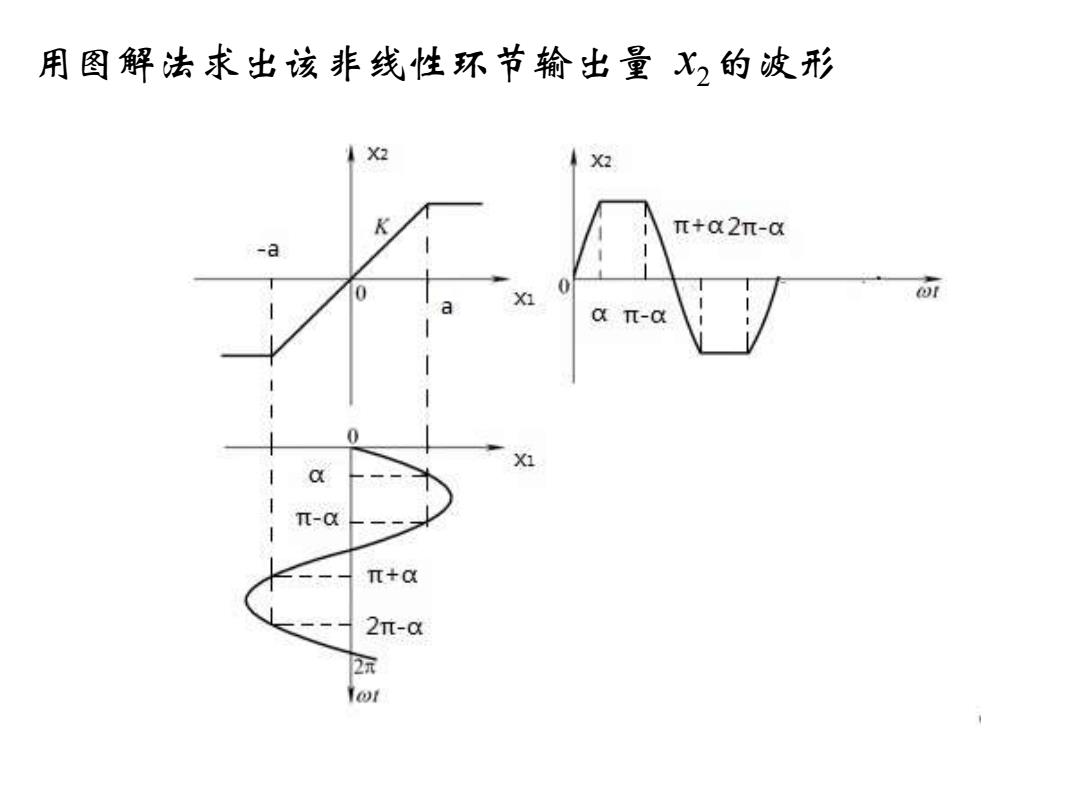
用图解法求出该非线性环节输出量X,的波形 X2 X2 π+C2π-c -a a Tt-d X1 π- π+C 2m-0 2元 Tor
用图解法求出该非线性环节输出量 x2 的波形

②写出周期函数x,()的分段解析表达式, 共中a=m月 kAsin wt 0≤wt≤0 ka C<wt≤π- x2(t)=kAsin wt π-C,wt≤π+C -ka π+C<wt≤2π-C kAsin wt 2π-0≤wt≤2π ③) 按公式计算B、C(x,和pw) 月=0 )an0-m号+-(身1 C()c0 wtw)0
②写出周期函数 的分段解析表达式, 其中 − − + − − + − = sin 2 2 2 sin , sin 0 ( ) 2 k A wt wt k a wt k A wt wt k a wt k A wt wt x t ( ) 2 x t A 1 a sin − = ( ) cos ( ) 0 2 [sin 1 ( ) ] 2 ( )sin ( ) 2 ( ) 0 1 2 1 2 0 1 2 1 1 2 = = = = + − − x t wtd wt A C A a A a A k a x t wtd wt A B B C x ③ 按公式计算 、 和 N