受扭杆件内力计算的例题 例3: 如图杆件,已知转速n=100r/min,输入功率P4=40kW, 输出功率PB=Pc=20kW,试绘制扭矩图。 解: 1.计算外力偶: M4=9549B=3820N.m Mn=Mc=9549B=1910N.m 第三章扭转 11
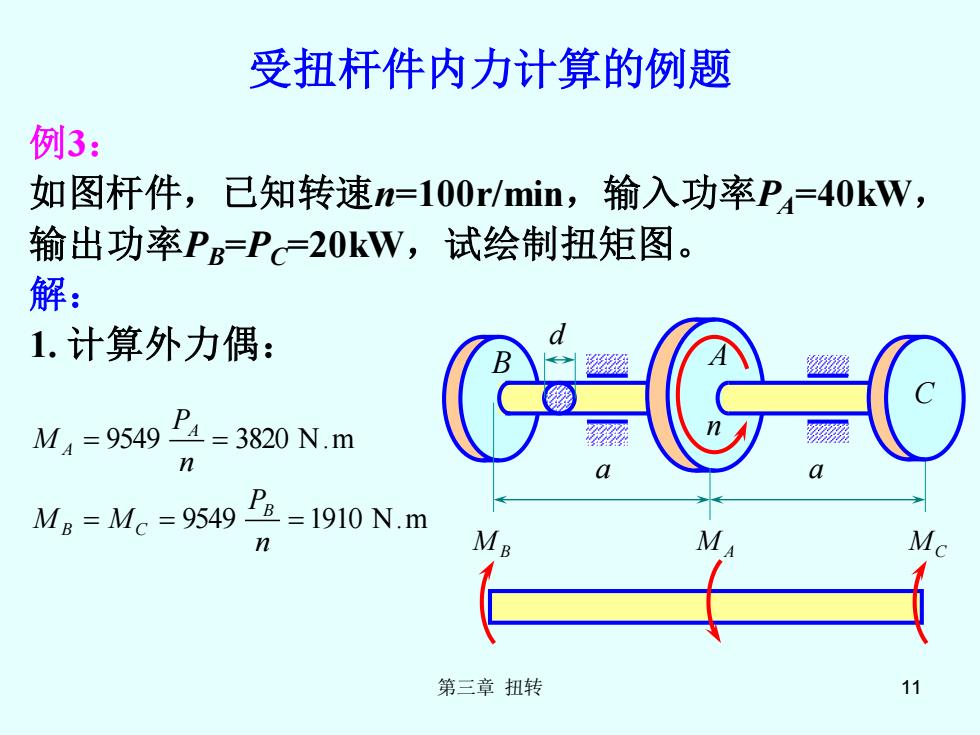
第三章 扭转 11 受扭杆件内力计算的例题 例3: 如图杆件,已知转速n=100r/min,输入功率PA=40kW, 输出功率PB=PC=20kW,试绘制扭矩图。 解: 1. 计算外力偶: 9549 1910 N.m 9549 3820 N.m = = = = = n P M M n P M B B C A A B A a a C n d M B M A MC
受扭杆件内力计算的例题 例3:(续) 2.绘制扭矩图: TEA-MB:TAC-MC MB 分析: 该杆件上的载荷力系关于杆件中截面A对称。可以发现, T的分布关于杆件中截面A是反对称的。而且在中截面A 上,T4=0。 第三章扭转 12
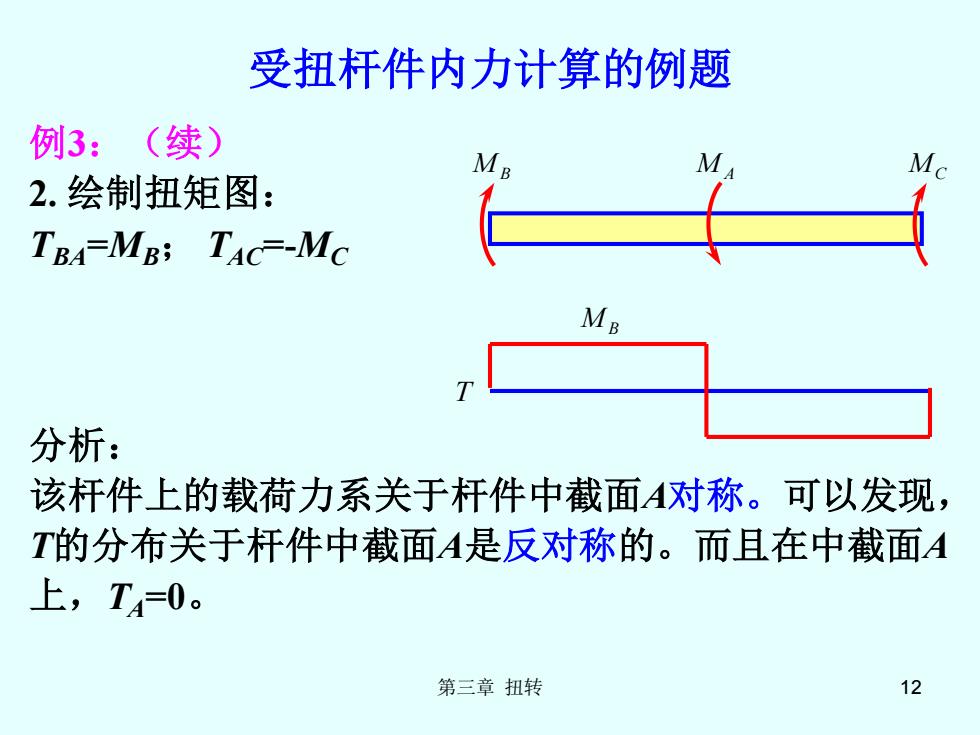
第三章 扭转 12 受扭杆件内力计算的例题 例3:(续) 2. 绘制扭矩图: TBA=MB; TAC=-MC 分析: 该杆件上的载荷力系关于杆件中截面A对称。可以发现, T的分布关于杆件中截面A是反对称的。而且在中截面A 上,TA=0。 M B T M B M A MC

第四节等直圆轴扭转的应力强度条件 1.横截面上的应力分布 在分析圆截面杆件受扭转的应力分布时,可以通 过如下方法: 变形几何关系 找到切应变在横截面上的分布规律 剪切胡克定律 建立切应力分布与扭转变形的关系 内力场合成内力主矢、主矩 切应力是扭矩在横截面上分布场的集度,由此确 定扭转变形的表达式,并最终确定切应力在横截面上 的分布公式
第四节 等直圆轴扭转的应力 强度条件 1. 横截面上的应力分布 在分析圆截面杆件受扭转的应力分布时,可以通 过如下方法: 变形几何关系 找到切应变在横截面上的分布规律 剪切胡克定律 建立切应力分布与扭转变形的关系 内力场合成内力主矢、主矩 切应力是扭矩在横截面上分布场的集度,由此确 定扭转变形的表达式,并最终确定切应力在横截面上 的分布公式

1.1变形几何关系 通过实验知,圆截面杆发生扭转变形后:横截面仍 为平面,仍垂直于轴线,绕圆心刚体旋转;横截面绕圆 心的角位移为扭转角;半径仍为直线段且长度不变。 这一规律称为圆截面杆扭转变形的平面假设。 第三章扭转 14
第三章 扭转 14 1.1 变形几何关系 通过实验知,圆截面杆发生扭转变形后:横截面仍 为平面,仍垂直于轴线,绕圆心刚体旋转;横截面绕圆 心的角位移为扭转角;半径仍为直线段且长度不变。 这一规律称为圆截面杆扭转变形的平面假设。 R a x b c d d O O1 d x O O1 c' d ' d M e M e d x
1.2切应变分布 根据平面假设进行几何分析,得 do Yo=p dx dx R a +do a dx a do 第三章扭转 15
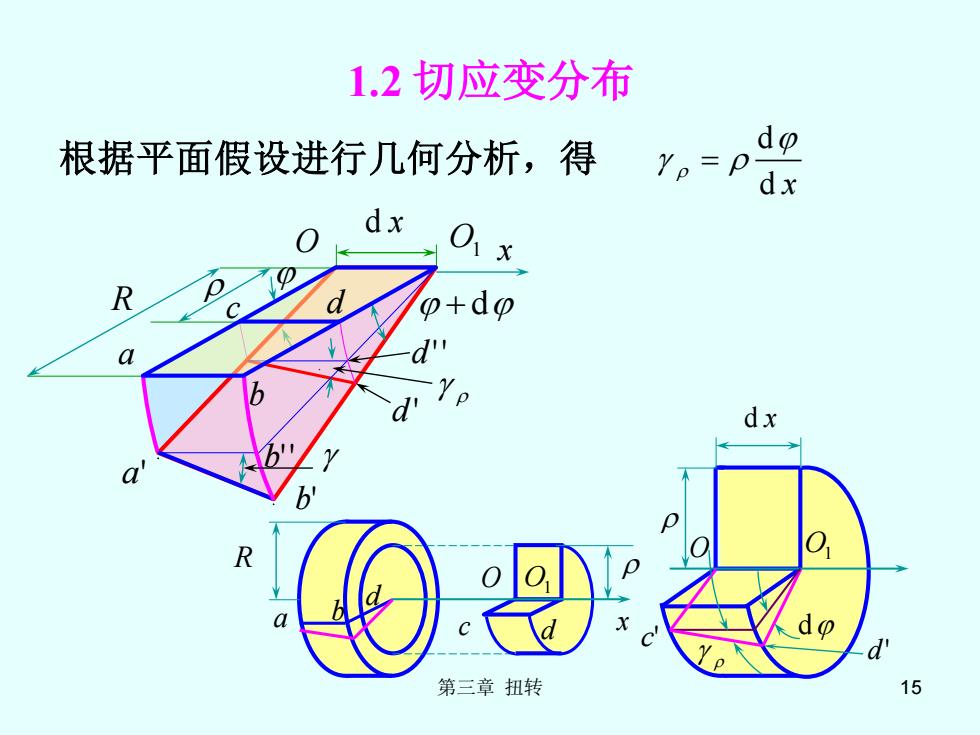
第三章 扭转 15 1.2 切应变分布 根据平面假设进行几何分析,得 d x d = R a x b c d d O O1 d x O O1 c' d ' d O O1 d x R a a' b d ' d ' ' b' b'' + d x c d