《力学》课程教学资源（PPT课件）材料力学——扭转

1.3切应力分布 应用物理关系： t。=Gp do dx 1.4静力学关系 极惯性矩 T-,pd4=G2,pd1-c8, dx 1,=∫p2dA dp p d/2 do T 扭转变形率dxGl。 G1,称为圆截面杆的扭转刚度 扭转切应力： 第三章扭转 16

第三章 扭转 16 1.3 切应力分布 应用物理关系： 1.4 静力学关系 极惯性矩 扭转变形率 GIp称为圆截面杆的扭转刚度 扭转切应力 x G d d   =  p 2 p p 2 d d d d d d d d d GI T x I A I x A G x T A G A A A = = = = =            d   d / 2 O   d A    p I T =

1.5最大切应力 最大切应力：tmx= T Pmax max 抗扭系数： W。= Pmax 、d4 实心圆截面：， 32 W。 16 -a），-a) D4 圆管截面： 1=32 G。sG 圆截面杆的扭转刚度：GIp 32 G1。sG 32 -a） 第三章扭转 17

第三章 扭转 17 1.5 最大切应力 最大切应力： 抗扭系数： 实心圆截面： 圆管截面： 圆截面杆的扭转刚度：GIp ( ) ( ) 4 3 p 4 4 p 3 p 4 p max p p max p max 1 16 1 32 32 16          = − = − = = = = D W D I d W d I I W I T ( ) 4 4 p 4 p 1 32 32    = − = D GI G d GI G T T   max 

2.斜截面应力 2.1纯剪切 纯扭轴的平面微单元体上无正应力，仅有切应力， 这种应力状态称纯剪切。 2.2切应力互等定理 在两个相互垂直的截面或表面上，与两平面交线 相垂直的切应力分量数值相等，且同时指向或背离交 线。可以证明，该定理适用于各种其它的应力状态。 T=t 第三章扭转 18

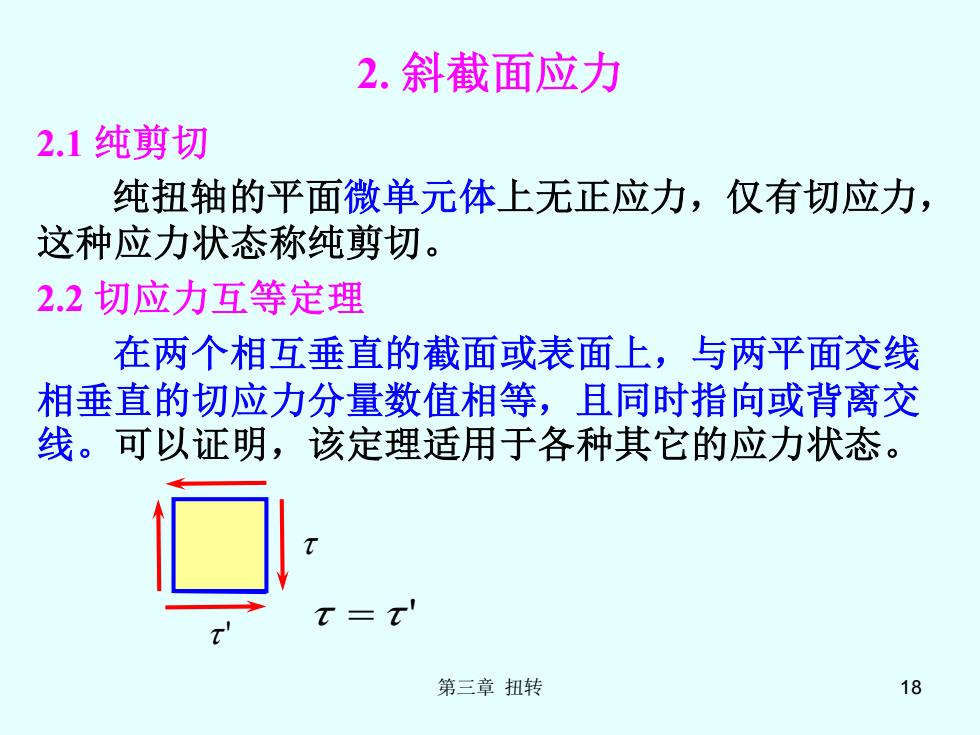
第三章 扭转 18 2. 斜截面应力 2.1 纯剪切 纯扭轴的平面微单元体上无正应力，仅有切应力， 这种应力状态称纯剪切。 2.2 切应力互等定理 在两个相互垂直的截面或表面上，与两平面交线 相垂直的切应力分量数值相等，且同时指向或背离交 线。可以证明，该定理适用于各种其它的应力状态。  = '  ' 