
材料力学习题 第一章绪论 P10,1-4 己知:=100mm,△/=5x102mm 求:平均应变 解: E-45x10-mm P14,1-5 已知:g=0.03mm 求:ey,7B。 求:OB平均应变:B点ABC角度改变 解: 1-5 a=00=25x10- -2g(8)-25x0 P14,1-6 己知:圆形薄板,R=80.00mm,△R=3×103mm。求:£响,Y向e 求:径向平均应变:周向平均应变: 解: E径前=△R/R=3.75×10- 5w贤 2πR
材料力学习题 第一章 绪论 P10,1-4 已知:l=100mm,Δl =5×10-2mm。 求:平均应变 解: mm l l 4 5 10− = = P14,1-5 已知:vB=0.03mm 求:εby,γB。 求:OB 平均应变;B 点 ABC 角度改变 解: 1-5 1-6 1 4 4 2.5 10 ' 2 2 2.5 10 − − − = = − = = OB OA tg OB v B B yB P14,1-6 已知:圆形薄板,R=80.00mm,ΔR=3×10-3mm。求:ε 径向,γ 周向。 求:径向平均应变;周向平均应变; 解: 周向 径向 径向 = = + − = = = − R R R R R R R R 2 2 ( ) 2 / 3.75 10 5
材料力学习题 第二章拉压与剪切 孙训芳 22F1 F22F125 P44,2-1 绘轴力图。 2 F 解: F F 如图。 F 2 2 a F d P44,2-2 3 绘轴力图。A0.0004m2,求各截面应力。 3 -F-50 MPa 10kN 如国,学=-5m P45,2-3 ,320kN210kN120kN 绘轴力图。A1=0.0002m2,A-0.0003m2,A:=0.0004m2,求各截 应力。 13 解 10kN -10 MPa 如图。oea-52=-383M Co -F-=2 MPa P45,2-6 F=10kN,4=0.0001m2,=0°,30°, 45°,60°,90°,求各斜截面应力 如图。 Xw
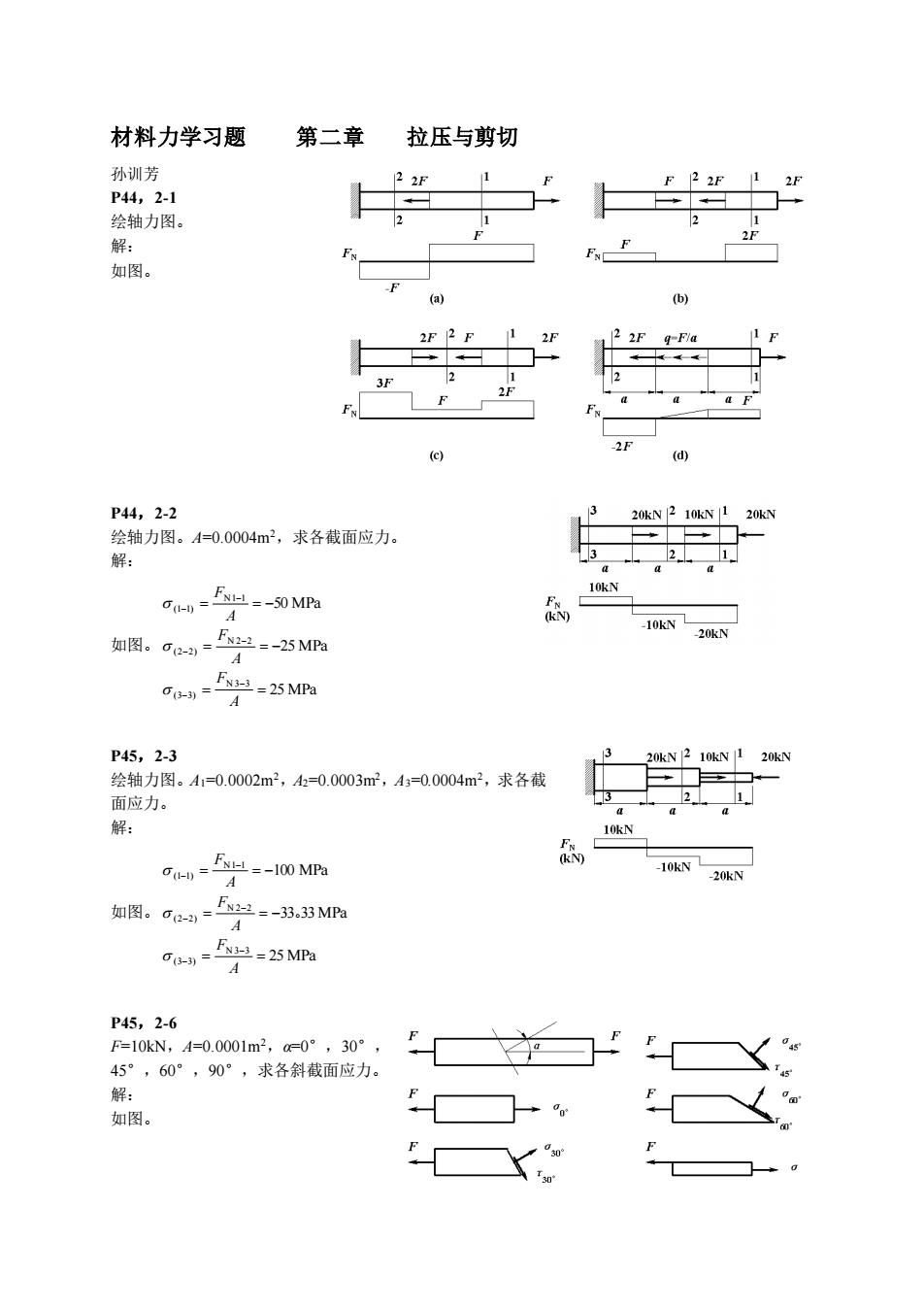
材料力学习题 第二章 拉压与剪切 孙训芳 P44,2-1 绘轴力图。 解: 如图。 P44,2-2 绘轴力图。A=0.0004m2,求各截面应力。 解: 如图。 25 MPa 25 MPa 50 MPa N 3 3 (3 3) N 2 2 (2 2) N1 1 (1 1) = = = = − = = − − − − − − − A F A F A F P45,2-3 绘轴力图。A1=0.0002m2,A2=0.0003m2,A3=0.0004m2,求各截 面应力。 解: 如图。 25 MPa 33 33 MPa 100 MPa N 3 3 (3 3) N 2 2 (2 2) N1 1 (1 1) = = = = − = = − − − − − − − A F A F A F 。 P45,2-6 F=10kN,A=0.0001m2,α=0°,30°, 45°,60°,90°,求各斜截面应力。 解: 如图
=-=100 MPa=0 =c cos30*=75 MPa =o sin=43.30 MPa 6g=6cos245°=50MPTg=6sim45°cos45=50MPa a=G cos60*=25 MPa =a sin 60*cos60*=43.30 MPa 0w=6c0s290°=0tw=6sn90°c0s90°=0 P45,2-8 b0.2m,E=10GPa,作轴力图,求各段应力、应变,总变形。 解: 1轴力如图。 2各段应力、应变 a2MP an6MPs c=g=-25x106c=可=-65x10- 3总变形 M=Wc+c=-3.75x10-9.75x10=-135×103m P46,2-11 已知a,F,E,4。求CD的距离改变△cD 解: 1横向应变 e台 2CD的距离改变△cD Ac-CD=-1. P46,2-12 己知:AB刚性,杆1、2、3材质相同E=210GPa =1m =4=00001m2 As=0.00015m F=20kN。试求C的水平、铅垂位移 解: 1内力 2变形 2 2 EA 2EA =4.7×10m2= =4.762×10m3=0 EA,2EA 3位移
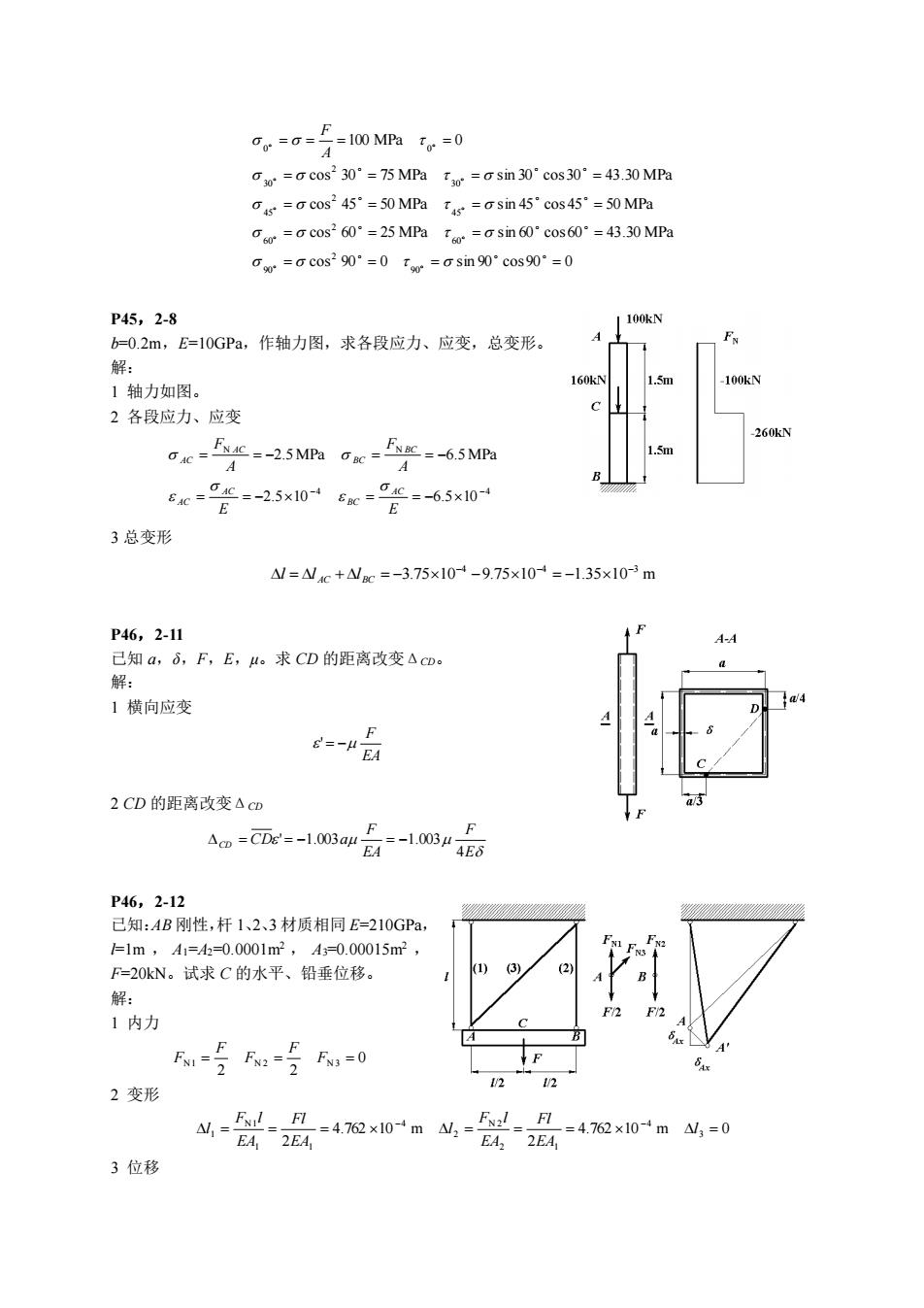
cos 90 0 sin 90 cos90 0 cos 60 25 MPa sin 60 cos 60 43.30 MPa cos 45 50 MPa sin 45 cos 45 50 MPa cos 30 75 MPa sin 30 cos30 43.30 MPa 100 MPa 0 90 2 90 60 2 60 45 2 45 30 2 30 0 0 = = = = = = = = = = = = = = = = = = = = A F P45,2-8 b=0.2m,E=10GPa,作轴力图,求各段应力、应变,总变形。 解: 1 轴力如图。 2 各段应力、应变 4 4 N N 2.5 10 6.5 10 2.5 MPa 6.5MPa − − = = − = = − = = − = = − E E A F A F AC BC AC AC BC BC AC AC 3 总变形 3.75 10 9.75 10 1.35 10 m −4 −4 −3 l = l AC +lBC = − − = − P46,2-11 已知 a,δ,F,E,μ。求 CD 的距离改变ΔCD。 解: 1 横向应变 EA F ' = − 2 CD 的距离改变ΔCD E F EA F CD CD a 4 = ' = −1.003 = −1.003 P46,2-12 已知:AB 刚性,杆 1、2、3 材质相同 E=210GPa, l=1m , A1=A2=0.0001m2 , A3=0.00015m2 , F=20kN。试求 C 的水平、铅垂位移。 解: 1 内力 0 2 2 N1 = N 2 = FN 3 = F F F F 2 变形 4.762 10 m 0 2 4.762 10 m 2 3 4 2 1 N 2 2 4 1 1 N1 1 = = = = = = = − − l EA Fl EA F l l EA Fl EA F l l 3 位移
A点位移 6=M,=4.762×10m-→)6=-d,=-4.762×10m) B点位移 6=-4M2=-4.762×10°m) C点位移 。=d=472x0-m)66-8-47a×10m山 2 P47,2-17 己知:两杆长度、截面和材质都相同。试求两杆应变能之比。 解 内力 Fu-F F:-fx 2应变能 2EA P48,2-21 己知:AB、AD两杆材质相同,[o小I7OMP 截面各为两根等边角钢。试选择型号。 307 解: 1内力 F-300 kNF0600 N 2m 2选择等边角钢型号 器销-10m AD杆选择No.80×6,AB杆选择No.100×10。 P49,2-25(1) 己知:AC、BD两杆材质相同,[d=17OMPa,E=210GPa:截面圆形, d=0.025m,=0.018m:F=100kN,并记其作用点为F点。试校核强度, 计算两杆变形,以及A、B两点的铅垂位移。 解 1内力 3m 人1-25=667w人:-号-33w 2校核强度
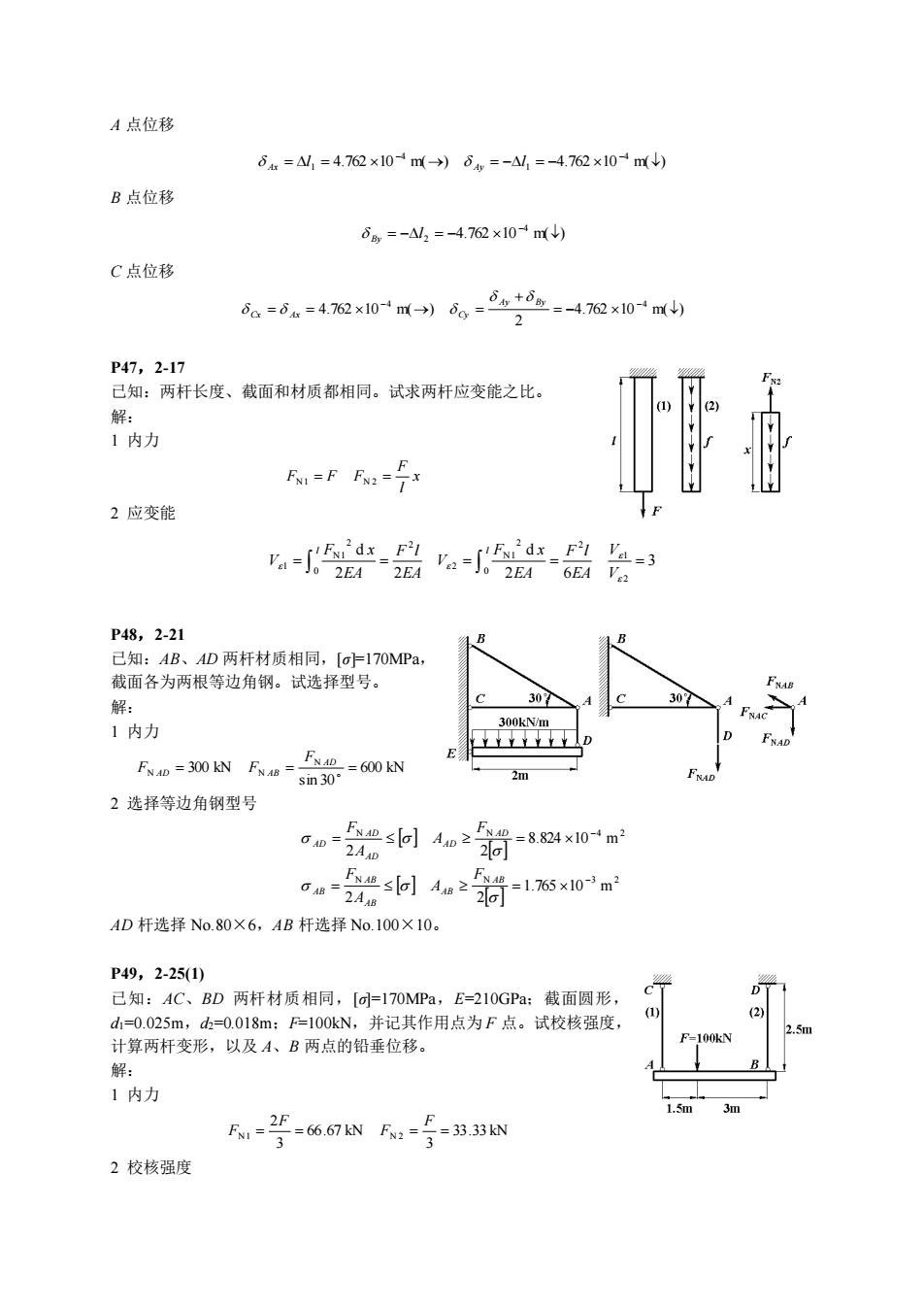
A 点位移 4.762 10 m( ) 4.762 10 m( ) 4 1 4 = 1 = → = − = − − − l l Ax Ay B 点位移 4.762 10 m( ) 4 = − 2 = − − l By C 点位移 4.762 10 m( ) 2 4.762 10 m( ) 4 4 = − + = = → = − Ay By − Cx Ax Cy P47,2-17 已知:两杆长度、截面和材质都相同。试求两杆应变能之比。 解: 1 内力 x l F FN1 = F FN 2 = 2 应变能 3 2 6 d 2 2 d 2 1 2 0 2 N1 2 2 0 2 N1 1 = = = = = V V EA F l EA F x V EA F l EA F x V l l P48,2-21 已知:AB、AD 两杆材质相同,[σ]=170MPa, 截面各为两根等边角钢。试选择型号。 解: 1 内力 600 kN sin 30 300 kN N N = N = = AD AD AB F F F 2 选择等边角钢型号 N N 3 2 N N 4 2 1.765 10 m 2 2 8.824 10 m 2 2 − − = = = = AB AB AB AB AB AD AD AD AD AD F A A F F A A F AD 杆选择 No.80×6,AB 杆选择 No.100×10。 P49,2-25(1) 已知:AC、BD 两杆材质相同,[σ]=170MPa,E=210GPa;截面圆形, d1=0.025m,d2=0.018m;F=100kN,并记其作用点为 F 点。试校核强度, 计算两杆变形,以及 A、B 两点的铅垂位移。 解: 1 内力 33.33 kN 3 66.67 kN 3 2 N1 = = N 2 = = F F F F 2 校核强度

。e-经=ssMsb]o经=H0Nm<间 满足强度要求。 3计算两杆变形 4、B两点的铅垂位移分别等于两杆变形。 P49,2-25(2) 将F作用于A,试计算F点的铅垂位移。 解: 1内力 ,=F=100kNF2=0 2计算两杆变形 3计算F点的铅垂位移 ,-2=167x10m P49,2-28 己知:如图薄壁管长度为b,材料弹性模量为E,内压为P,试计算管壁周向应 力,内半径的伸长。 解 1内力 Fx=rpb 2计算管壁周向应力 希-罗 3计算内半径的伸长 心6话
= = = = 131.0 MPa 4 135.8MPa 4 2 2 N 2 2 1 N1 d F d F AC BD 满足强度要求。 3 计算两杆变形 1.559 10 m 4 1.617 10 m 4 3 2 2 N 2 2 3 2 1 N1 1 − − = = = = E d F l l E d F l l A、B 两点的铅垂位移分别等于两杆变形。 P49,2-25(2) 将 F 作用于 A,试计算 F 点的铅垂位移。 解: 1 内力 FN1 = F =100 kN FN 2 = 0 2 计算两杆变形 2.425 10 m 0 4 2 3 2 1 N1 1 = = = − l E d F l l 3 计算 F 点的铅垂位移 1.617 10 m 3 2 1 −3 = = l Fy P49,2-28 已知:如图薄壁管长度为 b,材料弹性模量为 E,内压为 p,试计算管壁周向应 力,内半径的伸长。 解: 1 内力 FN = rpb 2 计算管壁周向应力 rp b rpb b F = = = N 3 计算内半径的伸长 E r p r r 2 = =