
第三章 扭转 第一节 概述 扭转是杆件的基本变形之一。 1.受力特点 杆件受绕轴线旋转的力偶或力偶系的作用,这些 力偶的旋转平面都垂直于杆件的轴线。 2.变形特点 横截面绕轴线旋转,两横截面间产生相对角位移, 称扭转角φ,纵向线段变形为螺旋线,与变形前的夹角 称为剪切角Y。 M Me 第三章扭转
第三章 扭转 1 第三章 扭转 第一节 概述 扭转是杆件的基本变形之一。 1. 受力特点 杆件受绕轴线旋转的力偶或力偶系的作用,这些 力偶的旋转平面都垂直于杆件的轴线。 2. 变形特点 横截面绕轴线旋转,两横截面间产生相对角位移, 称扭转角φ,纵向线段变形为螺旋线,与变形前的夹角 称为剪切角γ。 M e M e
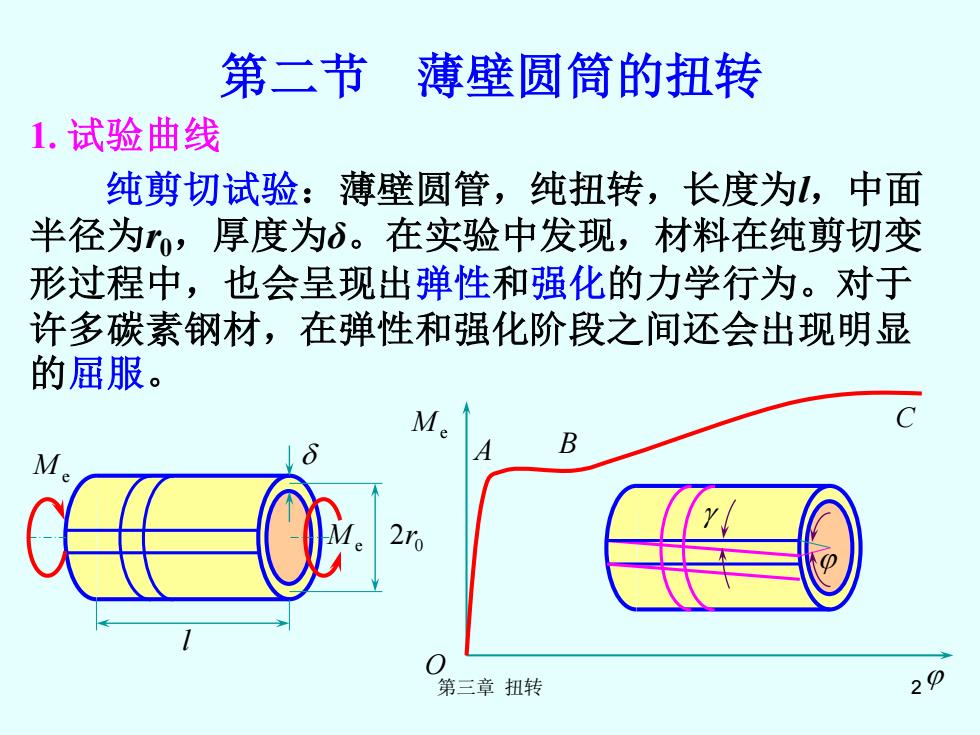
第二节薄壁圆简的扭转 1.试验曲线 纯剪切试验:薄壁圆管,纯扭转,长度为,中面 半径为,厚度为δ。在实验中发现,材料在纯剪切变 形过程中,也会呈现出弹性和强化的力学行为。对于 许多碳素钢材,在弹性和强化阶段之间还会出现明显 的屈服。 Me 第三章扭转
第三章 扭转 2 第二节 薄壁圆筒的扭转 1. 试验曲线 纯剪切试验:薄壁圆管,纯扭转,长度为l,中面 半径为r0,厚度为δ。在实验中发现,材料在纯剪切变 形过程中,也会呈现出弹性和强化的力学行为。对于 许多碳素钢材,在弹性和强化阶段之间还会出现明显 的屈服。 M e M e 2 0 r l O M e A B C

2.薄壁圆筒扭转切应力的简化计算 2ro 在纯剪切实验中,纵、横截面正 应力皆为零。 假设横截面切应力不沿厚度方向 变化。 由切应力乘以横截面积微元对圆 心的合矩等于外力偶,可得 7 Me=人nδds=∫。"oody M。=2m,26 Me 2m。26 第三章扭转 3
第三章 扭转 3 2. 薄壁圆筒扭转切应力的简化计算 在纯剪切实验中,纵、横截面正 应力皆为零。 假设横截面切应力不沿厚度方向 变化。 由切应力乘以横截面积微元对圆 心的合矩等于外力偶,可得 2 0 e 2 e 0 2 0 e 0 0 0 2 2 d d r M M r M r s r r S = = = = ' O 2 0 r T

3.切应变,剪切胡克定律 剪切角Y即为切应变,圆管两端的相对扭转角为φ, 小变形时切应变为 在纯剪切试验的弹性阶段中的线弹性段,φ正比例 于T,于是切应变正比例于切应力,即 -Gy 这个关系称剪切胡克定律。定律中的比例常数G称切 变模量,是材料的弹性系数。对于各向同性材料,E、 4、G三个弹性系数之间存在下式关系 E G= 21+4)) 第三章扭转 4
第三章 扭转 4 3. 切应变,剪切胡克定律 剪切角γ即为切应变,圆管两端的相对扭转角为φ, 小变形时切应变为 在纯剪切试验的弹性阶段中的线弹性段,φ正比例 于T,于是切应变正比例于切应力,即 这个关系称剪切胡克定律。定律中的比例常数G称切 变模量,是材料的弹性系数。对于各向同性材料,E、 μ、G三个弹性系数之间存在下式关系 = G l r0 = ( + ) = 2 1 E G
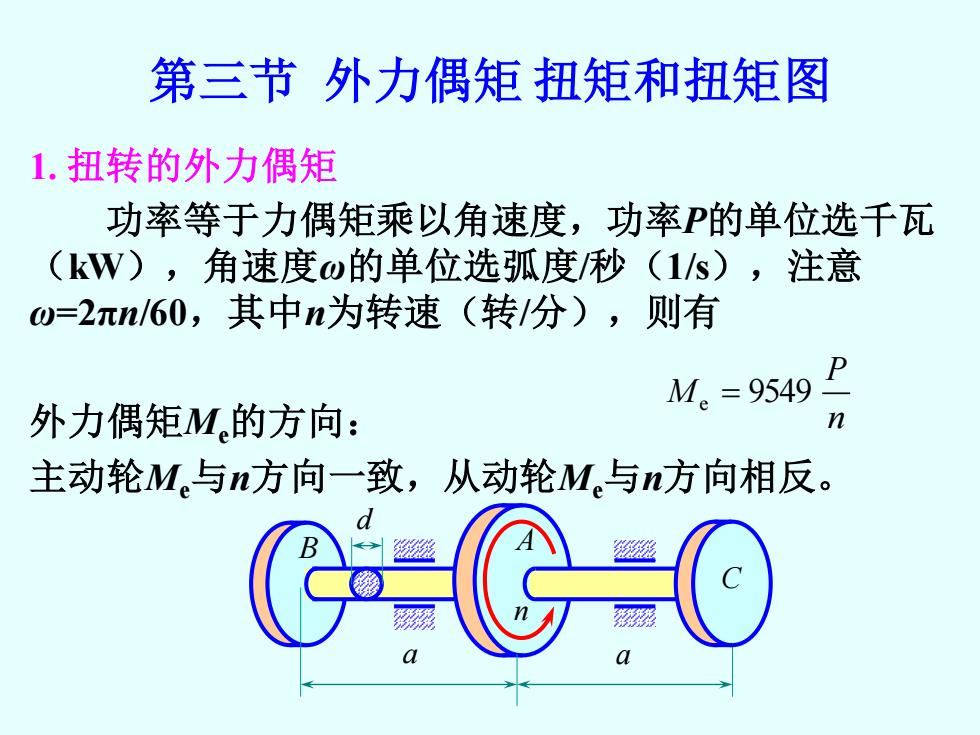
第三节外力偶矩扭矩和扭矩图 1.扭转的外力偶矩 功率等于力偶矩乘以角速度,功率P的单位选千瓦 (kW),角速度w的单位选弧度/秒(1s),注意 w=2πnl/60,其中n为转速(转/分),则有 M。=9549 外力偶矩M的方向: n 主动轮M与n方向一致,从动轮M。与n方向相反
第三节 外力偶矩 扭矩和扭矩图 1. 扭转的外力偶矩 功率等于力偶矩乘以角速度,功率P的单位选千瓦 (kW),角速度ω的单位选弧度/秒(1/s),注意 ω=2πn/60,其中n为转速(转/分),则有 外力偶矩Me的方向: 主动轮Me与n方向一致,从动轮Me与n方向相反。 n P Me = 9549 B A a a C n d