
弟)草AWUN后坦下时数子群调 为导出一种计算相干解调器误码特性的通用算法,先讨论BPSK调制的误码率特T 性。 ()BPSK信号的解调ML判决及其误码特性 假定两种符号等概出现,采用相干解调器输出的符号矢量分别为:了=√E,+)或 -√E。+n:则随机变量的条件PDF为: p(vlv=v0))=- 1 -exp- (5-2-1a N。 p(vlv=v)= p 1 (5-2-1b) N。 该PDF的形状如图5-2-2所示。 di =2.Es v(o)o v 图5-2-1BPSK的符号星座点 p(ilv=v) p(ilv=v") √E E 图5-2-2BPSK接收符号失量的PDI ■对于一个接收符号矢量,令=代入上式,可知基于ML准则的符号判决规则可 简化为:当>0时,判为v0:当立<0时,判为v©。 ■这个判决准则,本质上也是二维空间中的欧氏距离最小准则,只不过是因为星座点 都在实轴上而只取实部的值。在发送v)时,错误概率就是<0的概率,即: P(elv)=[p(vl)d=- Ht- 1 N。 (5-2-2a 西安电子科技大学
第 5 章 AWGN信道下的数字解调 西安电子科技大学 11 为导出一种计算相干解调器误码特性的通用算法,先讨论 BPSK 调制的误码率特 性。 (1) BPSK 信号的解调 ML 判决及其误码特性 假定两种符号等概出现,采用相干解调器输出的符号矢量分别为: v% = + Eb h 或 - + Eb h ;则随机变量 v% 的条件 PDF 为: 2 (0) 0 0 1 | | ( | ) exp[ ] Eb p p N N + = = - v v v v % % (5-2-1a) 2 (1) 0 0 1 | | ( | ) exp[ ] Eb p p N N - = = - v v v v % % (5-2-1b) 该 PDF 的形状如图 5-2-2 所示。 ● (0) v ● (1) v 0 12 2 b d E = 图 5-2-1 BPSK 的符号星座点 - Eb Eb v% (1) (0) p(v% | ) v v = p(v% | ) v v = 图 5-2-2 BPSK 接收符号矢量的 PDF n 对于一个接收符号矢量 vˆ ,令 v% = vˆ 代入上式,可知基于 ML 准则的符号判决规则可 简化为:当 vˆ > 0 时,判为 (1) v ;当 vˆ < 0 时,判为 (0) v 。 n 这个判决准则,本质上也是二维空间中的欧氏距离最小准则,只不过是因为星座点 都在实轴上而只取 vˆ 实部的值。在发送 (1) v 时,错误概率就是 v% < 0 的概率,即: 2 0 0 (1) (1) 0 0 1 ( ) ( | ) ( | ) exp[ ] Eb P e p d d -• p N -• N - = = - Ú Ú v v v v v v % % % % (5-2-2a)
男草AwUN坦下的数子群网 =左xh=026 其中Q(x)为标准高斯的截尾误差函数。同理在发送v时的错误概率就是氵>0的概率 为: P(elv))=(2E/No) (5-2-2b) 因为v和v是等概发送的,因此平均错误概率为: P.P(elv)/2+P(el v))/2 =(2E,INo) (5-2-3a) 错误概率只与解调器输出的比特信噪比E。/N。有关,而与信号和噪声的其他细节特征无 关。上式错误概率也可用信号的欧氏距离(d。,=2√E,)表示为: B=2N)) (5-23b) MPAM比特误码曲线 202224 Eb/NO(dB) 图5-23MPAM调制的比特误码特性 ◆BPSK可看作是M-2的MPAM,其误码特性如图52-3中M=2的曲线所示。 ◆BSK相干解调中存在0/π相位模糊的问题,即输出的特征矢量Y中是否因载波 相偏引入了π的相位移而使?出现正负值反转的现象,而反转前后的值都是 BPSK符号的有效取值,因而不能对是否有反转做出识别。 西安电子科技大学
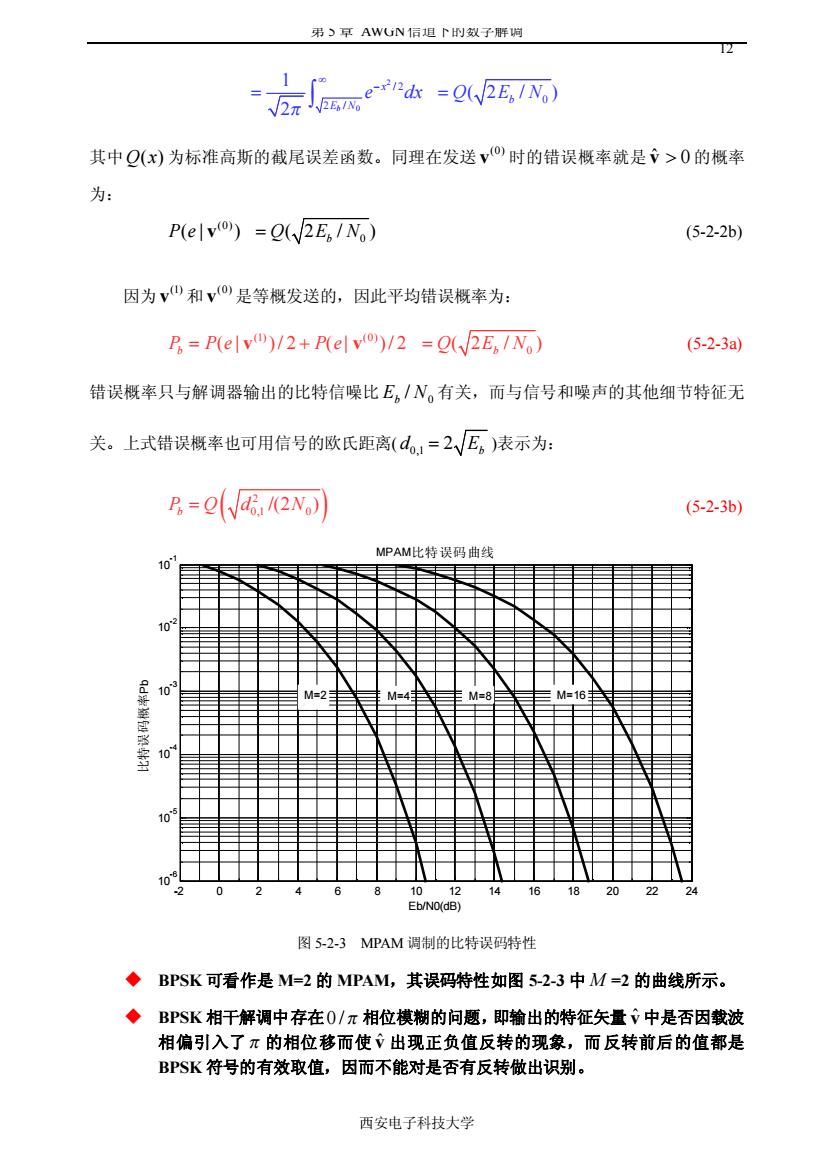
第 5 章 AWGN信道下的数字解调 西安电子科技大学 12 2 0 / 2 2 / 1 2 b x E N e dx p • - = Ú 0 ( 2 / ) Q E N b = 其中Q x( ) 为标准高斯的截尾误差函数。同理在发送 (0) v 时的错误概率就是 vˆ > 0 的概率 为: (0) P e( | ) v 0 ( 2 / ) Q E N b = (5-2-2b) 因为 (1) v 和 (0) v 是等概发送的,因此平均错误概率为: (1) (0) ( | )/ 2 ( | )/ 2 Pb = + P e v v P e 0 ( 2 / ) Q E N b = (5-2-3a) 错误概率只与解调器输出的比特信噪比 0 / E N b 有关,而与信号和噪声的其他细节特征无 关。上式错误概率也可用信号的欧氏距离( 0,1 d 2 = Eb )表示为: ( ) 2 0,1 0 /(2 ) Pb = Q d N (5-2-3b) -2 0 2 4 6 8 10 12 14 16 18 20 22 24 10-6 10-5 10-4 10-3 10-2 10-1 Eb/N0(dB) 比特 误 码概率Pb MPAM比特误码曲线 M=2 M=4 M=8 M=16 图 5-2-3 MPAM 调制的比特误码特性 u BPSK 可看作是 M=2 的 MPAM,其误码特性如图 5-2-3 中 M =2 的曲线所示。 u BPSK 相干解调中存在0 /p 相位模糊的问题,即输出的特征矢量 vˆ 中是否因载波 相偏引入了p 的相位移而使 vˆ 出现正负值反转的现象,而反转前后的值都是 BPSK 符号的有效取值,因而不能对是否有反转做出识别