弟)草AWUN后坦卜的数子群调 第5章AWGN信道下的数字解调 主要内容 ■数字信号基带解调及符号判决 ■无记亿调制的误码特性 ■数字调制的性能比较 ■CPM信号的解调与检测 5.1数字解调的分解描述 ) 符号判洗 e-ion6) 符号空时同步△x符 载被恢复 △e 步误差估计 △0 载被解调一 基带解圆 一符号判淡一 图51-】数字解调的基本结构框图 5.1.1载波解调 设数字调制信号通过AWGN信道后带通形式的接收信号r()与发送信号s()的关系: ()=s()+n()=Re[s,()n() (61-1a) 其中0。和Q。分别为调制载波的角频率与初始相位:7()为信道引入的带限高斯白噪声: (1)载波解调 所谓载波解调,就是采用与接收信号r()中的载波近似同频同相的正弦波eau4d)作 为本地振荡,对接收信号进行正交下变频,以得到发射信号等效低通信号s,()的估计 s,(t): s0=r0e城门M0=r).ear城Mt-dt 61-2) >)是一个低通滤波器的单位冲激响应,其带宽稍宽于s,()的正频率频带,以 确保滤波时不使有用信号失真,同时滤除带外的噪声: 西安电子科技大学
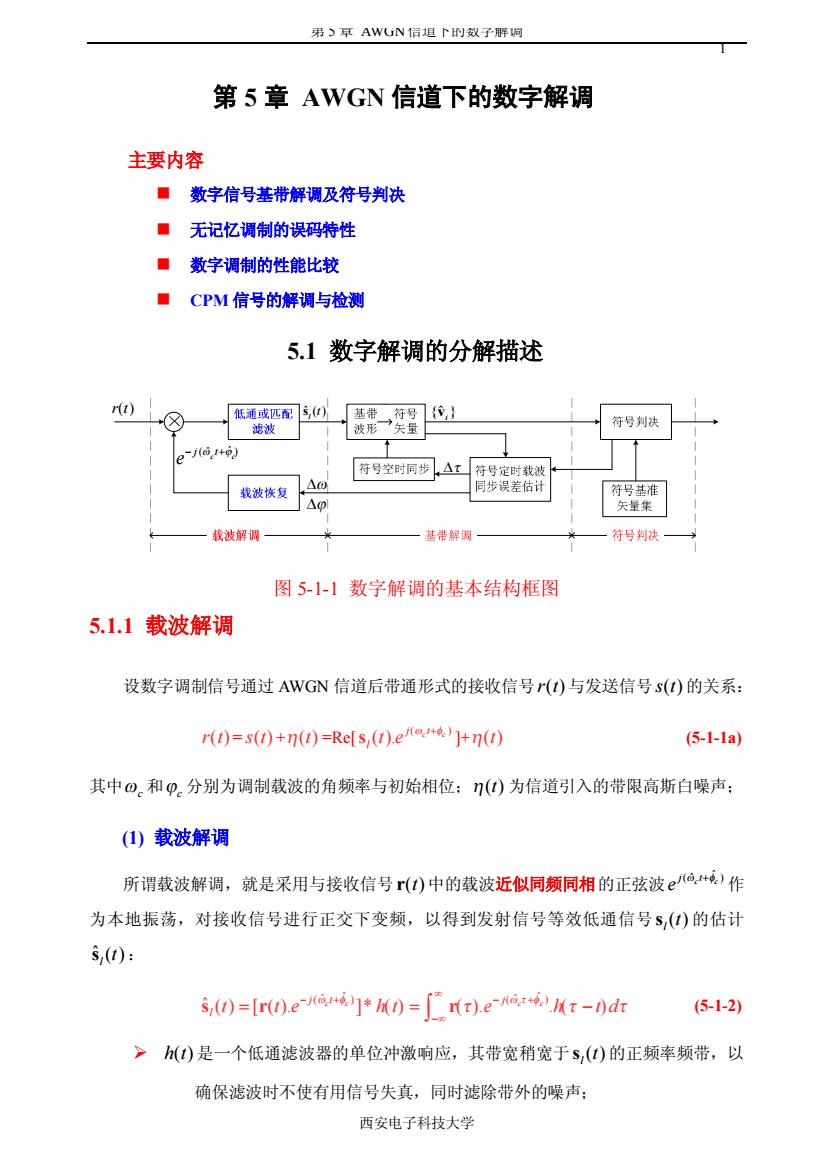
第 5 章 AWGN信道下的数字解调 西安电子科技大学 1 第 5 章 AWGN 信道下的数字解调 主要内容 n 数字信号基带解调及符号判决 n 无记忆调制的误码特性 n 数字调制的性能比较 n CPM 信号的解调与检测 5.1 数字解调的分解描述 r t( ) ˆ ( ) l s t { } ˆ i v Dt Dw Dj ( ) ˆ ˆ c c j t e - + w j 图 5-1-1 数字解调的基本结构框图 5.1.1 载波解调 设数字调制信号通过 AWGN 信道后带通形式的接收信号r t( ) 与发送信号s t( ) 的关系: r t( ) = s t( ) +h( )t =Re[ ( ) ( ). c c j t l t e w f+ s ]+h( )t (5-1-1a) 其中wc 和jc 分别为调制载波的角频率与初始相位;h( )t 为信道引入的带限高斯白噪声; (1) 载波解调 所谓载波解调,就是采用与接收信号r( )t 中的载波近似同频同相的正弦波 ˆ ( ) ˆ c c j t e w f+ 作 为本地振荡,对接收信号进行正交下变频,以得到发射信号等效低通信号 ( ) l s t 的估计 ˆ ( ) l s t : ˆ ˆ ( ˆ ) ( ) ˆ ˆ ( ) [ ( ). ]* ( ) ( ). . ( ) c c c c j t j l t t e h t e h t d w f w t f t t t • - + - + -• = = - Ú s r r (5-1-2) ÿ h t( ) 是一个低通滤波器的单位冲激响应,其带宽稍宽于 ( ) l s t 的正频率频带,以 确保滤波时不使有用信号失真,同时滤除带外的噪声;
)草AWUN坦卜的数子群网 >()也可采用匹配滤波器,以便使输出信号的信噪比提高, ↓本地振荡e6r+,)中的角频率估值0。与初始相位,一般采用下章介绍的载波 同步跟踪技术从接收信号中恢复得到。 集当本地振荡的瞬时相位完全跟踪调制信号中隐含载波的瞬时相位时,二者发生同 频同相的相干现象而能实现完全的载波解调:其输出信号是发送信号等效低通信 号(即复包络)的无偏估计$,(),它是排除了载波频偏与相偏的影响的正确估计。 这就是所谓相干载波解调。 e+ r() +☒ )sQ (a)复数形式 cos(+6) →hM0Re,( r() VCO sin(o1+克) Im(s,(t)) →htH b)实数形式 图5-1-2正交下变频器 (2)零中频信号 如果将正交下变频器中的本地振荡e,d改为ew),其中的o只是标称值等于 0。,而实际上存在频率偏差0,=0。~0。(简称频偏)和相位偏差p,=中-。(简称相偏): 那么正交下变频器的输出就不是s,()的正确估值,而被称为零中频信号,表示为r,(), 即 (t)=[r(t).e-1)dr (6-1-3) 这时正交下变频实现的就不是完全的载波解调。 若要实现完全的载波解调,还需要进一步纠正频偏与相偏,即 s,()=,(0eo,es) (5-14) 西安电子科技大学
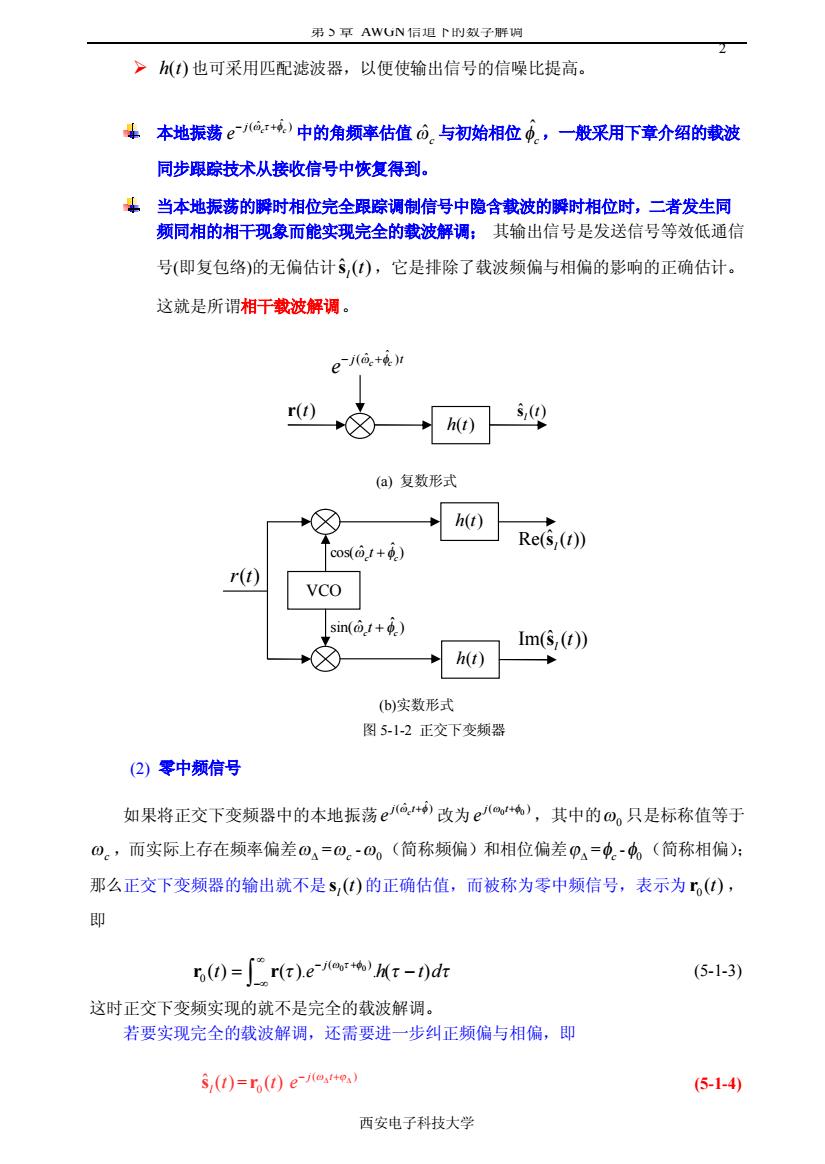
第 5 章 AWGN信道下的数字解调 西安电子科技大学 2 ÿ h t( ) 也可采用匹配滤波器,以便使输出信号的信噪比提高。 本地振荡 ˆ ( ) ˆ c c j e - + w t f 中的角频率估值 ˆwc 与初始相位 ˆfc ,一般采用下章介绍的载波 同步跟踪技术从接收信号中恢复得到。 当本地振荡的瞬时相位完全跟踪调制信号中隐含载波的瞬时相位时,二者发生同 频同相的相干现象而能实现完全的载波解调; 其输出信号是发送信号等效低通信 号(即复包络)的无偏估计ˆ ( ) l s t ,它是排除了载波频偏与相偏的影响的正确估计。 这就是所谓相干载波解调。 (a) 复数形式 (b)实数形式 图 5-1-2 正交下变频器 (2) 零中频信号 如果将正交下变频器中的本地振荡 ˆ ( ) ˆ c j t e w f+ 改为 0 0 j t ( ) e w f+ ,其中的w0 只是标称值等于 wc ,而实际上存在频率偏差wD =wc -w0(简称频偏)和相位偏差jD =fc -f0(简称相偏); 那么正交下变频器的输出就不是 ( ) l s t 的正确估值,而被称为零中频信号,表示为 0 r ( )t , 即 0 0 ( ) 0 ( ) ( ). . ( ) j t e h t d w t f t t t • - + -• = - Ú r r (5-1-3) 这时正交下变频实现的就不是完全的载波解调。 若要实现完全的载波解调,还需要进一步纠正频偏与相偏,即 ˆ ( ) l s t = 0 r ( )t j t ( ) e - + w j D D (5-1-4) VCO ˆ cos( ) ˆ c c w f t + ˆ sin( ) ˆ c c w f t + h t( ) h t( ) Re(ˆ ( )) l s t Im(ˆ ( )) l s t r t( ) h t( ) ˆ ( ) l s t ˆ ( ) ˆ c c j t e - + w f r( )t

弟)草AWUN后坦下的数子群调 ◆可以看出,在通过正交下变频估计基带复信号s,()时,载波的相位偏差P、以 及因载波的颜偏随时间推移而积累的相位移@,1,都直接加入到基带复信号的相 角值之中了,必须纠正这两种偏差才能得到$,()的正确相位角值。 ◆零中频信号可以采用较低的采样率离散化和数字化,因而有利于降低计算和处理 设备的复杂度;处理零中频信号可以达到与直接处理非零中频信号相似的效果, 载波同步跟踪也可以基于零中须接收信号进行。 (③)正交下变频等价于正交投影 对于实的接收信号(),正交下变频器在1时刻输出的等效低通信号估值为 s,(=r())+i"u小h (5-1-5) 其中”)=cos(⑥)h1-t')、f)=sin(⑥,1)h-1)是相互正交的两个波形函数。 因此,上述正交下变频可以看作是将接收信号r()向这个正交基函数族{”):公()) 的投影。 5.1.2基带解调 ◆基带解调就是将载波解调所得等效低通信号的估计$,()映射为符号矢量序列的过程。 ◆对于无记忆调制基带调制,因波形成形方法不同,有以下三种不同的基带解调方法。 ⑧ 0贤一程创 符号判决 复A 0 我波解词 基带解调 一符号判决 (①)符号间隔抽样法 如果发射端采用的是符合奈奎斯特第一准则的成形波g(),那么基带信号波形$,()向 符号矢量的映射方法是,在每个符号间隔中点处对它抽样,即 v,=s,()儿lem i=.,-1,0,1,2 (5-1-6a) 就完成了基带解调。所得特征矢量氵,其实只是一个复数值,看作是二维矢量,它是与第个 发送符号星座点相对应的。 西安电子科技大学
第 5 章 AWGN信道下的数字解调 西安电子科技大学 3 u 可以看出,在通过正交下变频估计基带复信号 ˆ ( ) l s t 时,载波的相位偏差jD 以 及因载波的频偏随时间推移而积累的相位移w t D ,都直接加入到基带复信号的相 角值之中了,必须纠正这两种偏差才 能得到 ˆ ( ) l s t 的正确相位角值。 u 零中频信号可以采用较 低的采样率离散化和数字化,因而有利于降低计算和处理 设备的复杂度;处理零中频信号可以达到与直接处理非零中频信号相似的效果, 载波同步跟踪也可以基于零中频接收信号进行。 (3) 正交下变频等价于正交投影 对于实的接收信号r t( ) ,正交下变频器在t ' 时刻输出的等效低通信号估值为: ˆ ( ') l s t = ( ') ( ') 1 2 ( ).[ ( ) ( )] t t t f t jf t dt • -• + Ú r (5-1-5) 其中 ( ') 1 ( ) cos( ˆ ). ( ') t c f t = - w t h t t 、 ( ') 1 ( ) sin( ˆ ). ( ') t c f t = - w t h t t 是相互正交的两个波形函数。 因此,上述正交下变频可以看作是将接收信号r( )t 向这个正交基函数族{ ( ') 1 ( ) t f t ; ( ') 2 ( ) t f t } 的投影。 5.1.2 基带解调 u 基带解调就是将载波解调所得等效低通信号的估计ˆ ( ) l s t 映射为符号矢量序列的过程。 u 对于无记忆调制基带调制, 因波形成形方法不同,有以下三种不同的基带解调方法。 r t( ) ˆ ( ) l s t { } ˆ i v Dt Dw Dj ( ) ˆ ˆ c c j t e - + w j (1) 符号间隔抽样法 如果发射端采用的是符合奈奎斯特第一准则的成形波 g t( ),那么基带信号波形ˆ ( ) l s t 向 符号矢量的映射方法是,在每个符号间隔中点处对它抽样,即 ˆ i v ˆ ( ) | l t iT t = = s i = - ., 1,0,1,2,. (5-1-6a) 就完成了基带解调。所得特征矢量 ˆ i v 其实只是一个复数值,看作是二维矢量,它是与第i 个 发送符号星座点相对应的

)草AWUN坦卜的数子群网 (2)符号间隔积分法 ■如果发射端采用的是符合奈奎斯特第三准则的成形波g(),那么基带信号波形 $,()向符号矢量的映射方法是,在每个符号间隔分别对其实部和虚部进行积分: =0h-i0h+小@oh 617 即就完成了基带解调。 ■如果成形波g(t)是属于奈奎斯特第二准则的,那么先要分别对$,()的实部和虚部 进行基于限幅电平A的矩形脉冲化处理,再进行符号间隔积分,即 =0h+aoh (5-1-8a) 其中 70=gm70A0i0北00=5gg0A4g0B6 001,(0k4A0 009)k4A0 (③)相关解调法 ·基于单一成形波调制信号的相关解调 如果发射端的调制方式是基于单个成形波g)的,并且g)是平移正交的,即 {g(1-iT):i=,-1,0,1,2.}是一个正交基函数族,例如g()为平方根升余弦谱特性的: 那么这种实现基带解调的映射就是内积空间的投影(即相关)运算,第ì个符号矢量的估计 为: ,=s0g1-iTdi=-10,12 (5-1-9) ◆这种相关运算可以在基于(5-12)式的正交下变频器中直接实现:将其中的低通滤 波器()取代为匹配滤波器g(),然后将其输出信号$,()在每个符号间隔中点 抽一个样点,即实现了基带解调。 ·M元正交波形调制信号的相关解调 ①非相干解调 将()分别与{m()}中各个波形进行相关(即内积)运算得到M个相关量:即 m)-H)/)d m=0,1,2.,M-1 (6-1-10a) 西安电子科技大学
第 5 章 AWGN信道下的数字解调 西安电子科技大学 4 (2) 符号间隔积分法 n 如果发射端采用的是符合奈奎斯特第三准则的成形波 g t( ) ,那么基带信号波形 ˆ ( ) l s t 向符号矢量的映射方法是,在每个符号间隔分别对其实部和虚部进行积分: ˆ i v / 2 / 2 ˆ ( ) iT T l iT T t dt + - = Ú s / 2 / 2 ˆ ( ) iT T l iT T I t dt + - = Ú + / 2 / 2 ˆ ( ) iT T l iT T j Q t dt + Ú - (5-1-7) 即就完成了基带解调。 n 如果成形波 g t( )是属于奈奎斯特第二准则的,那么先要分别对ˆ ( ) l s t 的实部和虚部 进行基于限幅电平 A 的矩形脉冲化处理,再进行符号间隔积分,即 ˆ i v / 2 / 2 ( ) iT T l iT T I t dt + - = Ú + / 2 / 2 ( ) iT T l iT T j Q t dt + Ú - (5-1-8a) 其中 ˆ ˆ ( ( )) (| ( )| ) ( ) ˆ 0 (| ( )| ) l l l l sgn I t A I t A I t I t A ÏÔ ³ = Ì ÔÓ < ˆ ˆ ( ( )) (| ( )| ) ( ) ˆ 0 (| ( )| ) l l l l sgn Q t A Q t A Q t Q t A ÏÔ ³ = Ì Ô < Ó (5-1-8b) (3) 相关解调法 l 基于单一成形波调制信号的相关解调 如果发射端的调制方式是基于单个成形波 g t( ) 的,并且 g t( ) 是平移正交的,即 { g( ) t - iT ;i = - ., 1,0,1,2,. }是一个正交基函数族,例如 g t( )为平方根升余弦谱特性的; 那么这种实现基带解调的映射就是内积空间的投影(即相关)运算,第i 个符号矢量的估计 为: ˆ i v ˆ ( ). ( ) l t g t iT dt • -• = - Ú s i = - ., 1,0,1,2,. (5-1-9) u 这种相关运算可以在基于(5-1-2)式的正交下变频器中直接实现;将其中的低通滤 波器 h t( ) 取代为匹配滤波器 g t( ) ,然后将其输出信号 ˆ ( ) l s t 在每个符号间隔中点 抽一个样点,即实现了基带解调。 l M 元正交波形调制信号的相关解调 ①非相干解调 将 0 r ( )t 分别与{ ( ) m f t }中各个波形进行相关(即内积)运算得到M 个相关量;即 vˆ( ) m = / 2 0 / 2 ( ). ( ) T m T t iT f t dt - + Ú r m M = - 0,1,2,., 1 (5-1-10a)
弟)草AWUN信坦下时数子群调 这些相关量都是复数,可以取其幅度作为符号判决量,即 Ro=lVE,+nol:R=m:m=12.M-1 (5-1-10c) 其中(1}是一个实部虚部的均值都为0,实部虚部的方差都为N。/2的复高斯随机变量。 判决时比较这M个相关幅度值的大小,如果其中R的值最大就判为第m种符号,即 m=坚M-m (61-10d) 6() +☒ ( 60 至检测器, (× 图5-1-3M元正交调制信号的相关解调 ②相干解调 当然,M元正交波形调制也是可以利用相位信息来改善误码特性的,但这时必须采 用相干载波解调所得等效低通信号$,()代替零中频信号。()进行基带解调,即 v(m)-s(T)f.(dt m=01,2,M-1 (5-1-11a) 并取相关量的实部而不是幅度作为符号判决量,即 元n=Re[(m)j m=0,1,2,M-1 (6-1-11b) 判决时只要这M个相关量实部值的大小,如果其中元。的值最大,就将它判为第m种 符号:其数学表达就是 Relv(m) (5-1-11d 本例中m0。这就是M元正交波形调制信号的相干解调判决。 >这里取相关量的实部作为判决量,是因为发送端进行M元正交波形基带调制时所产 生的预包络信号s,()只有实部,没有虚部:接收端基于相干载波解调所得$,()中的 有用信号部分也应该只有实部,因此取相关量的实部不降低有用信号功率却甩掉了 虚部噪声,使其信噪比提高一倍,误码特性可改善3B:这就是相干解调利用相位信 西安电子科技大学
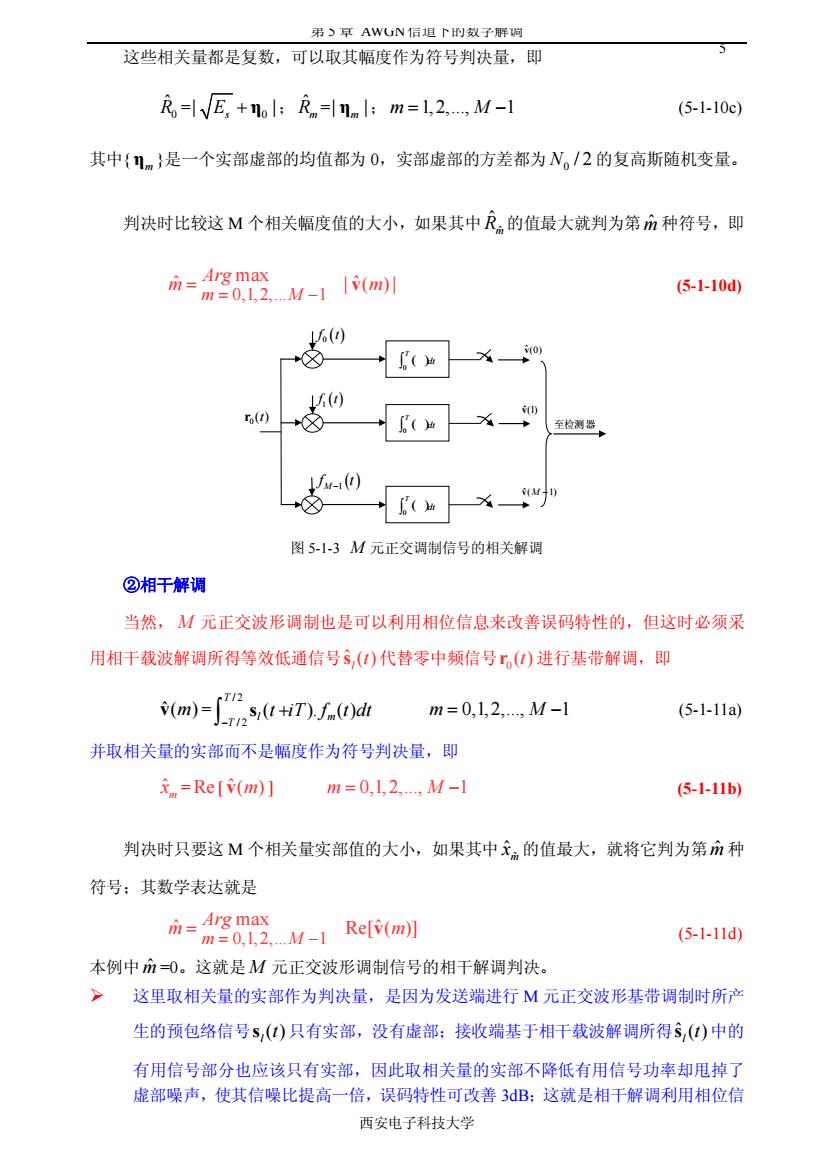
第 5 章 AWGN信道下的数字解调 西安电子科技大学 5 这些相关量都是复数,可以取其幅度作为符号判决量,即 0 Rˆ = 0 | | Es + η ; ˆRm =| | ηm ; m M = - 1,2,., 1 (5-1-10c) 其中{ηm }是一个实部虚部的均值都为 0,实部虚部的方差都为 0 N / 2 的复高斯随机变量。 判决时比较这 M 个相关幅度值的大小,如果其中 ˆ ˆRm 的值最大就判为第mˆ 种符号,即 0,1, 2,. 1 max ˆ | (ˆ ) | m M Arg m m = - = v (5-1-10d) f t 0 ( ) f t 1 ( ) f t M -1 ( ) ( ) 0 T dt Ú ( ) 0 T dt Ú ( ) 0 T dt Ú vˆ(0) vˆ(1) vˆ(M -1) 0 至检测器 r ( )t 图 5-1-3 M 元正交调制信号的相关解调 ②相干解调 当然, M 元正交波形调制也是可以利用相位信息来改善误码特性的,但这时必须采 用相干载波解调所得等效低通信号ˆ ( ) l s t 代替零中频信号 0 r ( )t 进行基带解调,即 vˆ( ) m = / 2 / 2 ( ). ( ) T l m T t iT f t dt - + Ú s m M = - 0,1,2,., 1 (5-1-11a) 并取相关量的实部而不是幅度作为符号判决量,即 ˆm x =Re [ vˆ( ) m ] m M = - 0,1,2,., 1 (5-1-11b) 判决时只要这 M 个相关量实部值的大小,如果其中 ˆ ˆm x 的值最大,就将它判为第mˆ 种 符号;其数学表达就是 0,1, 2,. 1 max ˆ Re[ˆ( )] m M Arg m m = - = v (5-1-11d) 本例中mˆ =0。这就是M 元正交波形调制信号的相干解调判决。 ÿ 这里取相关量的实部作为判决量,是因为发送端进行 M 元正交波形基带调制时所产 生的预包络信号 ( ) l s t 只有实部,没有虚部;接收端基于相干载波解调所得ˆ ( ) l s t 中的 有用信号部分也应该只有实部,因此取相关量的实部不降低有用信号功率却甩掉了 虚部噪声,使其信噪比提高一倍,误码特性可改善 3dB;这就是相干解调利用相位信