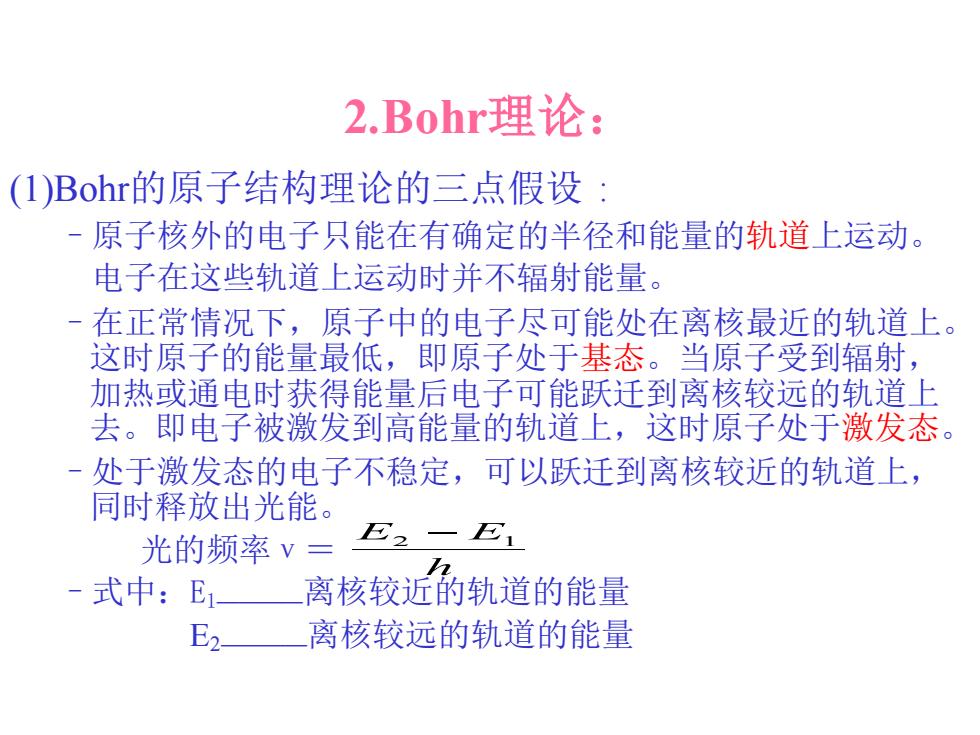
2.Bohr理论: (1)Bohr的原子结构理论的三点假设: -原子核外的电子只能在有确定的半径和能量的轨道上运动。 电子在这些轨道上运动时并不辐射能量。 在正常情况下,原子中的电子尽可能处在离核最近的轨道上。 这时原子的能量最低,即原子处于基态。当原子受到辐射, 加热或通电时获得能量后电子可能跃迁到离核较远的轨道上 去。即电子被激发到高能量的轨道上,这时原子处于激发态。 -处于激发态的电子不稳定,可以跃迁到离核较近的轨道上, 同时释放出光能。 光的频率V= E2一E1 -式中:E 离核较近的轨道的能量 E2 离核较远的轨道的能量
(1)Bohr的原子结构理论的三点假设 : –原子核外的电子只能在有确定的半径和能量的轨道上运动。 电子在这些轨道上运动时并不辐射能量。 –在正常情况下,原子中的电子尽可能处在离核最近的轨道上。 这时原子的能量最低,即原子处于基态。当原子受到辐射, 加热或通电时获得能量后电子可能跃迁到离核较远的轨道上 去。即电子被激发到高能量的轨道上,这时原子处于激发态。 –处于激发态的电子不稳定,可以跃迁到离核较近的轨道上, 同时释放出光能。 光的频率ν= –式中:E1————离核较近的轨道的能量 E2————离核较远的轨道的能量 2.Bohr理论: h E2 − E1

·轨道 ·基态、激发态 。引入量子数一n,1、2、3
• 轨道 • 基态、激发态 • 引入量子数- n , 1 、 2 、3

2.Bohr理论: Bohr在其三点假设的基础上,运用牛顿力学定律 推算出下列关香戎: r=aon E=一 n2 1 KJ.mol-1 v=3.29×1015( n2-n2)s-1 (n1<n2) 式中:r一氢原子轨道的半径,ao=0.053纳米 (玻尔半径) E—氢原子轨道的能量 v一氢原子中电子由高能态跃迁到低能 态时辐射光的平率一正整数(自然数,量 子数)
Bohr在其三点假设的基础上,运用牛顿力学定律 推算出下列关系式: r=a0n 2 E=- KJ.mol-1 ν=3.29╳1015( )s- 1 (n1<n2) 式中:r——氢原子轨道的半径,a0=0.053纳米 (玻尔半径) E——氢原子轨道的能量 ν——氢原子中电子由高能态跃迁到低能 态时辐射光的平率 n——正整数(自然数,量 子数)。 2.Bohr理论: 2 1312 n 2 2 2 1 1 1 n n −

2.Bohr理论: 1 1 ·根据v=3.29X1015( 2 2 )s1 在可见光区: n 当n1=2,n2=3 为Ha谱线的频率 n2=4 为HB谱线的频率 n2=5 为Y谱线的频率 n2=6 为Hδ谱线的频率 在红外光区: 当n1=3,n2=4,5,6,7有一组谱线 在紫外光区: 当n1=3,n2=2,3,4,5也有一组谱线
• 根据ν=3.29╳1015( )s- 1 在可见光区: 当n1 =2, n2 =3 为Hα谱线的频率 n2 =4 为Hβ谱线的频率 n2 =5 为Hγ谱线的频率 n2 =6 为Hδ谱线的频率 在红外光区: 当n1 =3,n2 =4,5,6,7有一组谱线 在紫外光区: 当n1 =3, n2 =2,3,4,5也有一组谱线 2.Bohr理论: 2 2 2 1 n 1 n 1 −

2.Bohr理论: (3)玻尔理论的贡献和局域性: -贡献: ·成功的解释了氢原子光谱。 ·提出了主量子数n和能级的重要概念,为 近代原子结构的发展作出一定的贡献。 -局限性: ·不能说明多电子原子光谱和氢原子光谱的 精细结构; ·不能说明化学键的本质
(3)玻尔理论的贡献和局域性: – 贡献: • 成功的解释了氢原子光谱。 • 提出了主量子数n和能级的重要概念,为 近代原子结构的发展作出一定的贡献。 – 局限性: • 不能说明多电子原子光谱和氢原子光谱的 精细结构; • 不能说明化学键的本质。 2.Bohr理论: