
北京化工大学2010—2011学年第一学期 《高等数学(I)》期末考试试卷 课程代码MAT13900T 班级: 姓名: 学号: 分数: 题号 二 三 四 五 总分 得分 一、填空题(3分×6=18分) *母) 2.由方程xy=1-xe确定的隐函数y=y(x)的导 dy dx 3.设y=cos2x,则y四=」 4.曲线y=Insecx在x=0处的曲率为 5.在yOz面上的曲线y2-z=0绕:轴旋转后的曲面与平面x+z=1的交线在xOy 面上的投影方程为 6.过点(亿2,1,-到且与直线--+ -121 垂直的平面方程为」 二、解下列各题(6分×9=54分)》 1.求过(0,2,4)且与两平面x+2y-2=1和x-y+z=1平行的直线方程。 第1页
第 1 页 北京化工大学 2010——2011 学年第一学期 《高等数学(I)》期末考试试卷 课程代码 M A T 1 3 9 0 0 T 班级: 姓名: 学号: 分数: 题号 一 二 三 四 五 总分 得分 一、填空题(3 分×6 = 18 分) 1.求极限 tan 0 1 lim x x x → + = 。 2.由方程 1 ey x y x = − 确定的隐函数 y y x = ( ) 的导数 d d y x = 。 3.设 2 y x = cos ,则 (n) y = 。 4.曲线 y x = ln sec 在 x = 0 处的曲率为 。 5.在 yOz 面上的曲线 2 y z − = 0 绕 z 轴旋转后的曲面与平面 x z + =1 的交线在 xOy 面上的投影方程为 。 6.过点 (2 ,1, 3 − ) 且与直线 1 1 1 2 1 x y z − + = = − 垂直的平面方程为 。 二、解下列各题(6 分×9 = 54 分) 1.求过 (0 , 2 , 4) 且与两平面 x y z + − = 2 1 和 x y z − + =1 平行的直线方程

2.求函数y=x0ocs2x在x=号处的微分。 x=∫sinu'du 3.设参数方程了 y=f.cosudu 伪参数,求品。 第2页
第 2 页 2.求函数 y x x = cos 2 在 4 x = 处的微分。 3.设参数方程 2 0 2 0 sin d cos d t t x u u y u u = = ,t 为参数,求 2 2 d d y x

4.计算不定积分「cosInxdx 5.计算定积分 第3页
第 3 页 4.计算不定积分 cos ln dx x 5.计算定积分 3 1 1 2 cos d 2 5 4 x x x x x x − + − −
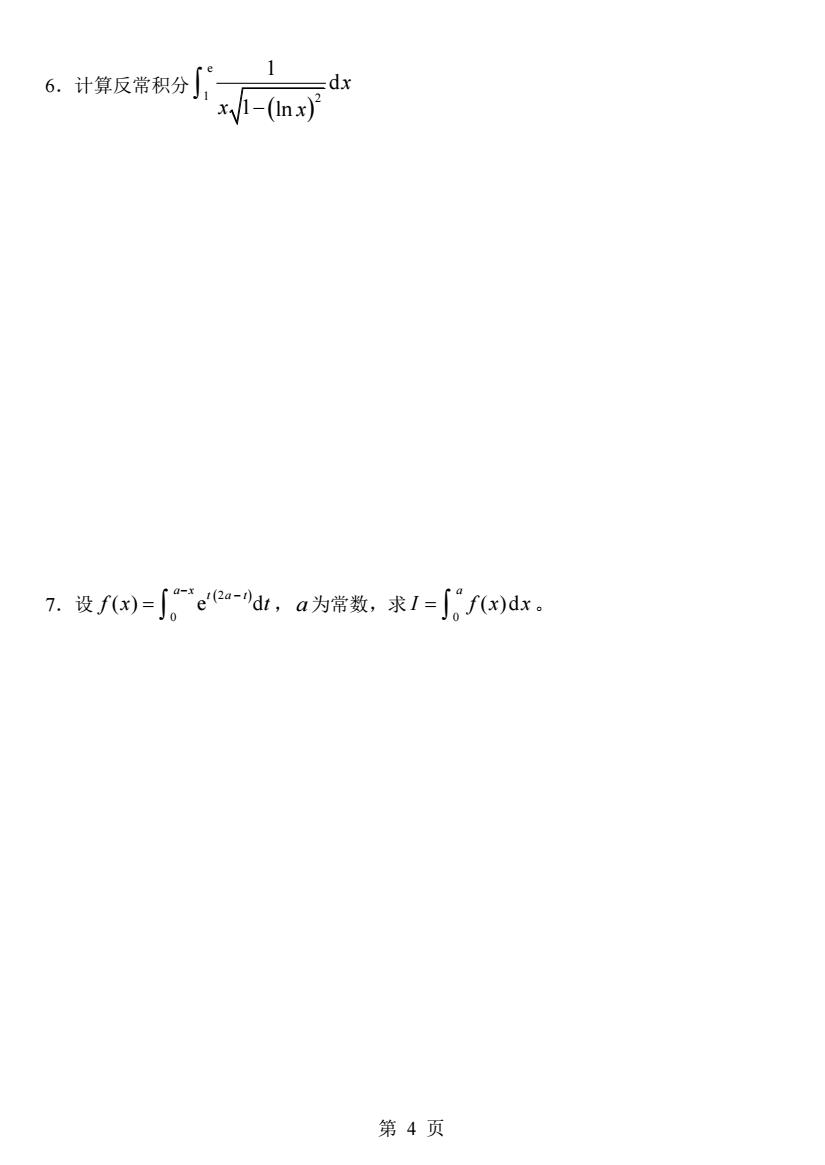
6.计算反常积分」, -dx x1-(Inx) 7.设f(x)=∫ea-d,a为常数,求1=∫fx)dx。 第4页
第 4 页 6.计算反常积分 ( ) e 1 2 1 d 1 ln x x − x 7.设 (2 ) 0 ( ) e d a x t a t f x t − − = , a 为常数,求 0 ( )d a I f x x =

8.求极限网snx子 9.计算p=sin0与p=cos0所围公共部分的面积。 第5页
第 5 页 8.求极限 2 2 2 0 1 cos lim x sin x → x x − 9.计算 = sin 与 = cos 所围公共部分的面积