(一)引例 ◆例1圆柱体的体积 底面半径:r 高: 二元函数 →V=元r27% ◆例2三角形的面积 (1)三边长:a,b,c 三元函数 →S=pVp-ap-b(p-c) P=2a+b+c海伦公试) (2)两边长:4,b色一 三元函数 S=二absinC正弦定理) 2
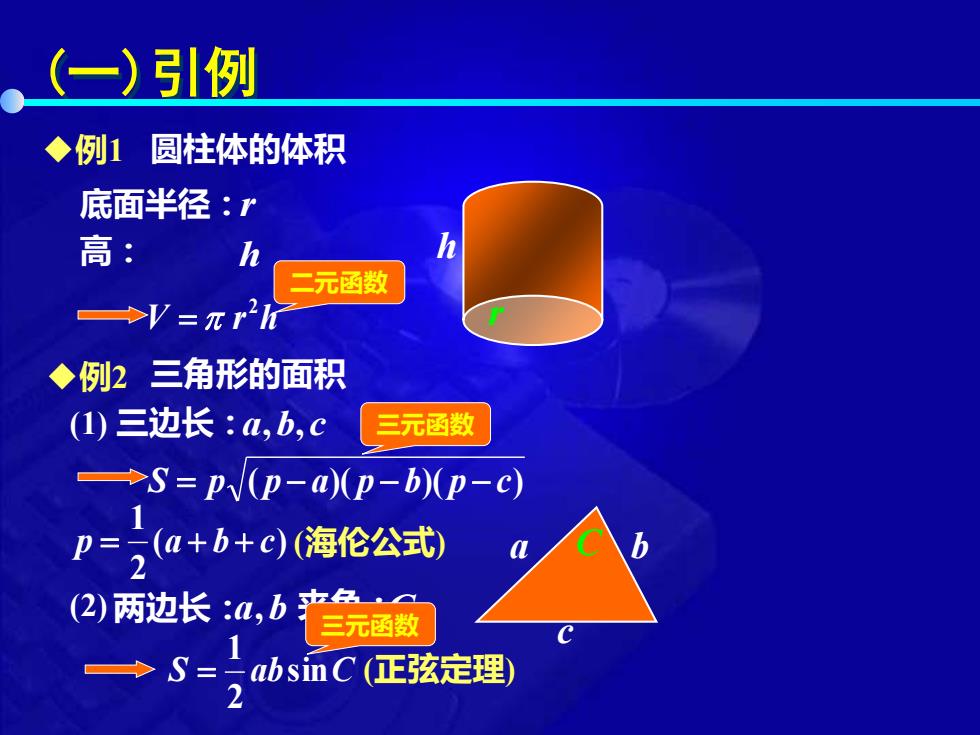
(一)引例 圆柱体的体积 r h 三角形的面积 a b c ◆例1 V r h 2 = 底面半径: r 高: h ◆例2 三边长: a,b,c S = p ( p − a)( p − b)( p − c) ( ) 2 1 p = a + b + c (海伦公式) 两边长: a,b 夹角: C (1) (2) S absinC 2 1 = (正弦定理) C 二元函数 三元函数 三元函数

一、多元函数的概念 (一)引例 (二) 平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义

、多元函数的概念 (一)31例 (二)平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义
(二)平面点集 ◆例1圆柱体的体积 定义域 底面半径:r D,={r,)lr>0,h>0 高: 二元函数 平面点集 →V=元r2 ◆例2三角形的面积 D={(a,b,c)a>0,b>0,c>0 (1)三边长:a,b,c 三元函数 ={(a,b,C)川a>0,b>0,0<C<π →S=p√(p-@(p-b(p-C) 空间点集 P=2a+b+c海伦公试) (2)两边长:a,b品☑ 三元函数 S=二absinC正弦定理) 2
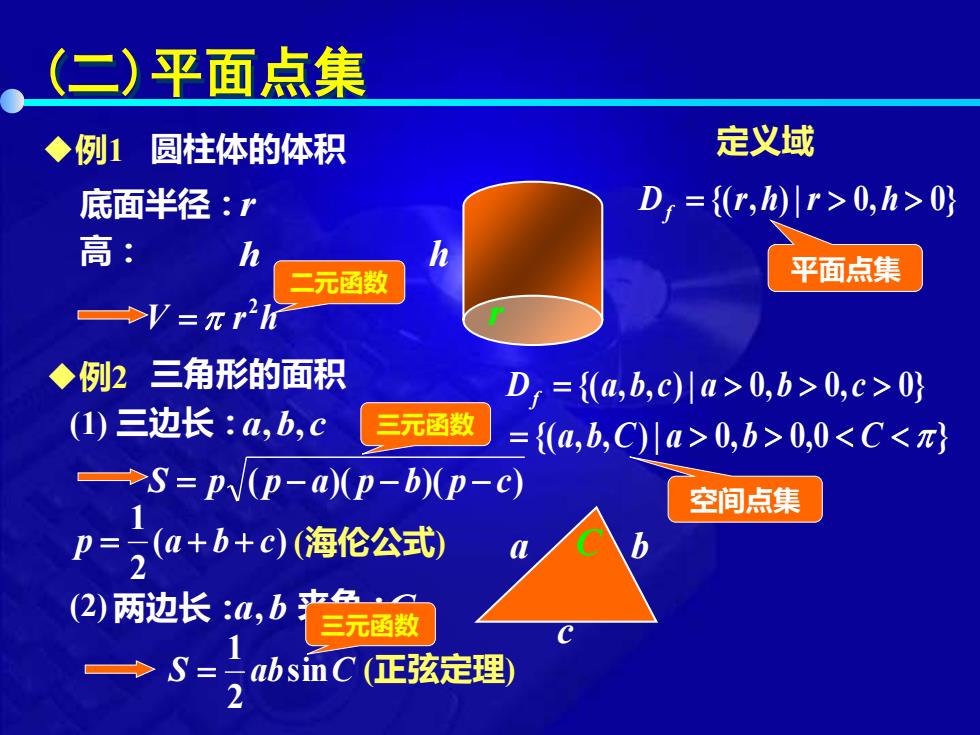
(二)平面点集 圆柱体的体积 r h 三角形的面积 a b c ◆例1 V r h 2 = 底面半径: r 高: h ◆例2 三边长: a,b,c S = p ( p − a)( p − b)( p − c) ( ) 2 1 p = a + b + c (海伦公式) 两边长: a,b 夹角: C (1) (2) S absinC 2 1 = (正弦定理) C 定义域 D = {(r,h)|r 0,h 0} f D = {(a,b,c)| a 0,b 0,c 0} f = {(a,b,C)| a 0,b 0,0 C } 平面点集 空间点集 二元函数 三元函数 三元函数

>平面点集的有关概念 二维空间: 二元有序实数组(ky)的全体,即:{(x,y)川x∈R,y∈R 记作:R或RxR ●注 (1)二维空间的几何意义一坐标平面 (2)二维空间的元素一P=(x,y) 坐标平面内的点 平面点集: 二维空间的任一子集,记作:ECR ●注 平面点集通常是坐标平面上具有某种性质的点的集合, 记作E={化,y)(,y)具有性质P
➢平面点集的有关概念 二维空间: 二元有序实数组(x,y)的全体, 即: 记作: ⚫注 二维空间的几何意义—坐标平面 二维空间的元素— P x y = ( , ) 坐标平面内的点 平面点集: 二维空间的任一子集, 记作: 平面点集E通常是坐标平面上具有某种性质的点的集合, 记作:E={(x,y)|(x,y)具有性质P} (1) (2) {( x, y)| x R, y R} 2 E R ⚫注 或 R R 2 R